数据结构第三遍补充（图的应用）-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构第三遍补充（图的应用）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一. Kruskal算法

Kruskal算法实现的关键是:当一条边加入到TE的集合后，如何判断是否构成回路?
答：简单的解决方法是:定义一个一维数组Vset[n]; 存放图T中每个顶点所在的连通分量的编号。
① 初值: Vset[i]=i, 表示每个顶点各自组成一个连通分量，连通分量的编号简单地使用顶点在图中的位置(编号)。
② 当往T中增加一条边(Vi, Vj) 时，先检查Vset[i]和Vset[j]值:
a 若Vset[i]=Vset[j]: 表明vi和vj处在同一个连通分量中，加入此边会形成回路;
b 若Vset[i]≠Vset[j]:则加入此边不会形成回路，将此边加入到生成树的边集中。
③加入一条新边后，将两个不同的连通分量合并，将一个连通分量的编号换成另一个连通分量的编号。

算法实现

MSTEdge *Kruskal MST(ELGraph *G)
/*用Kruskal算法构造图G的最小生成树*/
{  MSTEdge TE[ ;
   int  j, k, V, s1, s2, Vset[] ;
  WeightType w ;
  Vset=(int *)malloc(G->vexnum *sizeof(int)) ;
  for (=0; j<G->vexnum; j++)
     Vset[j]=j ; /* 初始化数组Vset[n] */
     sort(G->edgelist); /* 对表按权值从小到大排序*/
   j=0 ;k=0;
   while (k<G->vexnum-1 &&j< G->edgenum)
     { s1=Vset[G->edgelist[j].vex1];
       s2= Vset[G->edgelist[j].vex2] ;
     /*若边的两个顶点的连通分量编号不同，边加入到TE中*/
      if (s1!=s2)
       { TE[k].vex 1=G->edgelist[j].vex1 ;
         TE[k].vex2=G->edgelist[j].vex2 ;
         TE[k].weight=G->edgelis t[j].weight;
        for (v=0; v<G->vexnum; v++)
            if (Vset[v]= =s2) Vset[v]=s1 ;
      }
     j++ ;
   }
   free(Vset) ;
  return(TE) ;}
/*求最小生成树的Kruskal算法*/

算法分析:
设带权连通图有n个顶点，e条边，则算法的主要执行是:
① Vset数组初始化: 时间复杂度是O(n) ;
② 边表按权值排序: 若采用堆排序或快速排序，时间复杂度是O(eloge) ;
③ while循环:最大执行频度是O(n),其中包含修改Vset数组，共执行n-1次，时间复杂度是0(n2) ;
整个算法的时间复杂度是O(eloge+n2)。

二.拓扑排序

定义
（1）拓扑排序(Topological Sort) : 由某个集合上的一个偏序得到该集合上的一个全序的操作。
① 集合上的关系:集合A上的关系是从A到A的关系(AxA)
② 关系的自反性:若Va∈A有(a, a)∈R,称集合A上的关系R是自反的。
③关系的对称性:如果对于a, b∈A，只要有(a,b)∈R就有(b, a)∈R ，称集合A上的关系R是对称的
④ 关系的对称性与反对称性:如果对于a, b∈A ，只要有(a, b)∈R就有(b, a)∈R ，称集合A上的关系R
是对称的。如果对于a, b∈A，仅当a=b时有(a,b)∈R和(b, a)∈R ，称集合A上的关系R是反对称的。
⑤关系的传递性:若a, b, c∈A,若(a， b)∈R, 并且(b, c)∈R, 则(a, c)∈R ，称集合A上的关系R是传递的。
⑥ 偏序:若集合A上的关系R是自反的，反对称的和传递的，则称R是集合A上的偏序关系。
⑦ 全序:设R是集合A上的偏序关系，Va, b∈A，必有aRb或bRa，称R是集合A上的全序关系。
即偏序是指集合中仅有部分元素之间可以比较，而全序是指集合中任意两个元素之间都可以比较。
在AOV网中，若有有向边<i,j>,则i是j的直接前驱，j是的直接后继;推而广之，若从顶点i到顶点j有有向路径，则i是j的前驱，j是i的后继。
在AOV网中，不能有环，否则，某项活动能否进行是以自身的完成作为前提条件。
检查方法:对有向图的顶点进行拓扑排序，若所有顶点都在其拓扑有序序列中，则无环。
向图的拓扑排序:构造AOV 网中顶点的一个拓扑线性序列(v’1,V’2, …,v’n),使得该线性序列不仅保持有向图中顶点之间的优先关系，而且对原图中没有优先关系的顶点之间也建立-种(人为的)优先关系。
手工实现
如图是一个有向图的拓扑排序过程，其拓扑序
列是: (V1,V6,V4,V3;V2,Vs)
算法思想
◆ 采用正邻接链作为AOV网的存储结构;
◆ 设立堆栈，用来暂存入度为0的顶点;
◆ 删除顶点以它为尾的弧:弧头顶点的入度减1。
算法实现
(1)统计各顶点入度的函数

void count indegree(ALGraph *G)
{ int k ; 
  LinkNode *p ;
  for (k=0; k<G->vexnum; k++)
     G-> adjlist[kJ.indegree=0; /*顶点入度初始化*/
  for (k=0; k<G->vexnum; k++)
   { p=G-> adjlist[k].firstarc ;
      while (p!=NULL)/*顶点入度统计*/
      { G->adjlist[p->adjvex].indegree++ ;
         p=p-> nextarc ;
      }
   }
 }

(2)拓扑排序算法

int Topologic Sort(ALGraph *G, int topol[)
/*顶点的拓扑序列保存在一维数组topol中 */
{  int k, no, vex_ no, top=0, count =0，boolean=1 ;
   int stack[MAX_ VEX] ;  /*用作堆栈*/
   LinkNode *p ; 
   count_ indegree(G); /* 统计各顶点的入度*/
   for (k=0; k<G->vexnum; k++)
     if (G->adjJist[k].indegree--0)
          stack[+ +top]=G-> adjlist[k].data ;
    do{if(top==0) boolean=0 ;
    else
     { no=stack[top-] ;/*栈顶元素出栈*/
       topl[++count]=no; /* 记录顶点序列*/
        p=G-> adjlist[no].firstarc ;
       while (p!=NULL) /* 删除以顶点为尾的弧*/
         { vex_ no=p->adjvex ;
           G-> adjlist[vex no]indegree--;
           if (G->adjlist[vex no].indegree==0)
              stack[++top]=vex_ no ;
        p=p-> nextarc ;
         }
     }
  }while(boolean==0) ;
if (count<G->vexnum) return(-1) ;
else return(1);
}

算法分析:
设AOV网有n个顶点，e条边，则算法的主要执行是:
◆统计各顶点的入度: 时间复杂度是O(n+e) ;
◆入度为0的顶点入栈:时间复杂度是O(n) ;
◆排序过程:顶点入栈和出栈操作执行n次，入度减1的操作共执行e次，时间复杂度是O(n+e) ;因此，整个算法的时间复杂度是O(n+e)。

三.关键路径

算法思想
①利用拓扑排序求出AOE网的一个拓扑序列;
②从拓扑排序的序列的第一个顶点(源点)开始，按拓扑顺序依次计算每个事件的最早发生时间ve(i) ;
③从拓扑排序的序列的最后一个顶点(汇点)开始，按逆拓扑顺序依次计算每个事件的最晚发生时间vl(i) ;
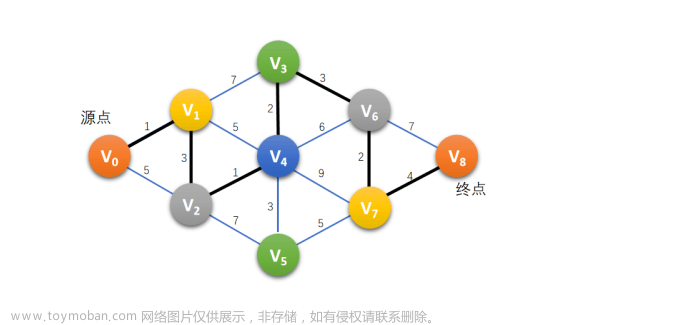
对于图7-24的AOE网，处理过程如下:拓扑排序的序列是:(Vo, V1, V2, V3,V4, V5, V6，V7，V8)
算法实现

void critical path(ALGraph *G)
{ int j,k,m; LinkNode *p ;
   if (Topologic_Sort(G)==-1)
       printf(“\nAOE网中存在回路，错误!!\n\n”) ;
   else
    { for( j=0; j<G->vexnum; j++)
           ve[j]=0 ;/*事件最早发生时间初始化*/
      for (m=0; m<G->vexnum; m++)
      { j=topol[m] ;
        p=G-> adjlist[j].firstarc ;
        for(; p!=NULL; p=p->nextarc )
        { k=p->adjvex ;
          if (ve[j]+p->weight>ve[k) 
              ve[k]=vel[jl+p->weight;
        }
      } /*计算每个事件的最早发生时间ve值*/
      for ( j=0; j<G->vexnum; j++) 
           vI[j]=ve[j] ; /* 事件最晚发生时间初始化*/
     for (m=G->vexnum-1; m>=0; m--)
          { j=topol[m] ; p=G->adjlistijJ.firstarc;
             for (; p!=NULL; p=p->nextarc )
              { k=p->adjvex ;
                if (vI[k]-p->weight<vI[j)
                  vI[i]=vl[k]-p->weight ;
              }
           } /*计算每个事件的最晚发生时间vI值*/
   for (m=0; m<G->vexnum; m++)
      { p=G->adjlist[m].firstarc ;
        for (; p!=NULL; p=p->nextarc )
          { k=p->adjvex ;
            if ( (ve[m]+p->weight=VI[k])
                 printf(“<%d, %d>, m,j"); 
          }
      }/*输出所有的关键活动*/
    }/* end ofelse */
   }