【动态规划】矩阵连乘问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了【动态规划】矩阵连乘问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 两个矩阵相乘：

【动态规划】矩阵连乘问题
代码如下：

void MatrixMutiply(int** a, int** b, int** c, int ra, int ca, int rb, int cb)
{
	if (ca != rb) return;
	for (int i = 0; i < ra; ++i)   //a的行
	{ 
		int sum = 0;
		for (int j = 0; i < cb; ++j)  //b的列
		{
			for (int k = 0; k < ca; ++k)  //a的列 
			{
				sum = a[i][k] * b[k][j];
			}
			c[i][j] = sum;
		}
	}
}

2. 三个矩阵相乘：

【动态规划】矩阵连乘问题
矩阵相乘，只有结合律没有交换律。
显而易见，三个矩阵相乘，有两种结合方式，（AB)C 比 A(BC)的值小的多。

3. 多个矩阵连乘，有多种结合方式

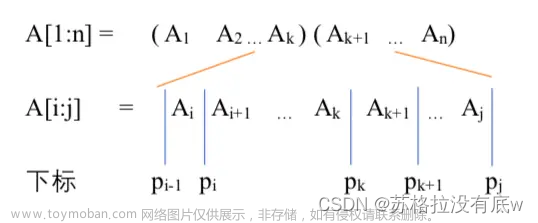
因此我们把它们进行划分，假设从第k个矩阵开始划分。如下图：就有
【动态规划】矩阵连乘问题
j个矩阵连乘的积 = R(第 i 个到第k矩阵的积 ) + U(第k+1到最后一个矩阵的积) + R*U 。

举个例子：

有6个矩阵如下图：
使 k = 2 ，则从第二个矩阵开始划分，得到如下：
【动态规划】矩阵连乘问题
使 k = 4 ，则从第二个矩阵开始划分，得到如下：

根据上面两幅图可以看出，红色绿色黄色，所对应得数组p下标所对应的值正好是R，U相乘需要的行和列。得示例可以得到如下关系：
【动态规划】矩阵连乘问题
代码如下：

int MaxtrixMut(int* dp, int i, int j)
{
	if (i == j) return 0;
	else
	{  
		//int t = MaxtrixMut(dp, i, i)+MaxtrixMut(dp,i+1,j)+dp[i-1]*dp[i]*dp[j];  
	    //k == i时
		int t = 0 + MaxtrixMut(dp,i+1,j)+dp[i-1]*dp[i]*dp[j];    
		//从i+1开始划分	
		for (int k = i+1; k < j; ++k)
			{
				int v = MaxtrixMut(dp,i,k)+MaxtrixMut(dp,k+1,j)+ dp[i - 1] * dp[k] * dp[j];	
			    if (t > v)
		   	    {
				  t = v;
		     	}
		     }
		return t;
	}
}

示例：

如果是从第一个到第四个矩阵的乘积，则可以划分为如下：其中红色均为重复划分。
【动态规划】矩阵连乘问题
去重以后的代码：

int MaxtrixMut_2(int* dp, int i, int j, vector<vector<int> >& vec)
{
	if (i == j) return 0;
	else if (vec[i][j] > 0)   //判断vec中是否有值
	{
		return vec[i][j];
	}
	else
	{    //k == i时
		 vec[i][j] = 0 + MaxtrixMut_2(dp, i + 1, j,vec) + dp[i - 1] * dp[i] * dp[j];
		//从i+1开始划分	
		for (int k = i + 1; k < j; ++k)
		{
			int v = MaxtrixMut_2(dp, i, k,vec) + MaxtrixMut_2(dp, k + 1, j,vec) + dp[i - 1] * dp[k] * dp[j];
			if (vec[i][j] > v)
			{
				vec[i][j] = v;
			}
		}
		return vec[i][j];
	}
}

运行结果：
【动态规划】矩阵连乘问题

int NiceMatrixChain_2(int p[], int n, vector<vector<int> >& m, vector<vector<int> >& s)
{
      ....................................
			m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j];
			s[i][j] = i;  //划分点
			for (int k = i + 1; k < j; ++k)
			{
				int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
				if (m[i][j] > t)
				{
					m[i][j] = t;
					s[i][j] = k;//   划分点
					..............................................
}

【动态规划】矩阵连乘问题

了解如何进行划分：代码如下：

按照
12 23 34 45 56
123 234 345 456
1234 2345 3456
12345 23456
123456 划分

void NiceMatrixChain(int p[],int n ,vector<vector<int> > &m)
{
	for (int i = 1; i <= n; ++i) m[i][i] = 0;  //让其对角线置为0  1，1  2，2  3，3  4，4  5，5  6，6
	for (int r = 2; r < n; ++r)   //循环的行数
	{
		for (int i = 1; i <= n - r + 1; ++i)   //循环的列数
		{
			int j = i + r - 1;
			for (int k = i; k <= j; ++k)
			{
				printf("%d", k);
			}
			printf(" ");
		}
		printf("\n");
	}

运行结果如下：
【动态规划】矩阵连乘问题
根据上面的代码，略加修改可以得到整个划分的过程。

【举个例子开始先是 12 23 34 45 56 进行相乘】
而123相乘可以分为 (12)3 1(23) 则只需要用上面已经得出的12 和 23 分别与矩阵三和矩阵1相乘，并比较处哪个较小。选较小的积。

int NiceMatrixChain_2(int p[], int n, vector<vector<int> >& m)
{
	for (int i = 1; i <= n; ++i) m[i][i] = 0;  //让其对角线置为0  1，1  2，2  3，3  4，4  5，5  6，6
	for (int r = 2; r <= n; ++r)   //循环的行数
	{
		for (int i = 1; i <= n - r + 1; ++i)   //循环的列数
		{
			int j = i + r - 1;
			m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j];
			for (int k = i+1; k < j; ++k)
			{
				int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
				if (m[i][j] > t)
				{
					m[i][j] = t;
				}
			}
			PrintVector(m);
		}
	}
	return	m[1][n];
}

测试代码如下；文章来源地址https://www.toymoban.com/news/detail-462287.html

int main()
{
	const int n = 6;
	int p[n+1] = { 30,35,15,5,10,20,25 };
//int sum = MaxtrixMut(p, 1, n);
	vector<vector<int> > vec(n+1, vector<int>(n + 1,0));//  int sum = MaxtrixMut_2(p, 1, n, vec);
// PrintVector(vec);
//	cout << sum << endl;
//	NiceMatrixChain(p, n, vec);
	int sum = NiceMatrixChain_2(p, n, vec);
	PrintVector(vec);
}