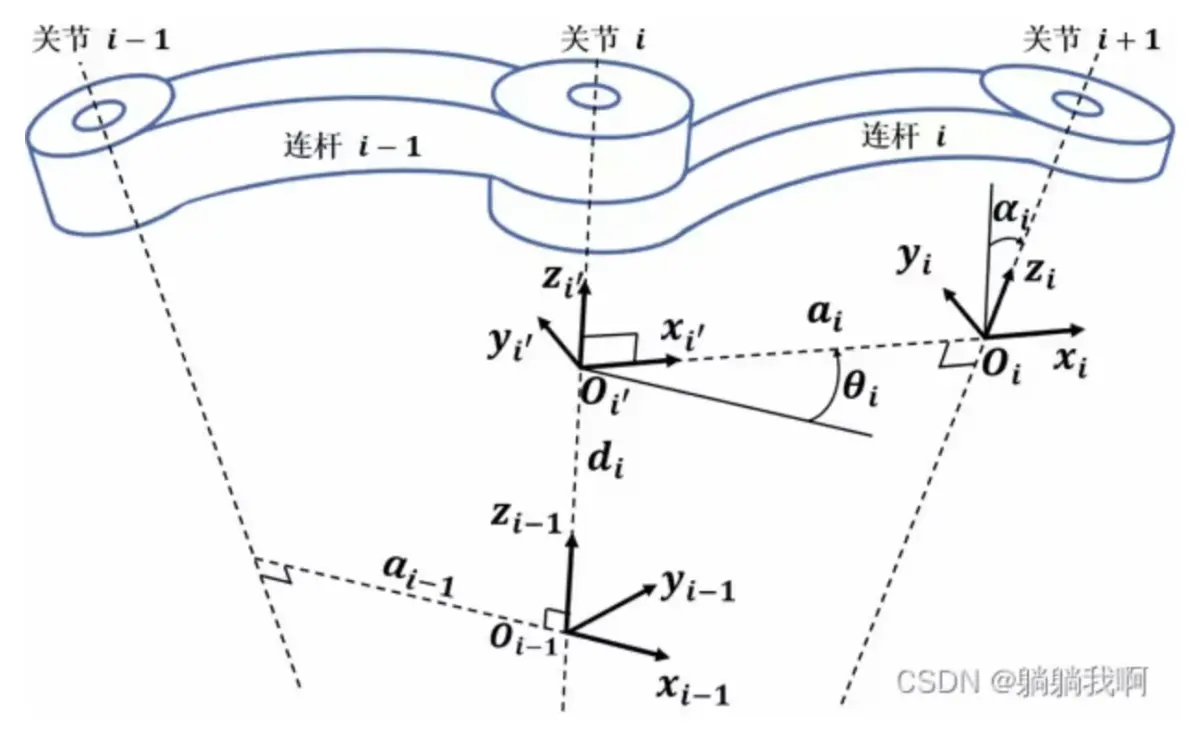
本文我们要做的是:给机器人一个末端坐标,使机器人自动调整姿态。为了使问题简单易懂,我们先以2自由度(XY平面中)的机器人为例,如下图为2自由度机器人的连杆机构模型。

其中P为末端点即手爪的位置,坐标为(x,y);L1、L2分别为两个手臂的长度,θ1、θ2分别为两个手臂的偏转角度。从几何学的观点来处理这个手爪位置(P)与偏转角度(θ1、θ2)的关系称为运动学(Kinematics)。
已知机器人的偏转角度(θ1、θ2),求其手爪位置P(x,y)的运动学问题称为正运动学(Direct Kinematics)。
给定手爪末端位置P(x,y),求出机器人的两个手臂的偏转角度(θ1、θ2)的运动学问题称为逆运动学(Inverse Kinematics)。
在之后的工程场景中,我们需要解决的问题是让机器人从传送带上抓取物体,物体的位置就是手爪最终位置P,因此,以下使用逆运动学方法更容易理解。
1. 二自由度机器人的逆运动学解法:
假设机械臂最初的姿态:与X轴重合
已知:x,y,L1,L2;求θ1、θ2
解:根据勾股定理得到:
所以得到
根据三角公式得到过渡角度θT: 得到:
得到:
根据余弦定理:
得到: 得到:
得到:
同理,θ2也使用余弦定理可得:

求出:
这样就得到了偏转角度θ1和θ2.
2.三自由度机器人的逆运动学解法:如果给机器人增加一个自由度,让它在三维空间中运动。那么我们可以看作将机器人整体偏转了一个角度θ3,在这个角度上建立一个辅助平面,这样就能看作机器人在这个辅助平面上的运动,又回到了二自由度的解算方法。所以,我们只要增加计算θ3角度,其他与二自由度解算方式相同。

假设机械臂最初的姿态:与X轴重合,已知:x,y,z,L1,L2;求θ1、θ2、θ3,解析如下图:

解:根据上图,可得  ,
,
那么  所以
所以  或者arctan(x,z)
或者arctan(x,z)
然后仿照二自由度机器人的方法,计算偏转平面上的θT、θ1和θ2:

 得到
得到 
 得到
得到 
求出
得到θT、θ1和θ2角度后,下面我们在Unity中使用脚本来实现。
本文中的方法,参照了grbl控制3轴机械臂 原理 实现 (二) 之3D机械臂模拟及实现_ourkix的博客文章来源:https://www.toymoban.com/news/detail-462457.html
加入自己的瞎琢磨,比较粗陋。且由于数学模型与实际模型的坐标差异,在实际程序中还需要有象限的变化,希望以后有空再改进。文章来源地址https://www.toymoban.com/news/detail-462457.html
到了这里,关于UnityVR--机械臂场景6-三自由度逆向解算1的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!