二叉树的顺序存储及基本操作-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树的顺序存储及基本操作。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

第1关：树和二叉树基本概念

1、在树中除根结点外，其余结点分成m(m≥0)个（A）的集合T1，T2，T3…Tm，每个集合又都是树，此时结点T称为Ti的父结点，Ti称为T的子结点（1≤i≤m）。

A、互不相交B、可以相交C、叶节点可以相交D、树枝结点可以相交
2、在一棵度为3的树中，度为3的结点数为2个，度为2的结点数为1个，度为1 的结点2个，则度为0的结点数为（C）个。

A、4B、5C、6D、7
3、如果结点A有三个兄弟，而且B是A的双亲，则B的出度是（B）。

A、3B、4C、5D、1
4、已知一棵完全二叉树的结点总数为9个，则最后一层的结点数为（B）。

A、1B、2C、3D、4
5、假设在一个二叉树中，双分支结点数为15，单分支结点数为32，则叶子结点数为（B）个。

A、15B、16C、17D、18
6、在完全二叉树中，当i为奇数且不等于1时，结点i的左兄弟是结点（D），否则没有左兄弟。

A、2i-1B、i+1C、2i+1D、i-1
7、在一棵二叉树上第4层的结点数最多为（D）。

A、2B、4C、6D、8
8、假定一棵三叉树的结点数为50，则它的最小高度为（C）。

A、3B、4C、5D、6
9、一个深度为L的满K叉树有如下性质：第L层上的结点都是叶子结点，其余各层上每个结点都有K棵非空子树。如果按层次顺序从1开始对全部结点编号，编号为n的有右兄弟的条件是（B）。

A、(n-1)%k0B、(n-1)%k!=0C、n%k0D、n%k!=0

第2关：二叉树的顺序存储及基本操作

任务描述

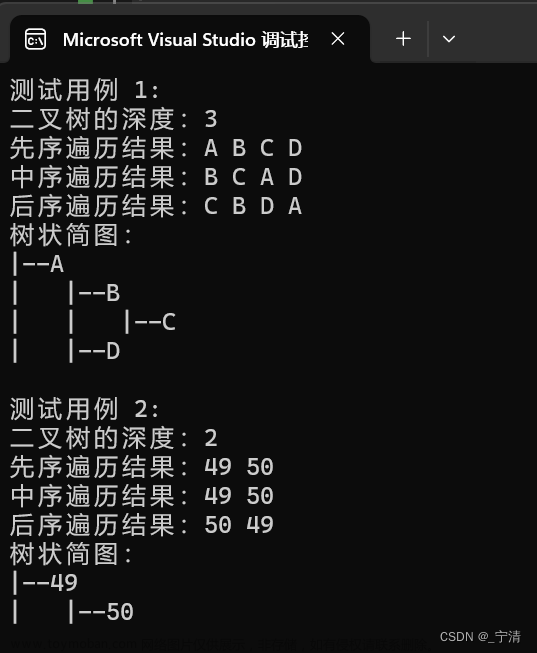
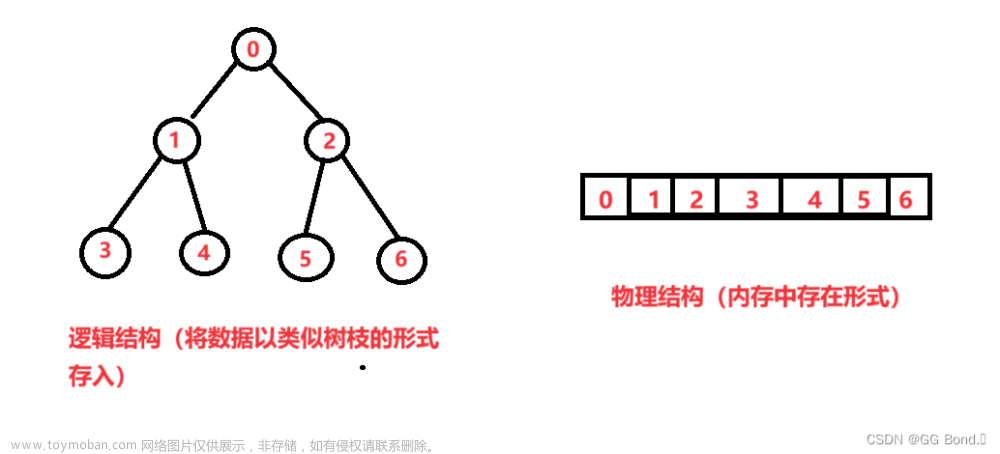
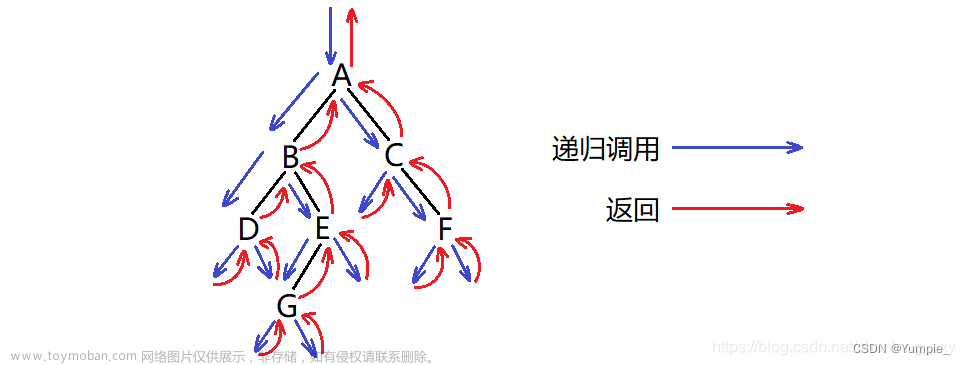
本关任务：以顺序结构存储二叉树，编写前序、中序、后序及层次顺序遍历二叉树的算法，并计算二叉树深度、所有结点总数。

测试说明

平台会对你编写的代码进行测试：

测试输入：ABCDEF###G##H

预期输出：
按先序遍历的结果为:ABDEGCFH
按中序遍历的结果为:DBGEAFHC
按后序遍历的结果为:DGEBHFCA
按层序遍历的遍历结果为:ABCDEFGH
该二叉树的高度为:4文章来源地址https://www.toymoban.com/news/detail-462561.html

代码如下

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
using namespace std;

#define OK  1
#define ERROR 0

#define MAX_TREE_SIZE  100

typedef  char TElemType ;

typedef  TElemType  SqBiTree[MAX_TREE_SIZE];

TElemType Nil='#';

void input(TElemType &x)	 // 函数变量
{
	scanf("%c",&x);
}

void visit(TElemType x)	 // 函数变量
{
	printf("%c",x);
}

void InitBiTree(SqBiTree &T)
{ // 构造空二叉树T。因为T是数组名，故不需要&
	int i;
	for(i=0;i<MAX_TREE_SIZE;i++)
		T[i]=Nil; // 初值为空(Nil在主程中定义)
}


void CreateBiTree(SqBiTree &T)
{ // 按层序次序输入二叉树中结点的值(字符型或整型), 构造顺序存储的二叉树T
	/********** Begin **********/ 
	int i=1;
	scanf("%s",T+1);
	while(T[i] != '\0')
		i++;
	T[i]='#';
	/********** End **********/
}

int BiTreeEmpty(SqBiTree T)
{ // 初始条件：二叉树T存在。操作结果：若T为空二叉树，则返回TRUE，否则FALSE
	if(T[1]==Nil) // 根结点为空，则树空
		return 1;
	else
		return 0;
}

int BiTreeDepth(SqBiTree T)
{ // 初始条件：二叉树T存在。操作结果：返回T的深度
	/********** Begin **********/ 
	int i=MAX_TREE_SIZE-1,j;
	while(T[i]=='#')
		i--;
	j=i;
	int dep=0;
	do{
		dep++;
		j=j/2;
	}while(j>=1);
	return dep;
	
	/********** End **********/
}
void PreTraverse(SqBiTree T,int e)
{ // PreOrderTraverse()调用
	/********** Begin **********/ 
	if(T[e] != '#'){
		visit(T[e]);
		PreTraverse(T,2*e);
		PreTraverse(T,2*e+1);
	}
	/********** End **********/
}
void PreOrderTraverse(SqBiTree T,void(*Visit)(TElemType))
{ // 初始条件：二叉树存在，Visit是对结点操作的应用函数
	// 操作结果：先序遍历T，对每个结点调用函数Visit一次且仅一次
	if(!BiTreeEmpty(T)) // 树不空
		PreTraverse(T,1);
	printf("\n");
}

void InTraverse(SqBiTree T,int e)
{ // InOrderTraverse()调用
	/********** Begin **********/ 
	if(T[e] != '#'){
		InTraverse(T,2*e);
		visit(T[e]);
		InTraverse(T,2*e+1);
	}   
	/********** End **********/
}

void InOrderTraverse(SqBiTree T,void(*Visit)(TElemType))
{ // 初始条件：二叉树存在，Visit是对结点操作的应用函数
	// 操作结果：中序遍历T，对每个结点调用函数Visit一次且仅一次
	if(!BiTreeEmpty(T)) // 树不空
		InTraverse(T,1);
	printf("\n");
}

void PostTraverse(SqBiTree T,int e)
{ // PostOrderTraverse()调用
	/********** Begin **********/ 
	if(T[e] != '#'){
		PostTraverse(T,2*e);
		PostTraverse(T,2*e+1);
		visit(T[e]);
	}
	/********** End **********/
}

void PostOrderTraverse(SqBiTree T,void(*Visit)(TElemType))
{ // 初始条件：二叉树T存在，Visit是对结点操作的应用函数
	// 操作结果：后序遍历T，对每个结点调用函数Visit一次且仅一次
	if(!BiTreeEmpty(T)) // 树不空
		PostTraverse(T,1);
	printf("\n");
}

void LevelOrderTraverse(SqBiTree T,void(*Visit)(TElemType))
{ // 层序遍历二叉树
	/********** Begin **********/ 
	int dep=BiTreeDepth(T);
	int tree_max=pow(dep,2)-1;
	for(int i=1;i<tree_max;i++){
		if(T[i]=='#')
			continue;
		visit(T[i]);
	}
	/********** End **********/
}

int main()
{
	TElemType e;
	SqBiTree Bt;
	InitBiTree(Bt);
	CreateBiTree(Bt);    
	printf("按先序遍历的结果为:");
	PreOrderTraverse(Bt,visit);
	printf("按中序遍历的结果为:");
	InOrderTraverse(Bt,visit);
	printf("按后序遍历的结果为:");
	PostOrderTraverse(Bt,visit);
	printf("按层序遍历的遍历结果为:");
	LevelOrderTraverse(Bt,visit);  
	printf("\n该二叉树的高度为:%d",BiTreeDepth(Bt) );
	return 0;
}