torch中的矩阵乘法与广播机制-Toy模板网

这篇具有很好参考价值的文章主要介绍了torch中的矩阵乘法与广播机制。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

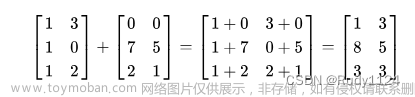
一. 广播机制 broadcast

1. 两个张量“可广播”规则：

每个张量至少有一个维度。
当迭代维度大小时，从最后一个维度开始，满足以下条件：（1）维度大小相等，（2）其中一个维度为1，（3）或者其中一个维度不存在。

举例：

x=torch.empty((0,))
y=torch.empty(2,2)
# x，y不可广播，因为x至少没有一个维度


x=torch.empty(5,7,3)
y=torch.empty(5,7,3)
# 相同的形状总是可广播的


x=torch.empty(5,3,4,1)
y=torch.empty(  3,1,1)
# 第一个尾维度:大小都为1
# 第二个尾维度:y的大小为1
# 第三个尾维度:x的大小== y的大小
# 第四个尾维度，y维不存在
# 满足可广播规则，因此X和y是可广播的。

x=torch.empty(5,2,4,1)
y=torch.empty(  3,1,1)
# x和y是不可广播的，因为在第三个尾维度中2 != 3

2. 可广播张量计算规则：

如果两个张量可以广播，则得到的张量大小计算如下:

如果x和y的维数不相等，在维数较少的张量的维数前加上1，使它们长度相等。
对于每个维度大小，生成的维度大小是该维度上x和y大小的最大值。

举例：

>>> x=torch.empty(5,1,4,1)
>>> y=torch.empty(  3,1,1)
>>> (x+y).size()
torch.Size([5, 3, 4, 1])


>>> x=torch.empty(1)
>>> y=torch.empty(3,1,7)
>>> (x+y).size()
torch.Size([3, 1, 7])

>>> x=torch.empty(5,2,4,1)
>>> y=torch.empty(3,1,1)
>>> (x+y).size()
RuntimeError: The size of tensor a (2) must match the size of tensor b (3) at non-singleton dimension 1

注意1：原地操作不允许原地张量因广播而改变形状。

>>> x=torch.empty(5,3,4,1)
>>> y=torch.empty(3,1,1)
>>> (x.add_(y)).size()
torch.Size([5, 3, 4, 1])

# but:
>>> x=torch.empty(1,3,1)
>>> y=torch.empty(3,1,7)
>>> (x.add_(y)).size() # in_place
RuntimeError: The expanded size of the tensor (1) must match the existing size (7) at non-singleton dimension 2.

>>> (x+y).size()
torch.Size([3,3,7])

注意2：在两个张量没有相同形状，但可广播且具有相同数量的元素的情况下，广播的引入可能导致向后不兼容的变化。

以前会产生一个大小为torch.Size([4,1])的张量，但现在产生一个大小为torch.Size([4,4])的张量。为了帮助识别代码中可能存在广播引入的向后不兼容的情况，可以设置torch.utils.backcompat_broadcast_warning。enabled为True，在这种情况下将生成python警告。

>>> torch.utils.backcompat.broadcast_warning.enabled=True
>>> torch.add(torch.ones(4,1), torch.ones(4))
__main__:1: UserWarning: self and other do not have the same shape, but are broadcastable, and have the same number of elements.
Changing behavior in a backwards incompatible manner to broadcasting rather than viewing as 1-dimensional.

二. torch的各种乘法操作

1. torch.dot(vec1,vec2)

用来计算两个向量的点积，不支持broadcast操作，要求两个一维张量的元素个数相同。

import torch

vec1 = torch.Tensor([1,2,3,4])
vec2 = torch.Tensor([5,6,7,8])
print(torch.dot(vec1, vec2))
# tensor(70.)

2. torch.mm(mat1,mat2)

用来计算两个二维矩阵的矩阵乘法，不支持broadcast操作，要求两个Tensor的维度满足矩阵乘法的要求。

mat1 = torch.randn(3, 4)
mat2 = torch.randn(4, 5)
out = torch.mm(mat1, mat2)
print(out.shape)
# torch.Size([3, 5])

3. torch.bmm(mat1,mat2)

用来计算两个三维带Batch矩阵乘法，不支持broadcast操作，要求该函数的两个输入必须是三维矩阵且第一维相同（表示Batch维度）。

mat1 = torch.randn(2, 3, 4)
mat2 = torch.randn(2, 4, 5)
out = torch.bmm(mat1, mat2)
print(out.shape)
# torch.Size([2, 3, 5])

4. torch.mv(mat,vec)

用于计算矩阵和向量之间的乘法（矩阵在前，向量在后），不支持broadcast操作，要求矩阵与向量满足矩阵乘法的要求。

mat = torch.randn(3, 4)
vec = torch.randn(4)
output = torch.mv(mat, vec)
print(output.shape)
# torch.Size([3])

5. torch.mul(a,b)

troch.multiply()等同于torch.mul()；

用于计算矩阵逐元素(Element-wise)乘法（点乘），支持broadcast操作，只要a,b的维度满足broadcast条件，就可以进行逐元素乘法操作。

A = torch.randn(2,1,4)
B = torch.randn(3, 1) # 矩阵
print(torch.mul(A,B).shape)
# torch.Size([2, 3, 4])
b0 = 2 # 标量
print(torch.mul(A,b0).shape)
# torch.Size([2, 1, 4])
b1 = torch.tensor([1,2,3,4]) # 行向量
print(torch.mul(A,b1).shape)
# torch.Size([2, 1, 4])
b2 = torch.Tensor([1,2,3]).reshape(-1,1) # 列向量
print(torch.mul(A,b2).shape)
# torch.Size([2, 3, 4])

6. torch.matmul(mat1,mat2)

几乎可用于计算所有矩阵/向量相乘的情况，支持broadcast操作，可以理解为torch.mm的broadcast版本，其乘法规则视参与乘法的两个张量的维度而定。

特别的，针对多维数据 matmul()乘法，可以认为该 matmul()乘法使用两个参数的后两个维度来计算，其他的维度都可以认为是batch维度。

mat1 = torch.randn(2,1,4,5)
mat2 = torch.randn(2,1,5,2)
out = torch.matmul(mat1, mat2)
print(out.shape)
# torch.Size([2, 1, 4, 2])

若两个矩阵是一维的，那么该函数的功能与torch.dot()一样，返回两个一维tensor的点乘结果；

vec1 = torch.Tensor([1,2,3,4])
vec2 = torch.Tensor([5,6,7,8])
print(torch.matmul(vec1, vec2))
# tensor(70.)
print(torch.dot(vec1, vec2))
# tensor(70.)

若两个矩阵是二维的，那么该函数的功能与torch.mm()一样，返回两个二维矩阵的矩阵乘法；

mat1 = torch.randn(3, 4)
mat2 = torch.randn(4, 5)
out = torch.mm(mat1, mat2)
print(out.shape)
# torch.Size([3, 5])

out1 = torch.matmul(mat1, mat2)
print(out1.shape)
# torch.Size([3, 5])

若第一个参数是二维张量（矩阵），第二个参数是一维张量（向量），那么将返回矩阵×向量的积。那么该函数的功能与torch.mv()一样，要求矩阵和向量满足矩阵乘法的要求；

mat = torch.randn(3, 4)
vec = torch.randn(4)
output = torch.mv(mat, vec)
print(output.shape)
# torch.Size([3])

output1 = torch.matmul(mat, vec)
print(output1.shape)
# torch.Size([3])

若第一个参数是一维张量，第二个参数是二维张量，那么在一维张量的前面增加一个维度（broadcast），然后进行矩阵乘法；

vec = torch.randn(4)
mat = torch.randn(4,2)
print(torch.matmul(vec, mat).shape)
# torch.Size([2])

7. 运算符

@ 运算符 : 其作用类似于torch.matmul。

mat1 = torch.randn(2,1,4,5)
mat2 = torch.randn(2,1,5,2)
out = torch.matmul(mat1, mat2)
print(out.shape)
# torch.Size([2, 1, 4, 2])
out1 = mat1 @ mat2
print(out1.shape)
# torch.Size([2, 1, 4, 2])

* 运算符 : 其作用类似于torch.mul。

A = torch.randn(2,1,4)
B = torch.randn(3, 1) # 矩阵
print(torch.mul(A,B).shape)
# torch.Size([2, 3, 4])

print((A * B).shape)
# torch.Size([2, 3, 4])

8.扩展：torch.einsum()：爱因斯坦求和约定

放个链接： einsum is all you need!

如果你像我一样，发现记住PyTorch/TensorFlow中那些计算点积、外积、转置、矩阵-向量乘法、矩阵-矩阵乘法的函数名字和签名很费劲，那么einsum记法就是我们的救星。einsum记法是一个表达以上这些运算，包括复杂张量运算在内的优雅方式，基本上，可以把einsum看成一种领域特定语言。一旦你理解并能利用einsum，除了不用记忆和频繁查找特定库函数这个好处以外，你还能够更迅速地编写更加紧凑、高效的代码。而不使用einsum的时候，容易出现引入不必要的张量变形或转置运算，以及可以省略的中间张量的现象。

仅为学习记录！文章来源地址https://www.toymoban.com/news/detail-463247.html

到了这里，关于torch中的矩阵乘法与广播机制的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！