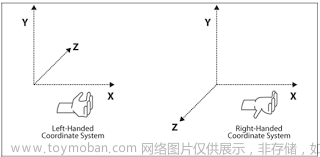
前文输出了cesium的Rotation变量,一个矩阵;把这矩阵写下来看下;
0.99939 -0.034899 0 0
0.034899 0.99939 0 0
0 0 1 0
0 0 0 1
看一下3D数学的相关描述;
方位和角位移
不能用绝对坐标来描述物体的 位置 ,要描述物体的 位置 ,必须把物体放置于特定的参考系中。
描述 位置 实际上就是描述相对于给定参考点(通常是坐标系的原点)的 位移 。
描述物体 方位 时,也不能使用绝对量。
与位置只是相对已知点的位移一样,方位是通过于相对已知方位(通常称为“单位”方位或“源”方位)的旋转来描述的。
旋转的量称作角位移。
在数学上描述 方位 就等价与描述 角位移 。
方位:
表示的是一种静态的状态;
当用矩阵表示方位时,此时矩阵表示的是一个“点”,而该点的坐标就是原点进行矩阵表示的旋转之后所在的地方。即描述 方位 实际上就是描述相对于给定参考点(通常是坐标系的原点)的 角位移 。
角位移:
表示的是一种动态的过程;
当用矩阵表示角位移时,旋转变换的量即是角位移。
具体来说,我们用矩阵和四元数来表示“角位移”,用欧拉角来表示“方位”。
矩阵形式--用矩阵描述旋转变换
3D 中,描述坐标系中 方位 的一种方法就是列出这个坐标系的 基向量 ,而这些基向量是相对于其他坐标系进行描述的。
这些基向量构成一个 3 × 3 矩阵,然后就能用矩阵形式来描述 方位 。
换言之,能用一个 旋转矩阵 来描述这两个坐标系之间的相对方位,这个旋转矩阵用于把一个坐标系中的向量转换到另一个坐标系中。
看了一下,如下图;有三种情况的旋转矩阵,分别是绕不同的轴旋转,其需要的矩阵不一样;

上面的矩阵应该是绕Z轴旋转;只是多了最后一行最后一列;如果去除最后一行一列就是如下;
0.99939 -0.034899 0
0.034899 0.99939 0
0 0 1
这就和前面绕Z轴旋转的矩阵一样;文章来源:https://www.toymoban.com/news/detail-463279.html
因为最后一行一列是 0 0 0 1;乘上去是不是一样;文章来源地址https://www.toymoban.com/news/detail-463279.html
到了这里,关于认识3D旋转变换矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!