数据结构：二叉树的基本操作（用递归实现）-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构：二叉树的基本操作（用递归实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

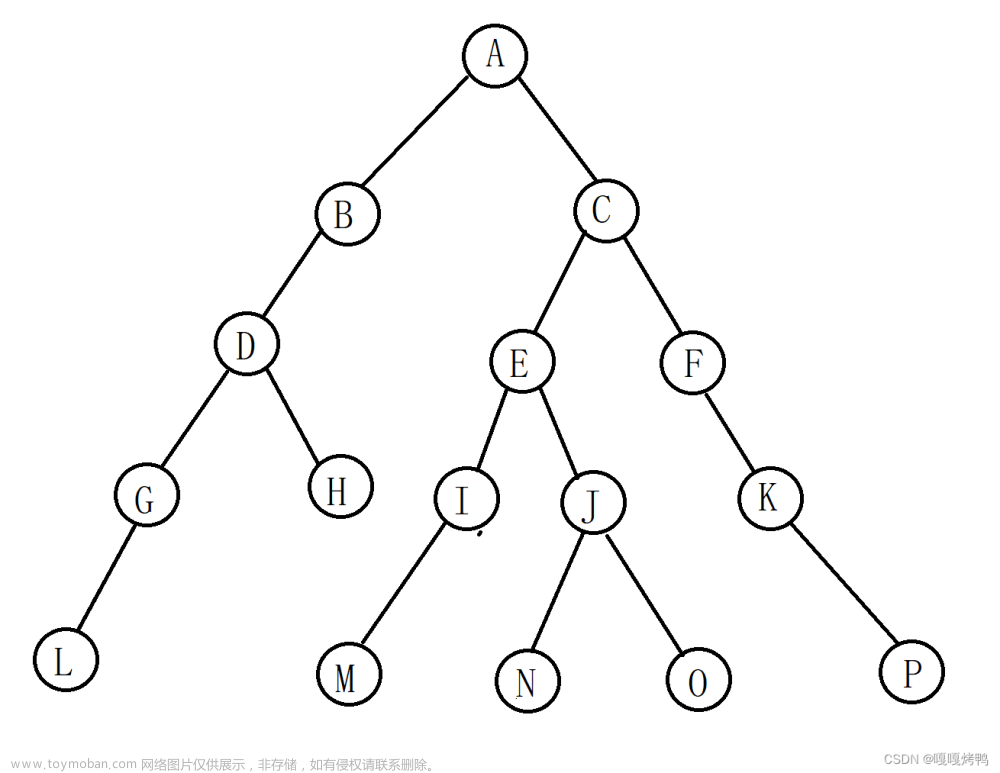
本文将通过完成以下内容来展示二叉树的基本操作，代码解释标注全面而且清晰，代码书写也十分规范，适合初学者进行学习，本篇文章算是本人的一些学习记录分享，希望对有需要的小伙伴提供一些帮助~

本文的内容为：

用递归的方法实现以下算法：

1．以二叉链表表示二叉树，建立一棵二叉树（算法5.3）；

2．输出二叉树的中序遍历结果（算法5.1）；

3．输出二叉树的前序遍历结果（见讲稿）；

4．输出二叉树的后序遍历结果（见讲稿）；

5．计算二叉树的深度（算法5.5）；

6．统计二叉树的结点个数（算法5.6）；

7．统计二叉树的叶结点个数；

8．统计二叉树的度为1的结点个数；

代码如下所示：

1、源程序及主要算法说明
#include<iostream>
using namespace std;

//二叉树的二叉链表存储表示
typedef struct BiNode
{				
	char data;						//结点数据域
	struct BiNode *lchild,*rchild;	//左右孩子指针
}BiTNode,*BiTree;

//1. 以二叉链表表示二叉树，建立一棵二叉树（算法5.3）；
void CreateBiTree(BiTree &T)
{	
//按先序次序输入二叉树中结点的值（一个字符），创建二叉链表表示的二叉树T
	char ch;
	cin>>ch;
	if(ch=='#')   T=NULL;  	//递归结束，建空树
	else{
   	 	T=new BiTNode;    T->data=ch; 	//生成根结点
		cout<<"请输入"<<T->data<<"的左孩子(没有左孩子输入#)";
    	CreateBiTree(T->lchild);  //递归创建左子树
   		cout<<"请输入"<<T->data<<"的右孩子(没有左孩子输入#)";
    	CreateBiTree(T->rchild); //递归创建右子树
  }																	
}									//CreateBiTree
//2．输出二叉树的中序遍历结果（算法5.1）；					
void InOrderTraverse(BiTree T)
{  
 	if(T){   
     InOrderTraverse(T->lchild); 
     cout<<T->data;
     InOrderTraverse(T->rchild);}
}

//3．输出二叉树的前序遍历结果（见讲稿）；
void PreOrderTraverse(BiTree T)
{
	if(T){     
     cout<<T->data; 
     PreOrderTraverse(T->lchild); 
     PreOrderTraverse(T->rchild);
} 
}
// 4．输出二叉树的后序遍历结果（见讲稿）；
void PostOrderTraverse(BiTree T)
{
	if(T){
     PostOrderTraverse(T->lchild); 
     PostOrderTraverse(T->rchild); 
     cout<<T->data; 
} 
}

//5．计算二叉树的深度（算法5.5）；
int Depth(BiTree T) {
{    int m,n;
	if(T == NULL ) return 0;        //如果是空树，深度为0，递归结束
	else 
	{	m=Depth(T->lchild);			//递归计算左子树的深度记为m
		n=Depth(T->rchild);			//递归计算右子树的深度记为n
		if(m>n) return(m+1);		//二叉树的深度为m 与n的较大者加1
		else return (n+1);
	}
}
}

//6．统计二叉树的结点个数（算法5.6）；
int NodeCount(BiTree T){
 	if(T==NULL) return 0;  			// 如果是空树，则结点个数为0，递归结束
     	else return NodeCount(T->lchild)+ NodeCount(T->rchild) +1;
    	 //否则结点个数为左子树的结点个数+右子树的结点个数+1
} 

//7．统计二叉树的叶结点个数；
int LeafCount(BiTree T){
 	if(T==NULL) 	//如果是空树返回0
		return 0;
	if (T->lchild == NULL && T->rchild == NULL)
		return 1; //如果是叶子结点返回1
	else return LeafCount(T->lchild) + LeafCount(T->rchild);
}

//8．统计二叉树的度为1的结点个数；
//	n=n0+n1+n2; n2=n0-1; n1=n-n0-n2=n-n0-(n0-1)=n-2n0+1
int n1Count(BiTree T,int n,int n0){
	if(T==NULL) 	//如果是空树返回0
		return 0;
	
	int n1=0; 
	n1=n-2*n0+1;
	
	if (n1<0) 
		return 0;
		
	return n1;
}

int main()
{
	BiTree tree;
	cout<<"请输入建立二叉链表的序列：\n";
	cout<<"请输入根节点：";
	CreateBiTree(tree);
	
	cout<<"所建立的二叉链表先序序列：\n";
	PreOrderTraverse(tree);
	cout<<"\n";
	cout<<"所建立的二叉链表中序序列：\n";
	InOrderTraverse(tree);
	cout<<"\n";
	cout<<"所建立的二叉链表后序序列：\n";
	PostOrderTraverse(tree);
	cout<<"\n";
	
	int depth = Depth(tree);
	cout<<"所建立的二叉链表深度是：\n";
	cout << "depth = " << depth;
	cout<<"\n";
	
	cout<<"所建立的二叉链表结点个数是：\n";
	int nodeCount = NodeCount(tree);
	cout << "nodeCount(n) = " << nodeCount;
	cout<<"\n";
	
	cout<<"所建立的二叉链表叶结点个数是：\n";
	int leafCount = LeafCount(tree);
	cout << "leafCount(n0) = " << leafCount;
	cout<<"\n";
	
	cout<<"所建立的二叉链表度为1的结点个数是：\n";
	int n1 = n1Count(tree,nodeCount,leafCount);
	cout << "n1 = " <<n1 ;
	cout<<"\n";
	
	cout<<endl;
	return 0;
}

运行结果如下：

数据结构：二叉树的基本操作（用递归实现）