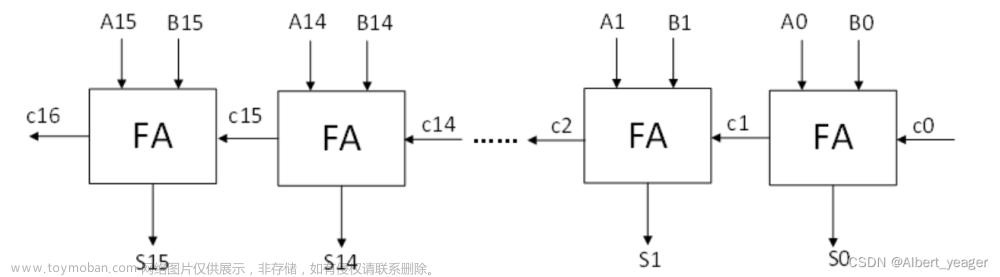
verilog实现除法器运算-Toy模板网

这篇具有很好参考价值的文章主要介绍了verilog实现除法器运算。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

verilog实现除法器运算

本文通过verilog实现了一个位宽参数可配置的除法运算模块

1，设计思路

我们要计算 a_data/b_data = div_data ----remain_data;

🌿 确定位宽：若a_data的位宽为A_WIDTH， b_data的位宽为B_WIDTH；则div_data的最大位宽为A_WIDTH, remain_data的位宽为B_WIDTH;
🍃 计算div_data的最高位：若a_data >= (b_data<<(A_WIDTH-1)), 则div_data的最高位div_data[A_WIDTH-1]为1，否则div_data[A_WIDTH-1]为0；即div_data[A_WIDTH-1] = a_data > (b_data<<(A_WIDTH-1)) ？ 1‘b1 : 1’b0;
🌾 计算div_data的次高位：若div_data的最高位div_data[A_WIDTH-1]为1，则a_data_tmp = a_data – (b_data<<(A_WIDTH-1)); 否则a_data_tmp = a_data; 次高位div_data[A_WIDTH-2] = a_data_tmp >= (b_data<<(A_WIDTH-2)) ？ 1‘b1 : 1’b0;
🌴 依次类推，可 计算出完整的div_data;
🌲. 计算完div_data后，可用 remain_data = a_data – b_data*div_data获取余数；

举个例子，计算8/3 也就是 4’b1000/3’b011 = 3’b010;

🥝 div_data[3] = 4’b1000 > (3’b011 << 3) ? 1’b1 : 1’b0 ; 由于div_data[3]为0，所以a_data_tmp为4‘b1000;
🥑 div_data[2] = 4’b1000 > (3’b011 << 2) ? 1’b1 : 1’b0; 由于div_data[2]为0，所以a_data_tmp为4‘b1000;
🍇 div_data[1] = 4’b1000 > (3’b011 << 1) ? 1’b1 : 1’b0; 由于div_data[1]为1，所以a_data_tmp为4‘b1000-(3’b011 << 1) = 4’b0010;
🍒 div_data[0] = 4’b0010 > (3’b011 << 0) ? 1’b1 : 1’b0;
🍐所以 div_data = 4‘b0010 = 2;
🌼 remain_data = a_data – b_data*div_data = 8 – 3 * 2 = 2 = 3’b010;

2， Verilog代码

// Filename      : div.v
// Author        : ppkuan
module div(/*autoarg*/
    //Inputs
    clk, rst_n, in_vld, a_data, b_data, 

    //Outputs
    out_vld, remain_data, div_data
);

parameter   A_WIDTH = 10;
parameter   B_WIDTH = 5;
// a_data/b_data = div_data------remain_data

input                             clk         ;
input                             rst_n       ;
input                             in_vld      ;
input       [A_WIDTH - 1 : 0]     a_data      ;
input       [B_WIDTH - 1 : 0]     b_data      ;

output reg                        out_vld     ;
output reg  [B_WIDTH - 1 : 0]     remain_data ;
output reg  [A_WIDTH - 1 : 0]     div_data    ;


wire   [A_WIDTH - 1 : 0]                             div_data_tmp    ;
wire   [A_WIDTH - 1 : 0] [A_WIDTH + B_WIDTH - 1 : 0] ab_data_tmp     ;
wire   [A_WIDTH - 1 : 0] [A_WIDTH - 1 : 0]           a_data_tmp      ; 
wire   [B_WIDTH - 1 : 0]                             remain_data_tmp ;

assign  ab_data_tmp[A_WIDTH - 1]   = b_data << (A_WIDTH - 1);
assign  div_data_tmp[A_WIDTH - 1]  = {{B_WIDTH{1'b0}}, a_data} >= ab_data_tmp[A_WIDTH - 1] ? 1'b1 : 1'b0;
assign  a_data_tmp[A_WIDTH - 1]    = div_data_tmp[A_WIDTH - 1] ? {{B_WIDTH{1'b0}},a_data} - ab_data_tmp[A_WIDTH - 1] : a_data;

genvar i;
generate 
    for(i = A_WIDTH - 2; i >= 0; i--)
        begin:div
            assign ab_data_tmp[i]  = (b_data << i);
            assign div_data_tmp[i] = {{B_WIDTH{1'b0}}, a_data_tmp[i+1]} >= ab_data_tmp[i] ? 1'b1 : 1'b0;
            assign a_data_tmp[i]   = div_data_tmp[i] ? {{B_WIDTH{1'b0}},a_data_tmp[i+1]} - ab_data_tmp[i] : a_data_tmp[i + 1];
        end
endgenerate

assign remain_data_tmp = {{B_WIDTH{1'b0}}, a_data} - div_data_tmp * b_data;

always@(posedge clk or negedge rst_n)
    if(!rst_n)
    begin
        out_vld     <= 'b0            ;
        remain_data <= 'd0            ;
        div_data    <= 'd0            ;
    end
    else if(in_vld)
    begin
        out_vld     <= 'b1            ;
        remain_data <= remain_data_tmp;
        div_data    <= div_data_tmp   ;
    end
    else 
    begin
        out_vld     <= 'b0            ;
    end
endmodule

3，测试用例：

module test;

wire         clk         ;
wire         rst_n       ;
wire         in_vld      ;
wire [9 : 0] a_data      ;
wire [4 : 0] b_data      ;
wire         out_vld     ;
wire [9 : 0] div_data    ;
wire [4 : 0] remain_data ;

reg         clk_r       ;
reg         rst_n_r     ;
reg         in_vld_r    ;
reg [9 : 0] a_data_r    ;
reg [4 : 0] b_data_r    ;
 
assign clk    = clk_r    ;
assign rst_n  = rst_n_r  ;
assign in_vld = in_vld_r ;
assign a_data = a_data_r ;
assign b_data = b_data_r ;

div#(
    .A_WIDTH(10),
    .B_WIDTH(5)) 
    u_div(/*autoinst*/
    // a_data/b_data = div_data------remain_data

    .clk                            (clk                                        ), // input 
    .rst_n                          (rst_n                                      ), // input 
    .in_vld                         (in_vld                                     ), // input 
    .a_data                         (a_data[9 : 0]                              ), // input 
    .b_data                         (b_data[4 : 0]                              ), // input 

    .out_vld                        (out_vld                                    ), // output
    .remain_data                    (remain_data[4 : 0]                         ), // output
    .div_data                       (div_data[9 : 0]                            )  // output
);

initial
begin
clk_r =    0;
in_vld_r = 0;
rst_n_r =  1;
#10
rst_n_r =  0;
#10
rst_n_r =  1;
#10
in_vld_r = 1;
a_data_r = 10'd57;
b_data_r = 5'd8;
#10
in_vld_r = 0;
$finish;
end

always #5 clk_r = !clk_r;

endmodule