CNN卷积神经网络
一、 什么是CNN卷积神经网络
卷积神经网络由三部分组成:输入层、由n个卷积层和池化层的组合组成、全连结的多层感知机分类器。
深度学习的迅速发展,我们会在不同的应用场景会使用不同的神经网络,没有一个神经网络他能在任何场景下,效果都好,也没有说某一个算法,在任何场景上都比其他算法要好,都是根据应用场景、最终的任务、数据集等来选择对应的神经网络,如CNN卷积神经网络,他在处理图像图片领域中,有着非常好的效果。
那为什么要用卷积神经网络而不直接用通用的神经网络呢?
(1) 现在一张图像像素非常大,如果将图像展开成向量输入,那么输入数据会非常大,从而参数过多导致效率低下,训练困难
(2) 将图像展开会丢失图片的空间信息
(3) 大量的参数会导致网络容易过拟合
二、 卷积
卷积是一种积分变换的数学方法。
输入一副图像,我们能经过特定设计的卷积核进行卷积操作后,输出的图像将会得到模糊、边缘强化等效果。即图像通过卷积核进行操作卷积,不同的卷积核能获取到图像的不同特征。
图像的卷积过程是怎么样的呢?
首先,输入维度是4×4,输入中红色部分,先和核函数中的元素对应相乘,就是输出中左上角的元素值s1,即 s1 = a×k1+b×k2+e×k3+f×k4。
当我们要对整个图像进行卷积,那么卷积核就要在整个图像上进行移动,从而对输入的图像像素都做一次卷积操作。
当我们要进行卷积之前,要选择好卷积核的大小,步长,是否对图像进行padding(填充),然后在进行卷积。
卷积核大小:
卷积核的大小一般为奇数,常用的有3x3,5x5,7x7,卷积核内的值,除了是已经设计好的卷积核,如Seber算子等等,其余大部分都是通过神经网络反向传播去学习更新的。
卷积核的步长:
是指对图像进行一次卷积后,下一次卷积时,卷积核应该平移多少个像素点的距离后,再进行卷积。图像在不进行填充的情况下做卷积,最终输出的图像会小于输入的图像。
图像的padding(填充):
为了图像卷积后输出的图像大小不发生变化、保留我们的边框信息,所以要对原始图像进行填充
填充的尺寸大小,与我们的卷积核大小相关。
一般填充有以下四种常用的,零填充,最近邻填充、循环填充
输入图像如下:
零填充:
最近邻填充:
循环填充:
三、 池化
与卷积层相似,池化层负责减小卷积特征的空间大小。这是通过减小尺寸来减少处理数据所需的计算能力。平均池化和最大池化有两种类型。
(1) 最大池化层
如图所示,使用的是步长为2,最大池化的滤波器为2,进行最大池化的效果,最大池化是指选择滤波器中最大值,作为输出。
(2) 平均池化层
如图所示,使用的是步长为2,平均池化的滤波器为2,进行平均池化的效果,平均池化是指对滤波器中的值做平均,再作为输出。
四、 典型的卷积网络结构
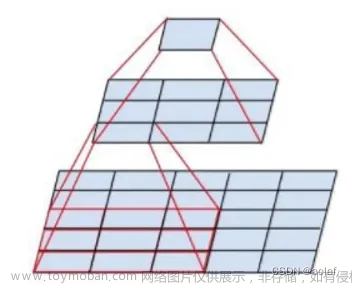
输入一张单通道的图像,我们通过三个卷积核对图像做卷积,获得到三张不同的图像,包含的图像特征也不一样,在经过池化,减少图像的尺寸,在进行激活函数,最后在输出,以此类推,当我们做完卷积后,将所有获得的图像特征数据,进行拉伸成一个向量,在放入全连接神经网络中,进行我们的预测、分类等相关任务
五、 多通道进行卷积
当我们输入为图像为多通道,输出也为多通道,加上偏执bias的情况
我们想输出多少个通道,就要多少个卷积滤波器
如图所示,当我们的输入为三通道图像,卷积滤波器的步长为2,尺寸为3x3,我们想要输出为两个通道的图像时,我们就需要2个卷积滤波器,卷积滤波器里的卷积核数量与输入通道的数量一致。
一个卷积滤波器在做卷积计算时,每一个通道都有对应的卷积核,通过卷积计算后,我们能得到通道数量的图像,再将全部图像对应的像素一一进行累加,再加上偏执,最终输出成一张图像。
当我们有两个滤波器时,那么输出就会输出两个通道图像。
六、 卷积神经网络与普通神经网络的区别
卷积层的特征:
(1) 利用了图像的局部像素间的相关性
假设我们需要识别一个图片是否有一只猫,那么无论这只猫在图片的什么位置,我们都应该识别出来。
如图所示,只要红色的框的在图像内,不管他在图像什么位置,我们都应该识别出来猫,我们识别猫时,只用了局部像素的相关性(红色的框),而不像全连接神经网络一样,对每一个像素之间做计算。
如图所示,最左边的普通神经网络的计算,每一个神经元都需要和全部的像素做计算,而卷积神经网络(中间和右边图像),每一个神经元只与做卷积的像素有关系,与其他的像素没有关系
(2) 减少了网络系数数量(降低了模型复杂度),避免了过拟合
七、 卷积的严格定义
八、 卷积公式
卷积网络的卷积操作,是将卷积核旋转180度后,才进行的卷积操作。
数学上的卷积公式是Convolution,但我们希望卷积时,能像Corss-correlation一样,所以需要将卷积核旋转180度,在进行Corss-correlation卷积。
九、 卷积神经网络的前向传播

卷积神经网络同一层的卷积都使用同一个卷积核。与普通的神经网络不同,普通的神经网络同一层对于下一层的每个神经元都有自己的不同权重W。
十、 卷积神经网络的反向传播
(1) 损失函数对卷积核的梯度
当我们想对卷积核中的黄色部分值,进行梯度求导,那么梯度求导过程如下
我们设置的卷积步长,还有对图像是否padding对卷积操作有影响,所以在进行反向传播时,也要考虑这些因素,上图的求导,是卷积步长为1,不做padding下,进行的求导
损失函数想对卷积核其中的一个值进行梯度求导时,因为依赖关系,卷积核梯度依赖损失函数对输出的值,输出值在对卷积核进行梯度求导。
因为反向传播,所以卷积核梯度依赖损失函数对输出的值是已知的,所以只需要求输出值在对卷积核得梯度即可
对卷积核其中一个值进行梯度求导时,只关注图像进行卷积时,图像的像素值与卷积核中的值进行卷积后,得出值。其余的不关注
最终求导的出为输入的O值
最终公式如下:
(2) 损失函数对特征图的梯度
因为卷积是只对像素点局部区域进行的,如紫色图所示,一个像素点只会影响局部区域,所以想对输入的图像像素值进行梯度求导时,过程如下
损失函数相对图像中的某一个像素点p进行梯度求导,根据反向传播求导的依赖关系,等于损失函数对受p像素点影响,进行卷积后的输出值进行求导,这部分是已知的,再由受影响的输出值,对p像素进行求导
受p像素影响的输出值,对p像素进行求导如下:

p像素作为输入时,是做了激活函数再输入,所以在最终求导过程中,也包含对应的激活函数
在对p像素求导时,因为卷积时,只对像素的局部进行的,所以我们梯度求导时也只关注p像素做卷积后输出的值,其余的不关心
最终求导公式如下:

十一、 卷积的各种变形
(1) 普通的卷积(Conv2D)
步长为1,卷积核尺寸为3x3,图像padding的
步长为1,卷积核尺寸为3x3,图像不做padding的
(2) 膨胀卷积(Dilated/Atrous Conv2D)

(3) Transposed Convolution
(4) 卷积分解 文章来源:https://www.toymoban.com/news/detail-463725.html
文章来源:https://www.toymoban.com/news/detail-463725.html
将一个3x3的卷积进行分解,卷积参数可以从原本的9个参数,变成6个参数,计算量比原本的卷积小。文章来源地址https://www.toymoban.com/news/detail-463725.html
到了这里,关于CNN卷积神经网络的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!