目录
前言
1.联和仿真函数介绍
1.1 assignin函数
1.2 sim函数
1.3 feval函数
2.使用粒子群算法优化simulink模型中的PID调节参数
2.1实现程序
2.2仿真结果
3.使用遗传算法优化simulink模型中的PID调节参数
3.1实现程序
3.2仿真结果
4.总结
前言
上几篇文章我们介绍了用常规遗传算法以及其工具箱、粒子群算法求多目标或者多元函数的最大值或者最小值问题,这篇文章将介绍如何利用优化算法与simulink联合仿真,优化控制中需要调节的参数问题。
由于手动调参会非常麻烦,而且即使调节效果较好也难以找到全局最优解,所以非常有必要去使用优化算法全局寻优的能力进行自动调参,本篇文章以典型的PID调参为例进行介绍。其关键的地方在于:①如果在simulink建模,如何实现优化算法与simulink的联合仿真②选择适当的性能指标,或者说目标函数。
1.联和仿真函数介绍
与simulink联合仿真,常见的操作是在matlab命令行语句控制simulink的仿真和优化算法的迭代,当然也可以用s函数将优化算法编写到simulink模块,本文采样前一种,所以有必要介绍其中重要的两个函数。
1.1 assignin函数
作用:为指定工作区中的变量赋值
格式:assignin(ws,var,val) 将值 val 赋给工作区 ws 中的变量 var。
例如,assignin('base','x',42) 将值 42 赋予 MATLAB® 基础工作区中的变量 x。
1.2 sim函数
-
批量仿真
当Simulink模型已经固定下来需要调参或者需要批量仿真的时候,循环语句+sim()函数能够轻松实现这个目标,而且还可以使数据自动导出保存。 -
参数优化
这其实已经是以函数的方式调用simulink模型了,这样的话,MATLAB一众的优化函数自然就能够用上了 -
性能提升
使用函数调用以后,仿真的时间是能够降下去的,主要是因为图形界面的开销没有了
格式:[T,X,Y1,...,Yn] =sim('model',Timespan, Options, UT)

更详细的介绍可以官方help文档。
参考链接:
[Matlab] Simulink用得多了,不知道sim()函数你又知多少? - 知乎
对 Simulink 模型进行仿真 - MATLAB sim- MathWorks 中国
1.3 feval函数
[y1,...,yN] = feval(fun,x1,...,xM) 使用函数的名称或函数句柄以及输入参数 x1,...,xM 来计算函数的结果。
如:
示例: fun = 'cos'
示例: fun = @sin
再例如以下是等价的:
fh = @eig; [V,D] = fh(A) [V,D] = feval(@eig,A)
2.使用粒子群算法优化simulink模型中的PID调节参数


2.1实现程序
这里假设粒子搜索的P、I、D三个维度/变量上下限不一样(虽然设置的一样),它的初始化方法会于单变量函数不同,读者可以细细体会。
对于同一个程序求同一个目标函数的最大值或者最小值有两种方法,一种是将适应度函数取反或者倒数,这样处理后,最优解=群体最佳适应度的相反数或者倒数;第二种是采用相同的适应度函数,但是位置和速度更新上会有变化,详细可以查看我的上篇文章,详细介绍了如何用同一程序稍加改动即可实现求解同一目标函数的最大值和最小值。
上篇文献链接:
粒子群算法PSO求解最大值和最小值案例(超详细注释)_Mr. 邹的博客-CSDN博客
优化性能(ITAE)指标:

注:对于这种性能指标只是最小化即可,实际上很多优化问题还会有约束条件,后面会慢慢学习并与大家分享。
本篇文章的粒子群优化PID参数程序
目标函数:
function z=PSO_PID(x)
assignin('base','Kp',x(1));
assignin('base','Ki',x(2));
assignin('base','Kd',x(3));
[t_time,x_state,y_out]=sim('PID_Model',[0,10]);
z=y_out(end,1);2.2仿真结果
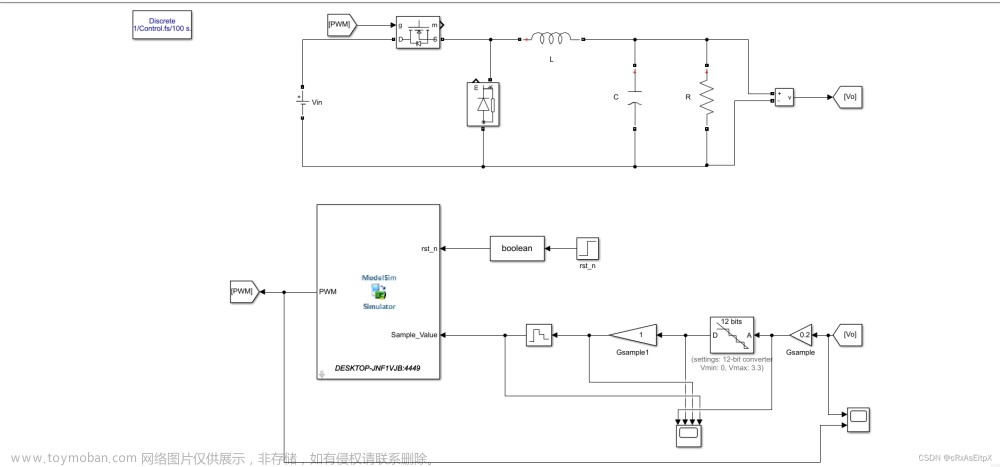
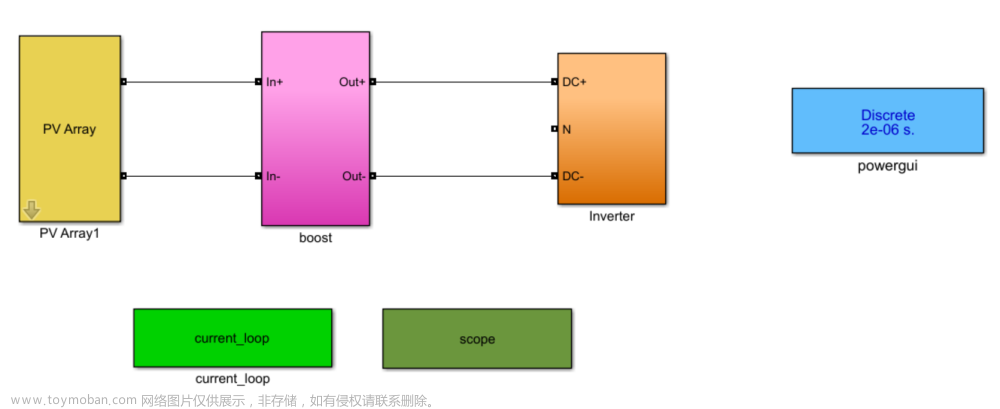
以简单的被动对象为传递函数,跟踪单位阶跃曲线,模型如下:

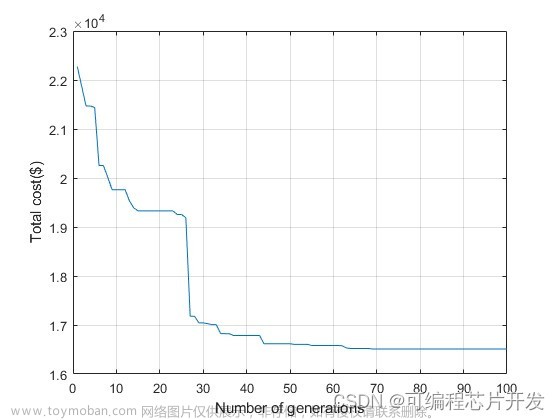
由于是求最小值,而取目标函数为适应度函数,所以适应度是呈下降的趋势;由于这里PID优化参数中i的变化很小,为了展示其优化的过程,所以将PID3个参数的优化值分别拿出来展示。





3.使用遗传算法优化simulink模型中的PID调节参数
这里直接使用遗传算法库函数GA进行优化,推荐大家去看我下面这篇文章,有关于库函数GA和工具箱的详细使用案例:
遗传算法、遗传算法库函数ga和gamultiobj、遗传算法工具箱GADS实例介绍_Mr. 邹的博客-CSDN博客
3.1仿真结果

4.总结
①对于这样在matlab界面仿真分析,实际上每次优化simulink模型都会运行一次,如果模型稍复杂些,可能运行时间会很长,所以还有其他的方法,后续会进行学习与大家分享。
②对于粒子群算法而言Kp、Ki、Kd三个变量参数其实就是一个粒子的三个维度,或者说三个搜索的最优位置坐标,而适应度值即为最小化的ITAE性能指标文章来源:https://www.toymoban.com/news/detail-463951.html
注:由于本人也是在不断地学习期间,所以如果文章中有什么错误,欢迎大家指正批评,谢谢!文章来源地址https://www.toymoban.com/news/detail-463951.html
到了这里,关于PSO、GA与simulink模型联合仿真分析(超详细算法解析)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!