[入门必看]数据结构6.1：图的基本概念

10月前作者：H3T 分类：Toy博客阅读(43) 违法举报

这篇具有很好参考价值的文章主要介绍了[入门必看]数据结构6.1：图的基本概念。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

第六章图

小题考频：33
大题考频：11

6.1 图的基本概念

难度：☆☆☆☆

知识总览

6.1.1 图的基本概念

[入门必看]数据结构6.1：图的基本概念

6.1.1 图的基本概念

图的定义

[入门必看]数据结构6.1：图的基本概念

A、B、C……这些元素的集合就是顶点集V，图G中顶点个数也成为图G的阶；
连接各个顶点的边的集合就是边集E

注意。图里面的一条边，连接的u,v两个顶点必须是刚才给出的顶点集中的顶点，边的两头必须连着顶点。

一个图的顶点集不可以为空，边集可以为空

图逻辑结构的应用

[入门必看]数据结构6.1：图的基本概念

无向图、有向图

[入门必看]数据结构6.1：图的基本概念

无向边，简称边；有向边，简称弧。

无向边(v,w)=(w,v)这两种表述方式是等价的；
有向边<v,w>≠<w,v>是不等价的，方向刚好相反。
有向边<v,w>，v称为弧尾，w称为弧头，弧尾是没有箭头的这一边，弧头是有箭头的这一边

用集合的方式表示左边的无向图：

此处用圆括号表示一条边

用集合的方式表示右边的有向图：

此处用尖括号表示弧，如果弧的两个元素位置互换，表示两个相反的弧

简单图、多重图

[入门必看]数据结构6.1：图的基本概念

简单图：不存重复边和顶点连向自身的边
数据结构教程中默认探讨“简单图”

因为绝大多数问题都可以用简单图来解决：
[入门必看]数据结构6.1：图的基本概念

思考，如何描述社交达人、微博大V、吃瓜指数呢？

研究连接一个结点的边有多少条是一个有现实意义的事情。

顶点的度、入度、出度

[入门必看]数据结构6.1：图的基本概念

无向图：
顶点v的度：依附于顶点v的边的条数

有向图：
入度：以v为终点的有向边的条数
出度：以v为起点的有向边的条数
顶点v的度：入度和出度之和

无向图：
全部顶点度之和=边数2倍

有向图：
入度之和=出度之和=弧的条数

顶点-顶点的关系描述

[入门必看]数据结构6.1：图的基本概念

路径：两个顶点之间的路径，指的就是顶点序列。有向图中路径方向要与弧的方向一致。
回路：第一个顶点和最后一个顶点相同的路径称为回路或环。
简单路径：路径序列中，顶点不重复出现。
简单回路：除第一个顶点和最后一个顶点外，其余顶点不重复出现。
路径长度：路径上边的数目
点到点的距离：最短路径称为距离，若不存在路径，记距离为无穷（∞）。

无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的
有向图中，若从顶点v到顶点w和从顶点w到顶点v之间都有路径（有正向也有逆向），则称这两个顶点是强连通的

连通图、强连通图

[入门必看]数据结构6.1：图的基本概念

对于n个顶点的无向图G，
若G是连通图，则最少有 $n - 1$ 条边
若G是非连通图，则最多可能有 $C_{n-1}^{2}$ 条边，如果多加一条边，该图就会变为连通图。

对于n个顶点的有向图G，
若G是强连通图，则最少有n条边（形成回路）

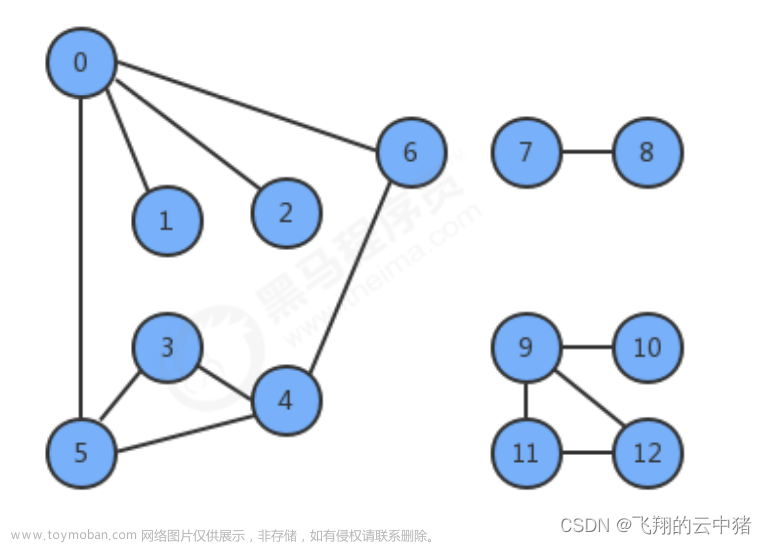
研究图的局部——子图

[入门必看]数据结构6.1：图的基本概念

子图首先是一个图
生成子图：包含子图中所有顶点的子图

[入门必看]数据结构6.1：图的基本概念

连通分量

[入门必看]数据结构6.1：图的基本概念

无向图中的极大连通子图称为连通分量。
连通：每一个连通分量都是原图的一个子图，并且这些子图都是连通的。
极大：子图中包含尽可能多的顶点和尽可能多的边

[入门必看]数据结构6.1：图的基本概念

强连通分量

[入门必看]数据结构6.1：图的基本概念

有向图中的极大强连通子图称为强连通分量。
连通：每一个强连通分量都是原图的一个子图，并且这些子图都是强连通的。
极大：子图中包含尽可能多的顶点和尽可能多的边

生成树

[入门必看]数据结构6.1：图的基本概念

生成树：无向图中包含全部顶点的一个极小连通子图，边尽可能地少。
顶点树为n

生成森林

[入门必看]数据结构6.1：图的基本概念

将非连通图生成连通分量

[入门必看]数据结构6.1：图的基本概念

将连通分量生成对应的生成树

生成树的应用：修路，给多种方案选最好的。

哪个最好？看每条路的成本……

边的权、带权图/网

[入门必看]数据结构6.1：图的基本概念

边的权：在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值。
带权图/网：边上带有权值的图称为带权图，也称网。

带权路径长度：当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度

带权图的应用举例

[入门必看]数据结构6.1：图的基本概念

几种特殊形态的图

[入门必看]数据结构6.1：图的基本概念

无向完全图：无向图中任意两个顶点之间都存在边
若无向图的顶点数|V|=n，则 |E| ∈ [ $0, C_{n}^{2}$ ] = [ 0, n(n–1)/2 ]

有向完全图：有向图中任意两个顶点之间都存在方向相反的两条弧
若有向图的顶点数|V|=n，则|E| ∈ [ $0,2C_{n}^{2}$ = [ 0, n(n–1) ]

[入门必看]数据结构6.1：图的基本概念

一般来说|E| < |V|log|V|时，可以将G视为稀疏图

[入门必看]数据结构6.1：图的基本概念

树：不存在回路，且连通的无向图
若|E|>n-1，则一定有回路

有向树：一个顶点的入度为0（根结点）、其余顶点的入度均为1的有向图，称为有向树。

知识回顾与重要考点

6.1.1 图的基本概念

[入门必看]数据结构6.1：图的基本概念

常见考点：
对于n个顶点的无向图G，

所有顶点的度之和=2|E|
若G是连通图，则最少有n-1条边（树），
若|E|>n-1，则一定有回路
若G是非连通图，则最多可能有 $C_{n-1}^{2}$ 条边
无向完全图共有 $C_{n}^{2}$ 条边

对于n个顶点的有向图G，文章来源地址https://www.toymoban.com/news/detail-464522.html

所有顶点的出度之和=入度之和=|E|
所有顶点的度之和=2|E|
若G是强连通图，则最少有n条边（形成回路）
有向完全图共有条 $2C_{n}^{2}$ 边

到了这里，关于[入门必看]数据结构6.1：图的基本概念的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

【数据结构与算法】图的基本概念 | 邻接矩阵和邻接表 | 广度优先遍历和深度优先遍历

🌠 作者：@ 阿亮joy. 🎆 专栏：《数据结构与算法要啸着学》 🎇 座右铭：每个优秀的人都有一段沉默的时光，那段时光是付出了很多努力却得不到结果的日子，我们把它叫做扎根图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E) ，其中：顶点集合V = {x|x属于某

2024年02月04日
浏览(73)
图的数据结构，系统学习图的基本概念、定义和建立，学会邻接矩阵、邻接表以及实现六度空间案例，遍历图的方式——广度、深度访问

图：G = (V,E) Graph = (Vertex, Edge) V：顶点（数据元素）的有穷非空集合； E：边的有穷集合。有向图：每条边都是有方向的无向图：每条边都是无方向的完全图：任意两点之间都有一条边相连无向完全图：n个顶点，n(n-1)/2条边无向完全图：n个顶点，n(n-1)条边稀疏

2023年04月22日
浏览(48)
【数据结构入门】-二叉树的基本概念

个人主页：平行线也会相交欢迎点赞👍 收藏✨ 留言✉ 加关注💓本文由平行线也会相交原创收录于专栏【数据结构初阶（C实现）】今天的内容可是一个大头，比以往学的内容上了一个档次。大家对于这块内容一定要好好学，不是很理解的地方一定要及时解决，要不然到

2023年04月10日
浏览(82)
数据结构——图的基本定义以及图的存储结构，邻接矩阵，邻接表

目录图的定义和术语图的存储结构顺序存储结构—邻接矩阵链式存储结构邻接表邻接多重表十字链表图的遍历图的连通性问题有向无环图及其应用最短路径图的定义：图是一种非线性的复杂的数据结构，图中的数据元素的关系是多对多的关系，在图中我们常常把数

2024年02月04日
浏览(58)
数据结构（入门必看）

1、学习C语言是如何写程序,学习数据结构如何简洁高效的写程序 2、遇到一个实际问题，需要写程序，需要解决两个方面的问题 1)如何表达数据之间的逻辑规律以及如何将数据存储到计算机中数据结构数据：不是单纯的数值，而是一个类似于集合的概念（结构体（节点））

2024年02月02日
浏览(37)
【数据结构】图的基本操作

一、问题描述分别以邻接矩阵和邻接表作为存储结构，实现以下图的基本操作：增加一个新结点v，Insert(G,v)；删除顶点v及其相关的边，Delete(G,v)；增加一条边v,w，Insert(G,v,w)；删除一条边v,w，Delete(G,v,w)；二、设计思路 1、邻接矩阵实现：邻接矩阵实现图的基本

2024年02月06日
浏览(50)
数据结构--图的基本操作

使用的存储模式：图的基本操作： • Adjacent(G,x,y)：判断图G是否存在边x, y或(x, y)。 • Neighbors(G,x)：列出图G中与结点x邻接的边。 • InsertVertex(G,x)：在图G中插入顶点x。 • DeleteVertex(G,x)：从图G中删除顶点x。 • AddEdge(G,x,y)：若无向边(x, y)或有向边x, y不存在，则向图G中添加该

2024年02月16日
浏览(53)
[入门必看]数据结构5.4：树、森林

小题考频：30 大题考频：8 难度：☆☆☆ 5.4.1 树的存储结构 5.4.2 树、森林与二叉树的转化 5.4.3 树和森林的遍历树的逻辑结构树是一种递归定义的数据结构一棵树要么是空树，要么至少有一个根结点，根结点的下方可能有零棵或多棵互不相交的子树。二叉树：一个分支结点

2024年02月03日
浏览(43)
[入门必看]数据结构4.2：串的模式匹配

小题考频：2 大题考频：0 难度：☆☆☆☆☆ 4.2.1_朴素模式匹配算法 4.2.2_1_KMP算法 4.2.2_2_求next数组 4.2.3_KMP算法的进一步优化什么是字符串的模式匹配 ——在字符串内搜索某一段内容查找功能搜索引擎字符串模式匹配：在主串中找到与模式串相同的⼦串，并返回其所在位置

2023年04月23日
浏览(40)
算法与数据结构（十）--图的入门

图是由一组顶点和一组能够将两个顶点连接的边组成的。按照连接两个顶点的边的不同，可以把图分为以下两种：无向图：边仅仅连接两个顶点，没有其他含义；有向图：边不仅连接两个顶点，并且具有方向; 另外图还可以分为赋权图和非赋权图，一个是每条边都带有权值

2024年02月11日
浏览(43)