目录
一.引言
二.计算流程
1.Attention 结构
2.Multi-Head Attention 结构
三.计算实现
1.Item、序列样本生成
2.OwnAttention Layer 实现
2.1 init 初始化
2.2 build 参数构建
2.3 call 逻辑调用
3.OwnAttention Layer 测试
四.总结
一.引言
Attention And Multi-Head Attention 一文中我们简单介绍了 Attention 与 Multi-Head Attention 在推荐场景下的计算,本文通过 Keras 自定义 Layer 的方式,实现 OwnAttention Layer 实现两种 Attention 的功能。
二.计算流程
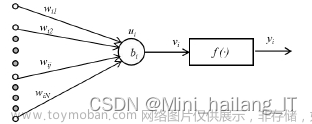
1.Attention 结构

• 输入
Query 为候选 Item
Keys 为用户行为序列 Goods id,key_i 代表第 i 个行为 good
Values 与 Keys 相同
• 计算
lookup 获取 query、keys、values 向量
query 向量 + keys 向量通过 ActivationUnit 获取每个 key_i 对应的权重 weight_i
weight_i softmax 归一化,此步骤可选
将 weight_i 与 value_i 加权平均得到 Attention Output
2.Multi-Head Attention 结构

• 输入
Query 为候选 Item
Keys 为用户行为序列 Goods id,key_i 代表第 i 个行为 good
Values 与 Keys 相同
• 计算
lookup 获取 query、keys、values 向量
原始向量先经过一次 Linear 层
根据 head 的数量,将向量 Split 分为多个子向量,代表不同子空间
每一个 Head 下的子向量执行 Scaled Dot-Product Attention 得到权重 Weight
与子空间 Value 加权平均得到输出
输出再通过一次 Linear 层并 Concat 得到 Attention Output
三.计算实现
1.Item、序列样本生成
def genSamples(_batch_size=5, _T_k=10, _N=1000, seed=0):
np.random.seed(seed)
# 用户历史序列
user_history = np.random.randint(0, N, size=(batch_size, _T_k))
# 候选 Item
user_candidate = np.random.randint(0, N, size=(batch_size, 1))
return user_history, user_candidatebatch_size 为样本数,T_k 为行为数,N 为 Goods 总数,模拟数据,主要为了跑通逻辑:
# 用户历史行为序列 && 候选商品 ID
batch_size, T_k, N = 5, 10, 1000
history, candidate = genSamples(batch_size, T_k, N)
print(history[0:5])
print(candidate[0:5])
2.OwnAttention Layer 实现
2.1 init 初始化
import numpy as np
import tensorflow as tf
from tensorflow.python.keras.layers import *
from tensorflow.keras.layers import Layer
class OwnAttention(Layer):
def __init__(self, _mode='Attention', _is_weight_normalization=True, **kwargs):
self.activation_unit = None
self.DNN = None
self.LastDNN = None
self.kernel = None
self.N = 10000
self.T_k = 10
self.emd_dim = 8
self.num_heads = 2
self.mode = _mode
self.is_weight_normalization = _is_weight_normalization
super().__init__(**kwargs)N、T_k、emd_dim 分别代表商品库大小、序列长度与向量维度
mode 供分两种 'Attention' 与 'Multi-Head Attention' 分别代表两种 Attention 模式
is_weight_normalization 权重是否归一化,这个根据自己场景与内积的量纲决定
2.2 build 参数构建
def build(self, input_shape):
# 获取 Item 向量
self.kernel = self.add_weight(name='seq_emb',
shape=(self.N, self.emd_dim),
initializer='he_normal',
trainable=True)
# Multi-Head Linear
self.DNN = Dense(self.emd_dim, activation='relu')
self.LastDNN = Dense(self.emd_dim, activation='relu')
# Activation Unit
self.activation_unit = Dense(1, activation='relu')
super(OwnAttention, self).build(input_shape)kernel 为商品 id 对应的 Embedding 层,维度为 N x emd_dim
DNN 为 Multi-Head 的首层 Linear
LastDNN 为 Multi-Head 的末层 Linear
activation_unit 用于计算加权权重
Tips:
关于 activation_unit,除了上面的简单实现外,还可以加入 goods 对应的 Position Embedding 或者加入其它 SideInfo 侧信息辅助决策。
2.3 call 逻辑调用
def call(self, inputs, **kwargs):
_history, _candidate = inputs
Q = tf.nn.embedding_lookup(self.kernel, _candidate)
K = tf.nn.embedding_lookup(self.kernel, _history)
V = tf.nn.embedding_lookup(self.kernel, _history)
print("Q Shape: %s \nK Shape: %s \nV Shape: %s" % (Q.shape, K.shape, V.shape))第一步 lookup 获取 id 对应的 Embedding,BS=5、T_k=1、emd_dim=8:
Q Shape: (5, 1, 8)
K Shape: (5, 10, 8)
V Shape: (5, 10, 8)• mode = 'Attention'
if self.mode == 'Attention':
# 获取 Attention 权重
# [None, T_k, emd_dim] -> [None, T_k, 1] -> [None, 1, T_k]
din_out = self.activation_unit(K)
din_out = tf.transpose(din_out, (0, 2, 1))
# 构建 Mask [None, 1, T_k]
seq_mask = tf.equal(_history, tf.zeros_like(_history))
seq_mask = tf.expand_dims(seq_mask, axis=1)
# 权重归一化, 权重不使用 softmax 归一化则默认为 0 填充 [None, 1, T_k]
if self.is_weight_normalization:
paddings = tf.ones_like(din_out) * (-2 ** 32 + 1)
else:
paddings = tf.zeros_like(din_out)
# 归一化 + Padding 的 Attention 权重 [None, 1, T_k]
din_out = tf.where(seq_mask, paddings, din_out)
if self.is_weight_normalization:
din_out = tf.nn.softmax(din_out, axis=2)
# Attention 输出
output = tf.matmul(din_out, V)
output = tf.squeeze(output)
return output计算逻辑与维度可参考上面的文字注释,这里增加了 padding 与 weight_normalization,din_out 为最终的加权权重,V 为 values 即 lookup 得到的序列 Embedding。
• mode = 'Multi-Head Attention'
elif self.mode == 'Multi-Head Attention':
# Linear
Q = self.DNN(Q) # [None, T_q, emd_dim]
K = self.DNN(K) # [None, T_k, emd_dim]
V = self.DNN(V) # [None, T_k, emd_dim]
# Split And Concat
Q_ = tf.concat(tf.split(Q, self.num_heads, axis=2), axis=0) # [h*None, T_q, emd_dim/h]
K_ = tf.concat(tf.split(K, self.num_heads, axis=2), axis=0) # [h*None, T_k, emd_dim/h]
V_ = tf.concat(tf.split(V, self.num_heads, axis=2), axis=0) # [h*None, T_k, emd_dim/h]
# Scaled Dot-Product
# [h*None, T_q, emd_dim/h] x [h*None, emd_dim/h, T_k] -> [h*None, T_q, T_k]
d_k = Q_.shape[-1]
weight = tf.matmul(Q_, tf.transpose(K_, [0, 2, 1]))
weight = weight / (d_k ** 0.5)
weight = tf.nn.softmax(weight)
# Weighted-Sum
# [h*None, T_q, T_k] * [h*None, T_k, emd_dim/h] -> [h*None, T_q, emd_dim/h]
weighted = tf.matmul(weight, V_)
print("Weight Shape: %s Value Shape: %s Weighted-Sum Shape: %s" % (weight.shape, V_.shape, weighted.shape))
# Concat && Linear
# [None, T_q, emd_dim]
concat = tf.squeeze(tf.concat(tf.split(weighted, self.num_heads, axis=0), axis=2))
multiHeadOutput = self.LastDNN(concat)
return multiHeadOutputSplit 负责根据 head 数量将原始向量拆分为多个向量子空间,d_k 为缩放系数,这个可以根据自己场景决定,与上面 Attention 不同的是前后增加了两个 Linear 层,除此之外,实际应用时这里可能还需要 Paddiing 与 Dropout。
3.OwnAttention Layer 测试
• mode = 'Attention'
mode = 'Attention'
attention = OwnAttention(mode)
attention_output = attention([history, candidate])
print("%s Output Shape: %s" % (mode, attention_output.shape))Attention Output Shape: (5, 8)• mode = 'Multi-Head Attention'
mode = 'Multi-Head Attention'
attention = OwnAttention(mode)
attention_output = attention([history, candidate])
print("%s Output Shape: %s" % (mode, attention_output.shape))Weight Shape: (10, 1, 10) Value Shape: (10, 10, 4) Weighted-Sum Shape: (10, 1, 4)
Multi-Head Attention Output Shape: (5, 8)四.总结
实现的比较简单,主要是粗略了解 Attention 与 Multi-Head Attention 的实现流程,实际应用场景下,如果 Goods 商品库的 N 太大,也可以采用 Hash 的方式,在牺牲一定性能的情况下弥补工程上的不足。文章来源:https://www.toymoban.com/news/detail-464685.html
更多推荐算法相关深度学习:深度学习导读专栏 文章来源地址https://www.toymoban.com/news/detail-464685.html
到了这里,关于深度学习 - 51.推荐场景下的 Attention And Multi-Head Attention 简单实现 By Keras的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!