【数学建模】混合整数规划MIP（Python+Gurobi代码实现）

这篇具有很好参考价值的文章主要介绍了【数学建模】混合整数规划MIP（Python+Gurobi代码实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1 概述

2 入门算例

2.1 算例

2.2 求解 ——Pulp库和cvxpy

3 进阶算例

3.1 算例

3.2 Python+Gurobi代码实现

3.3 运行结果

1 概述

混合整数规划 (MIP) 是 NP-hard 问题中的一类，它的目标是在线性约束下将线性目标最小化，同时使部分或全部变量均为整数值，在容量规划、资源分配与装箱等等现实场景中得到了广泛应用。

该方向的大量研究与工程投入都集中在了开发实用求解器上，比如 SCIP、CPLEX、Gurobi 和 Xpress。这些求解器都是使用复杂的启发式算法来指导求解 MIP 的搜索过程。一个求解器在特定应用上的表现主要是取决于该求解器的启发式算法与该应用的匹配程度。

1）整数规划（Integer Programming,简称IP）:规划问题中一部分变量或者全部变量为整数变量的话，该数学规划问题就属于整数规划问，即自变量存在整数。
2）整数规划的可行域是离散的
3）整数规划问题被看作数学规划里、乃至世界上最难的问题之一，通常退而求其次求解近似解或局部最优解。
4）常见整数规划问题：背包问题、广义指派问题、集合覆盖问题
5）分类（按决策变量分）：
①全部决策变量限制为整数的规划问题，称为纯整数规划
②部分决策变量限制为整数的规划问题，称为混合整数规划，即自变量既包含整数也有连续变量，混合整数规划(mixed integer programming,简称MIP）基础：https://www.gurobi.com/resource/mip-basics/
③决策变量只取0或1的规划问题，称为0-1整数规划

求解
1）求解难度大：虽然连续优化问题的可行解有无数多个，但是通过微积分，这一成熟且强大的工具，往往可以建立出针对连续优化（即可微）问题的最优性条件。整数规划问题中，整数不连续从而不可微分，导致无法使用微积分的工具，难以得到最优性条件，同时由于离散，无法满足凸性。
2）普遍方法：
① 整数规划方法：分支定界法、割平面法、蒙特卡罗法、列生成法，拉格朗日松弛法等
② 0-1整数规划：隐枚举法、（指派问题：匈牙利法）

3）精确算法：分支定界法(Branch and Bound Algorithm, B&B)、枚举法
分支（Branching) 算法是整数规划求解器的核心框架
整数规划精确算法核心的便是分支定界法，以及增加分支定界效率的各种技巧，例如割平面方法（Cutting Planes Method）。

①问题的规模往往非常小；②最后获得的解，必定是最优解

4）近似算法（Approximate Algorithm）:
根据特定问题使用一些技巧（贪婪策略，限制，划分，断切，松弛）
比较考验技术，需要给出算法的近似比，复杂度分析，具有很强的推理能力。同样，这类算法的求解规模还是比较受限制的，其最后获得的解不是最优解。

5）启发式算法（Heuristic Algorithm）:算法设计者根据经验或者观察到的性质设计出来的。TSP问题：LKH算法。
启发式算法大致可以分为四类：取整（Rounding）、下潜（Diving）、子问题（Sub-MIP）和上述三类之外的其他算法。

也可以参考这个博主的文章，讲解比较好：

整数规划（Python)

2 入门算例

2.1 算例

【数学建模】混合整数规划MIP（Python+Gurobi代码实现）

2.2 求解 ——Pulp库和cvxpy

代码：整数规划（Python)

3 进阶算例

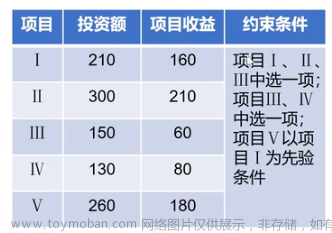
3.1 算例

模型中共有个变量，即:

本次以十行十列的矩阵为例：

3.2 Python+Gurobi代码实现

# # -*- coding: utf-8 -*-

'''
1) 一次声明多个变量；

2) 一次写出多个约束'''

from gurobipy import *
import numpy as np

N_i=10
N_j=10

# 创建模型
MIP=Model("N-Queen")  #N维矩阵

# 变量声明
OP =MIP.addVar(lb=0,ub=GRB.INFINITY, name="OP")
x  =MIP.addVars(N_i,N_j,vtype=GRB.BINARY, name="x")  #addVars，多个变量记得加s

'''在Gurobi中主要用到的变量类型 vtype=

GRB.CONTINUOUS——连续变量（Gurobi默认变量类型，可以省略）

GRB.BINARY——二进制变量（0-1）

GRB.INTEGER——整数变量（1,2,3,10,5等整数）

'''
# 设置目标函数
MIP.setObjective(quicksum(x[i,j] for i in range(N_i) for j in range(N_j)),GRB.MAXIMIZE)

# 添加约束
''''sum(x[ij] for j in range(N_j))'——对x[ij]中每一行进行求和'''
MIP.addConstrs((sum(x[i,j] for j in range(N_j))<=1 for i in range(N_i)),"Con1")
MIP.addConstrs((sum(x[i,j] for i in range(N_i))<=1 for j in range(N_j)),"Con2")


# # 防止0-1变量带有小数位
MIP.Params.IntegralityFocus=1

# Optimize model
MIP.optimize()

MIP.write("N-Queen.lp")

'''汇总解集'''
x_c=np.zeros((N_i,N_j))
for i in range(N_i):
    for j in range(N_j):
        print(i)
        x_c[i,j]=x[i,j].x

print('**************')
print(' ======最优解为========== ')
print('**************')
print('目标函数为 :',MIP.ObjVal) # 输出目标值
print('x解得 :',x_c) # 输出 X 的值

3.3 运行结果

Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (win64)
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads
Optimize a model with 2 rows, 3 columns and 4 nonzeros
Model fingerprint: 0x8d1a4e8d
Variable types: 1 continuous, 2 integer (2 binary)
Coefficient statistics:
  Matrix range     [1e+00, 3e+00]
  Objective range  [1e+00, 4e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [3e+00, 8e+00]
Found heuristic solution: objective 5.0000000

Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 1 (of 16 available processors)

Solution count 1: 5 

Optimal solution found (tolerance 1.00e-04)
Best objective 5.000000000000e+00, best bound 5.000000000000e+00, gap 0.0000%
输出名为‘LP_Expression’的 .lp文件
=========================
====最优解为========
===========================
OP is : 5.0
x1 is : 1.0
x2 is : 1.0

Process finished with exit code 0

Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (win64)
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads
Optimize a model with 2 rows, 3 columns and 4 nonzeros
Model fingerprint: 0x8d1a4e8d
Variable types: 1 continuous, 2 integer (2 binary)
Coefficient statistics:
Matrix range [1e+00, 3e+00]
Objective range [1e+00, 4e+00]
Bounds range [1e+00, 1e+00]
RHS range [3e+00, 8e+00]
Found heuristic solution: objective 5.0000000

Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 1 (of 16 available processors)

Solution count 1: 5

Optimal solution found (tolerance 1.00e-04)
Best objective 5.000000000000e+00, best bound 5.000000000000e+00, gap 0.0000%
输出名为‘LP_Expression’的 .lp文件
=========================
====最优解为========
===========================
OP is : 5.0
x1 is : 1.0
x2 is : 1.0

Process finished with exit code 0
文章来源地址https://www.toymoban.com/news/detail-464732.html

到了这里，关于【数学建模】混合整数规划MIP（Python+Gurobi代码实现）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！