【计算几何】判断多边形边界顺逆时针 & C++代码实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了【计算几何】判断多边形边界顺逆时针 & C++代码实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

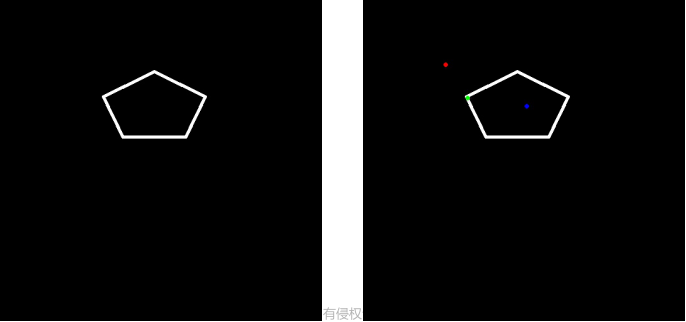
一、多边形边界顺序

多边形可以由一个点集 ${v_1,v_2,...,v_n\}$ 表示，构成多边形的点集确定，多边形边界的顺序也就确定了

有关多边形边界的顺序的示意图，如下图所示：

【计算几何】判断多边形边界顺逆时针 & C++代码实现

有时候关于数据格式有规定，要求多边形边界必须为顺时针或者逆时针。

因此，我们需要对多边形边界的顺序进行判断，如果不符合要求，则需要将构成多边形的点集进行反转

二、数学原理

2.1 Green公式

Green公式揭示了平面区域的二重积分和封闭曲线上的线积分的关系：沿着多边形的边求曲线积分,若积分为正,则是沿着边界曲线正方向(逆时针),反之为顺时针,且所得绝对值为多边形面积

判断多边形是逆时针还是顺时针，就更简单了，直接计算多边形面积（不取绝对值）：

如果面积为正值，是逆时针；
如果面积为负值，是顺时针。

计算的时候要注意，多边形的边界是个环，首尾闭合，最后一点和起点，坐标相同，别少个节点。

2.2 鞋带公式

鞋带公式也叫高斯面积公式，是一种数学算法，可求确定区域的一个简单多边形的面积。

所谓“简单多边形”，可以是凹、或凸多边形，但原则上边与边之间不能有交叉。

鞋带公式如下：

$|\sum^n_{i=1}{(x_i·y_{i+1}-y_i·x_{i+1})}|$

因为判断环的方向只需要知道多边形面积的正负，所以最终使用的“简化版鞋带公式”为：

$\sum^n_{i=1}{(x_i·y_{i+1}-y_i·x_{i+1})}$ 文章来源地址https://www.toymoban.com/news/detail-465055.html

三、代码实现

// 点 对象
struct Vertex{
    Vertex(double px=0.0, double py=0.0) {
        x = px;
        y = py;
    }
    double x;
    double y;
};

// 多边形对象
class Poly
{
public:
	vector<Vertex> vertex; // 顶点集
};

// 判断多边形顺逆时针（true：顺时针，false：逆时针）
bool judgePolyDirection(Poly poly){
	double s = 0;
	for (int i = 0; i < poly.vertex.size(); i++){
		int j = i + 1 < poly.vertex.size() ? i +1:0;
		s += (poly.vertex[i].x * poly.vertex[j].y - poly.vertex[i].y * poly.vertex[j].x);
	}
	return s < 0;
}