二叉树的基本认识（三）-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树的基本认识（三）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

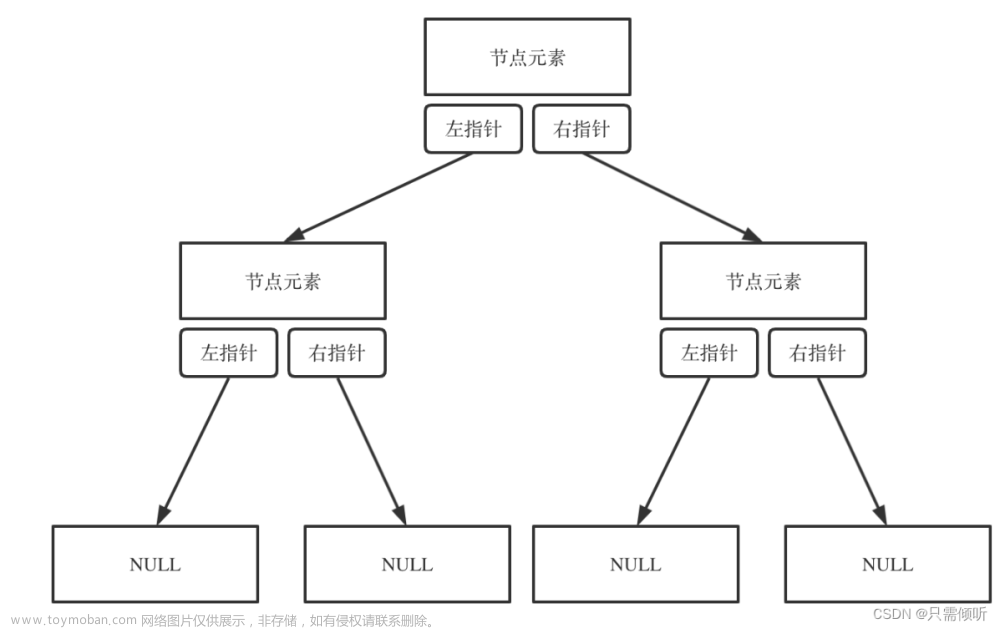
当我们学会遍历后，我们学习二叉树后面的知识就容易多了。如，如何获取二叉树里的数据个数。这简直不要太简单，我们只需遍历一遍就行，不管是前中后，还是层序遍历都可以。这个我就不写了。那么我们如何获取叶子节点的个数（叶子节点就是没有子节点的节点），只要我们了解它的概念，我们就可以判断它的记数条件了，而我们直到它的条件后就可以通过遍历二叉树来计算了。

int getLeafNodeCount2(TreeNode root) {
    if (root == null){
        return 0;
    }
    if (root.left == null && root.right == null){
        return 1;
    }
    return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right);
}

那么我们如果想获取二叉树的高度呢？首先要获取二叉树的高度，我们可以通过拆分二叉树来计算，我们可以将二叉树分为左右子树和根节点，然后比较左右子树的最高的高度来计算，而左右子树又可以去分为左右子树和根节点，直到只有根节点为止。分析完后，我们就可以根据我们的逻辑去写代码了。

int getHeight(TreeNode root) {
    if (root == null){
        return 0;
    }
    int left = getHeight(root.left);
    int right = getHeight(root.right);
    return Math.max(left,right) + 1;
}

那么我想知道在二叉树的某层有多少个节点，那么我应该如何去做呢？同样我们可以去拆分二叉树，将它分为二叉树分为左右子树和根节点，但是我们得判断，如果它在前面就断掉了怎么办，因此我们得将它断掉的结果给考虑到。考虑好后我们就可以将左右子树在该层的的节点相加，而左右子树又可以分为左右子树和根节点，是不是与上面的一样？其实没错，毕竟二叉树本就是递归组成，运用递归来解决问题再合适不过了，而递归在思想上又大同小异，因此当我们学会一个二叉树的解法，就可以触类旁通了。

int getKLevelNodeCount(TreeNode root, int k) {
    if (root == null){
        return 0;
    }
    if (k == 1){
        return 1;
    }
    return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1);
}

而在二叉树中检测某个值是否存在我就不写了，现在我们写一个稍微难一点的，判断二叉树是否为完全二叉树。（全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树），有人或许会问，这是不是又要用递归来写啊？不，这个我们不用递归来写，虽然用不到递归，但是我们要用到队列来写，我们先来分析为什么要用队列，首先我们可以知道，二叉树里不考虑那些奇奇怪怪的分类，就只有两类二叉树，一类普通的，一类完全的，知道后我们就开始谈为什么用队列了。首先我们开始将根节点放入队列里面，然后删除该节点，如果该节点不为null，就将它的左右子节点放入队列，然后再重复上述步骤，删除节点，判断节点是否为null，不是就将它的左右子节点放入队列，不就是一个循环吗？对，没错，那么我们何时应该去结束循环呢？等我们删除的节点为null时，或者该队列为空时结束循环（不过等到该队列为空时，早已经删除到了null了），为什么要这么做呢？其实是如果是完全二叉树的话，那么当我们删除到了null时，这是队列里面所存的一定都是null，如果不是完全二叉树的话，它里面的所存的就不全是null了。如果你们不信的话，可以亲自画图试试。

boolean isCompleteTree(TreeNode root) {
    if (root == null){
        return true;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while(!queue.isEmpty()){
        TreeNode tmp = queue.poll();
        if (tmp != null){
            queue.offer(tmp.left);
            queue.offer(tmp.right);
        }else {
            break;
        }
    }
    while (!queue.isEmpty()){
        if (queue.poll() != null){
            return false;
        }
    }
    return true;
}

到此二叉树的基本认识就已经讲完了，不过肯定会有其他的二叉树的方法没有提到过，不过万变不离其宗，我们也不至于一点方法都没有。文章来源地址https://www.toymoban.com/news/detail-465166.html

到了这里，关于二叉树的基本认识（三）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！