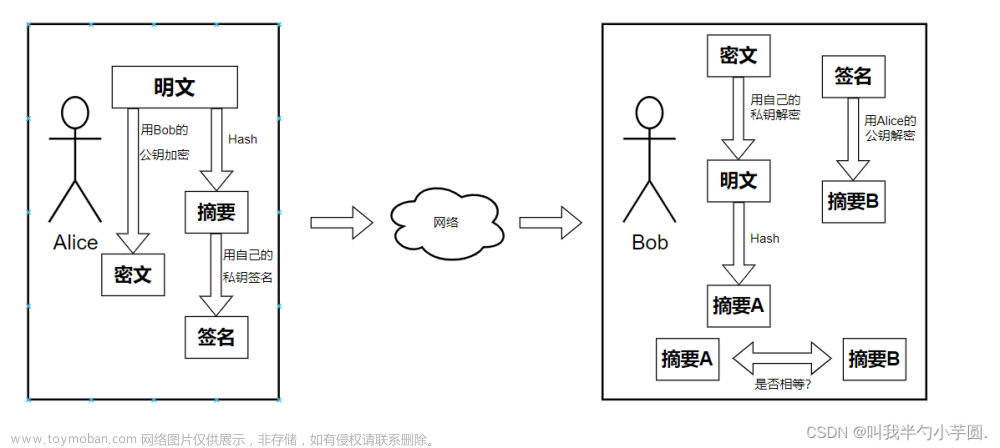
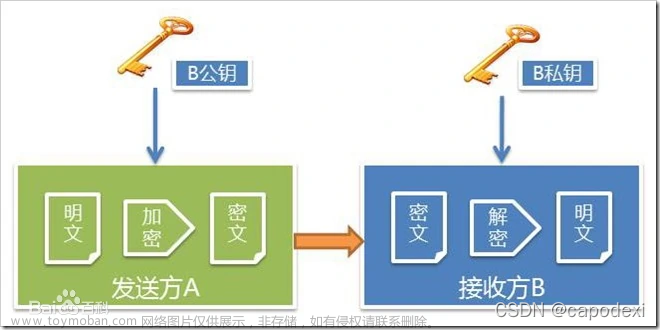
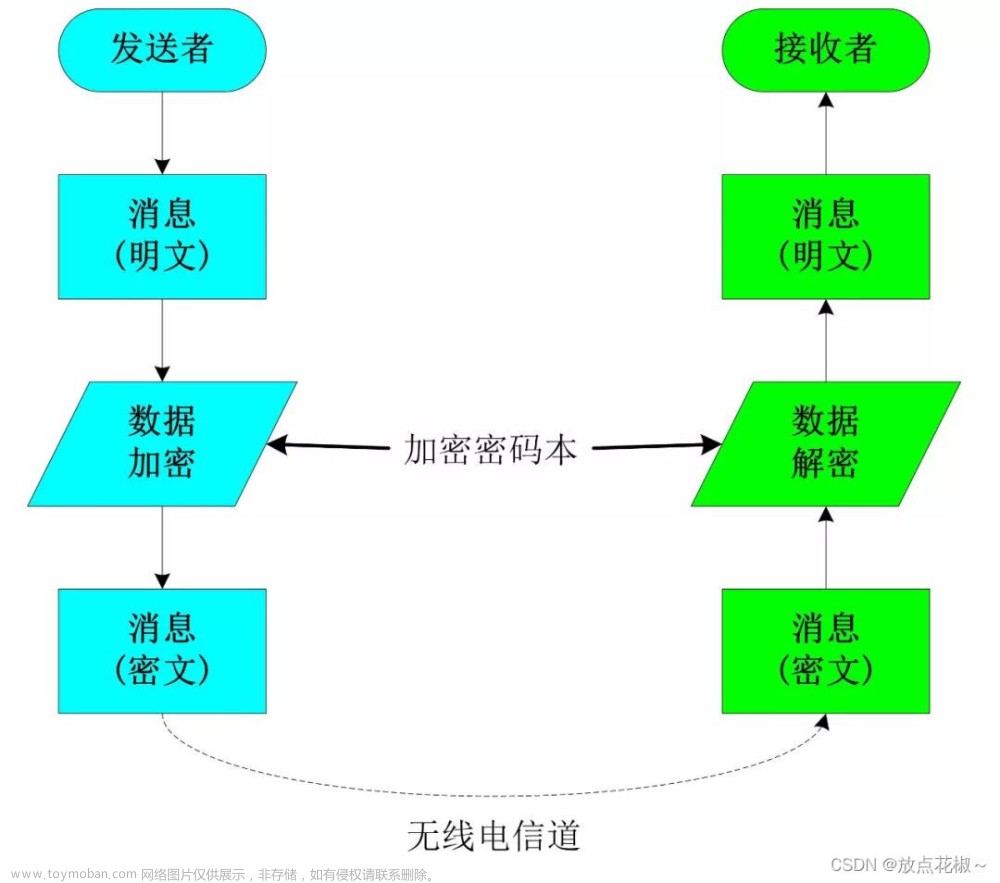
1. 选择明文攻击不可区分性实验
运行生成密钥 ;输出给敌手,敌手可以访问预言机,并输出一对长度相等的消息;选择一个随机比特 ,计算出挑战密文交给 ;敌手继续访问预言机,输出一个比特;如果 ,则,成功。
2. 选择明文攻击条件下的不可区分加密
对称密钥加密方案满足:如果对任意概率多项式敌手,存在可忽略函数,使
则满足选择明文攻击条件下的不可区分加密。
3. 伪随机函数构造安全的构造方法
令是伪随机函数,定义一个消息长度为的对称密钥加密方案如下:
:输入,均匀随机地选择密钥
:输入密钥和消息,均匀随机选择,输出密文
:输入密钥和密文,输出明文
4. 伪随机函数
令是有效的、长度保留的、带密钥的函数。如果对于所有多项式时间的区分器,存在可忽略函数,满足
,
则是一个伪随机函数,其中是随机均匀选择的,是将比特字符串映射到比特字符串的函数集合中均匀随机选择出来的。
5. 选择明文攻击下的不可区分性
如果是伪随机函数,则上述构造方法为消息长度为的定长对称密钥加密方案,在选择明文攻击下不可区分。
书《现代密码学——原理与协议》中针对此类型的归约给出了通用思路:首先在理想的世界中分析方案的安全性,即用真正的随机函数来取代,然后说明此时的安全性;然后当被使用时,如果该方案不是安全的,则意味着将从真正的随机函数中区分出来是可能的。
分别创建两个情景:
- 敌手攻击其对应的挑战者
挑战者有两种方式使用函数来输出:真随机函数和伪随机函数。随机地选择交给敌手来判断该是随机的还是伪随机的。若输出满足,则敌手成功。
如果,则敌手成功的概率为
如果,则敌手成功的概率为
且伪随机函数满足
图解:

- 敌手攻击
生成两个长度相等的字符串和。随机选择,计算密文交给来判断来自还是。若输出,则成功。
如果来自随机函数,令加密方案:用真正的随机函数来代替伪随机函数,其他与相同。每个敌手最多向它的加密预言机问询多项式次,有
下面证明此命题:
令表示生成挑战密文时生成的随机字符串。有两种情况:
值被加密预言机使用来回答至少一个的问询:
无论何时加密预言机返回一个密文来回应加密消息的请求,敌手由掌握了值。此时,可能轻易地判断出哪一个消息被加密。因为最多向预言机问询次,并且每次预言机回答它的问询都是使用一个均匀选择的,所以该事件发生的概率最多为。
值没有被加密预言机用来回答的问询:
这种情况下,在和加密预言机的交互过程中,没有掌握任何关于值的信息。在这种情况下,输出的概率刚好是(类似于“一次一密”)。
令表示值被加密预言机使用来回答至少一个的问询的事件。则有
得证。
如果来自伪随机函数,则敌手成功的概率被表示为
如果下面不等式成立,就可以说明加密协议是安全的:
图解:

证明:根据上面所述的情景,正式说明逻辑命题等价式表示为:
令区分器使用作为子程序,来模拟不可区分实验。

如果的预言机是一个伪随机函数,那么当被作为一个子程序运行时的所见视图分布,与在实验中所见的视图分布是相同的。则
如果的预言机是一个随机函数,那么当被作为一个子程序运行时的所见视图分布,与在实验中所见的视图分布是相同的。则
根据不等式有
相关于
由于满足多项式,得证。文章来源:https://www.toymoban.com/news/detail-465376.html
6. 参考文献
乔纳森.卡茨,耶胡达.林德尔著,任伟译,现代密码学——原理与协议,国防工业出版社,2017年第一版第4次印刷.文章来源地址https://www.toymoban.com/news/detail-465376.html
到了这里,关于密码学归约证明——选择明文攻击下的不可区分性的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!