目录
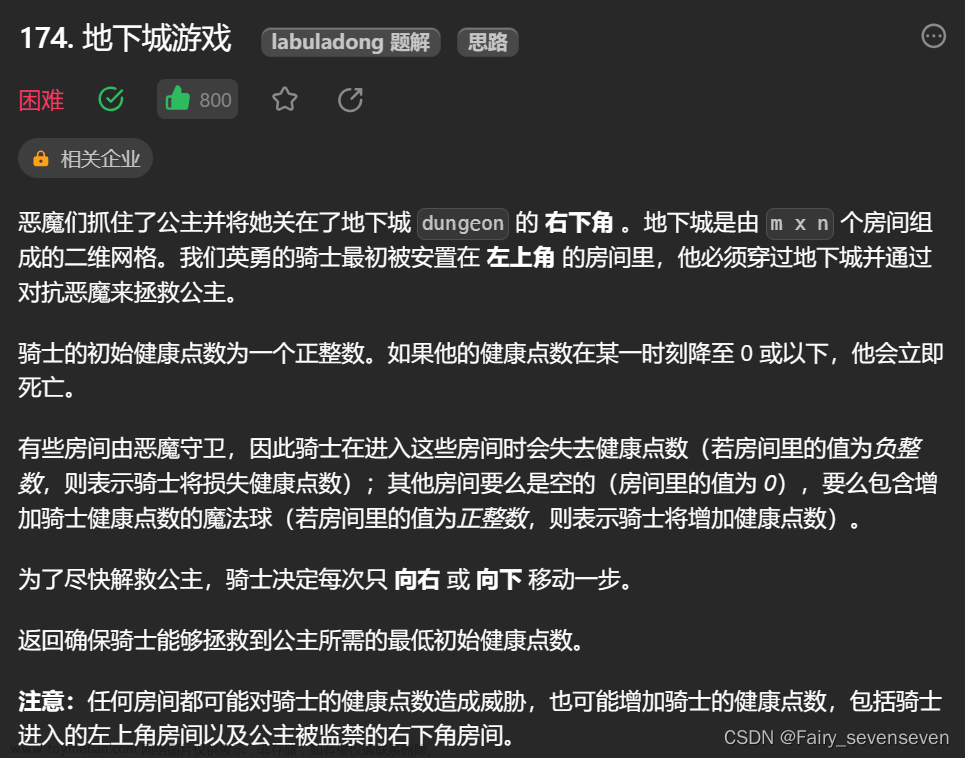
1.题目概述：
2.题目解析：
3.题目代码：
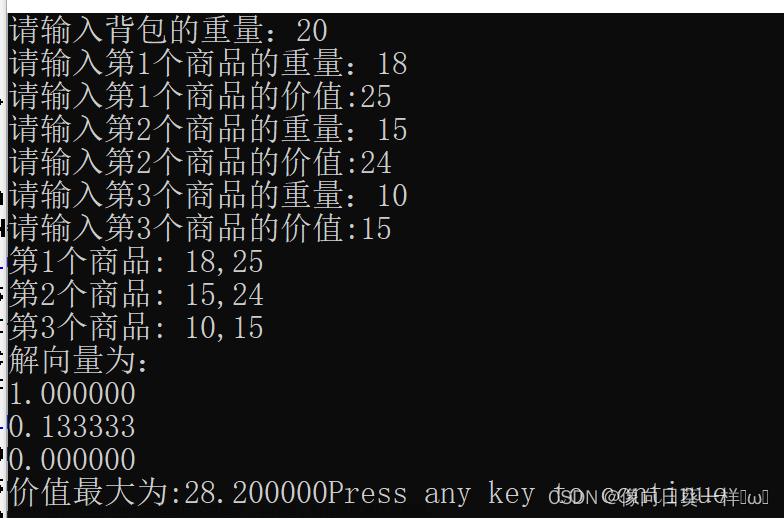
4.样例展示：
5.题目总结：
1.题目概述：
某实验室经常有活动需要叫外卖，但是每次叫外卖报销的经费总额最大为C元，有N种菜可以点，经过长时间的点菜，实验室对每种菜i都有一个量化的评分Vi，这种菜的价格为Pi，问如何选择各种菜（每种菜只能点一次），才能在报销额度范围内使点到菜的总评价分数最高。
2.题目解析：
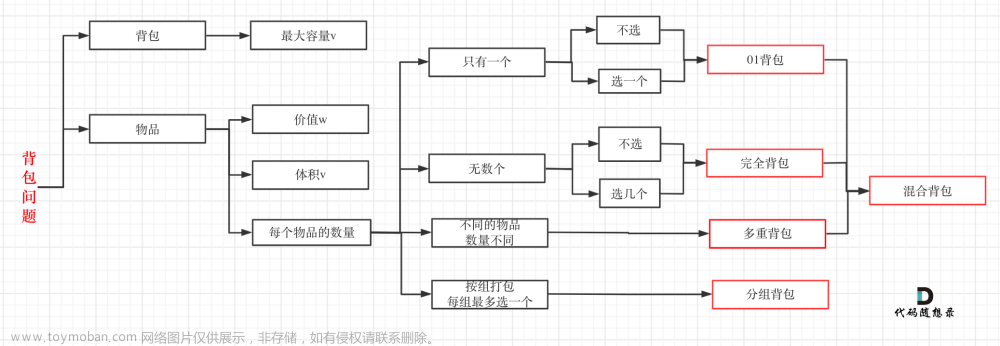
类似0/1背包，每个菜只能选或不选，且最多只能选一次
用dp[i][j]表示前i个菜金额为j时的最大评分，则dp[C][j]即为答案，初始化全0由于每种菜最多只能选一次，为了避免重复计算某道菜，要在外层循环菜品
对应每种菜品，不选时，dp[j]不变
如果要选择，在金额 j 时，比较更新加入后的dp[j]
如果加入比原来评分高，那就加入并更新，否则就不加入保持原状
故得转移方程dp[i][j] = max( dp[i-1][j] , dp[i-1][j-p[i]] + v[i])
由于每个菜品只循环了一次，所以不会重复
对每种菜品，在每个符合条件的价格处选择是否加入，所以每个价格处都是当前最优解，循环完就是全局最优解.
类似0/1背包问题，通过表格可以更能清晰的表达：
3.题目代码：
#include <stdio.h>
#include <math.h>
int max(int a, int b)
{
if (a > b)
return a;
else
return b;
}
int main()
{
int n, C, i, j, k = 0;
int temp;
printf("请输入菜的种类个数:");
scanf("%d", &n);
printf("请输入外卖报销最大的经费数额:");
scanf("%d", &C);
int Vi[n], Pi[n], MaxValue[C + 1][n + 1], a[n];
printf("请输入每种菜的量化评分:");
for (i = 0; i < n; i++)
scanf("%d", &Vi[i]);
printf("请输入与之对应的每种菜的价格:");
for (i = 0; i < n; i++)
scanf("%d", &Pi[i]);
for (i = 0; i < C + 1; i++)
MaxValue[i][0] = 0;
for (i = 0; i < n + 1; i++)
MaxValue[0][i] = 0;
for (j = 1; j <= n; j++)
{
for (i = 1; i <= C; i++)
{
if (Pi[j - 1] > i)
MaxValue[i][j] = MaxValue[j - 1][i];
else
MaxValue[i][j] = max(MaxValue[i - Pi[j - 1]][j - 1] + Vi[j - 1], MaxValue[i][j - 1]);
}
if (MaxValue[i - 1][j] != MaxValue[i - 1][j - 1])
{
a[k] = j;
k++;
}
}
printf("选择的菜的种类为: ");
for (i = 0; i < k; i++)
{
printf("第%d种 ", a[i]);
}
printf("\n");
printf("点到菜的总评价分数为: %d\n", MaxValue[C][n]);
return 0;
}4.样例展示：
文章来源：https://www.toymoban.com/news/detail-465468.html
5.题目总结：
此次实验重难点在于动态规划递归式的求解，以及动态规划表的构造。同时，二维数组的定义，应用和传值，我认为也是这次实验的一大难点。总结来说，在算法问题的设计上，采用递归式，构建动态规划表，不断的得到最优值是问题的关键。这是对该问题的简要分析。文章来源地址https://www.toymoban.com/news/detail-465468.html
到了这里，关于点菜问题：动态规划（C语言实现）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
