实验目的
1. 掌握顺序查找技术和拆半查找技术以及部分排序算法的设计思想;
2. 掌握查找、部分排序算法的实现与执行过程。
实验原理
查找算法
1.顺序查找:从数组第一个元素开始逐个比较,找到后返回相应下标。
2.折半查找:从数组中间开始比较,如果需查找值比中间值大,则在中间值右边继续找,重复上述步骤,直至找到该元素;如果需查找值比中间值小,则在中间值左边继续找,重复上述步骤。
3. 二叉查找树:先利用递归方式构建一棵二叉查找树,使得左子树所有结点都比根节点小,右子树所有结点都比根节点大。查找时,通过与根节点比较大小即可分别对应进入左右子树,依次递归,直至找到该元素。
排序算法
1. 直接插入排序:假设把数组分为两部分,一部分是初始时是R1[1],另一部分是R2[2……n-1],每次将R2的第一个元素抽出来与R1中的数进行比较,找到合适的位置插入,然后把这个元素加入R1,依次循环直到R2的数组为空。
2. 折半插入排序:与直接插入类似,只不过在寻找插入位置时采用了折半方法。
3. 希尔排序:设置初始增量为n/2(n为数组长度),将数组划分为n/2个小数组,然后对每个小数组进行直接插入排序,一轮结束后,再将增量/2,重复上述步骤,直至增量=0,即排序完成。
4. 冒泡排序:设置双重循环,相邻元素之间比较大小根据大小进行移动。并添加标志,如果剩下的序列中没有元素发生移动,则表明数组元素已排序完成,可以提前退出。
5. 快速排序:初始时,将数组的第一个元素作为标记,然后扫描数组,将比标记小的数移到标记左边,比数组大的数移到标记右边,最后返回标记的位置;所以以标记为中心,数组被划分为了两部分,假设为左右子表,接着对左右子表用递归方式重复上述步骤即可完成排序。
6. 选择排序:设置双重循环,初始时假设第一个元素是最小值,向后扫描找是否有比第一个更小的元素,如果有则记录它的下标,直到找到真正的最小值,然后把最小值和第一个元素交换位置;第二趟排序则设第二个元素是最小值,重复上述步骤,即可完成排序。
7. 堆排序:将数组看作是一棵完全二叉树的顺序存储结构。初始时,需要构建大根堆。由完全二叉树性质可得,序号大于n/2的结点都是叶子结点,叶子结点满足堆,所以只需要对序号小于n/2的这部分结点进行筛选调整。之后再反复重建堆即可完成排序。
8. 归并排序:初始时,设数组分为n个 部分,所以每个部分都是有序的;每一趟排序将两两小数组合并(合并时要比较大小进行排序);最后合并得到一个数组即为有序数组,完成排序。
实验源码
查找
顺序表查找
int SeqSearch(int arr[], int n, int x){//顺序表查找
cout<<endl;
cout<<"-----顺序表查找-----"<<endl;
for (int i=1; i <=n; ++i)
{
if (arr[i] == x)//找到该元素,返回下标
return i;//设数组元素位置从1开始
}
return -1;//若没找到则返回-1
}二分查找
int BinSearch(int arr[], int n, int x){//折半查找
cout<<endl;
cout<<"-----折半查找-----"<<endl;
int low = 1, high = n , mid;
while (low <= high)
{
mid = (low + high) / 2;
if (arr[mid] == x)
return mid;
else if (arr[mid] > x) //如果比中间值小,则在中间值左边查找
high = mid - 1; //更新high
else //如果比中间值大,则在中间值右边查找
low = mid + 1; //更新low
}
return -1;//若没找到则返回-1
}二叉树查找
//定义二叉树的结构
typedef char ElemType;
typedef struct BiTNode{
ElemType data; //数据域
struct BiTNode* lchild, * rchild; //左右子树
} BiTNode, *BiTree; //结点、整颗树
//在二叉查找树中插入新结点
bool InsertBST(BiTree& bt, char ch){
if (bt == NULL) { //创建新结点
bt = new BiTNode;
bt->data = ch;
bt->lchild = bt->rchild = NULL;
return true;
}
else if (bt->data == ch){
cout << "已存在该元素,请重新输入!" << endl;
return false;
}
else if (ch < bt->data)
return InsertBST(bt->lchild, ch);
else
return InsertBST(bt->rchild, ch);
}
//创建二叉树
BiTree CreateBST(BiTree& bt){
bt = NULL;
char ch;
for (int i = 0; i < 10; ++i){
cout << "请输入第" << i + 1 << "个字母: ";
cin >> ch;
if (!InsertBST(bt, ch))//如果输入的数据重复,--i使得可以重新输出第i个字母;不重复则正常插入
--i;
}
cout << endl;
return bt;
}
//二叉排序树的查找
BiTree SearchBST(BiTree bt, char ch){
if (bt == NULL || bt->data == ch){
cout<<"查找成功"<<endl;
return bt;
}
if (ch < bt->data) //ch比根节点值小
return SearchBST(bt->lchild, ch);
else //ch比根节点大
return SearchBST(bt->rchild, ch);
}排序
直接插入排序
int process=1;
void InsertSort(int arr[], int n){ //直接插入排序
cout<<endl;
cout<<"------直接插入排序------"<<endl;
int i, j;
process = 1; //趟数
for (i = 2; i <=n; ++i){
if (arr[i] < arr[i - 1]){
arr[0] = arr[i]; //将待插入的记录暂存到监视哨a[0]中
arr[i] = arr[i - 1]; //arr[i-1]后移
for (j = i - 2; arr[0] < arr[j]; --j) { //从后向前寻找插入位置,逐个后移,空出插入位置
arr[j + 1] = arr[j];
}
arr[j + 1] = arr[0]; //插入
}
cout << "第" << process++ << "次排序: ";
printArr(arr,n); //输出序列
cout << endl;
}
}折半排序
void BInsertSort(int arr[],int n){ //折半插入排序
cout<<endl;
cout<<"-----折半插入排序-----"<<endl;
int i, j, low, high, m;
process = 1; //趟数
for (i = 2; i <=n; ++i){
if (arr[i] < arr[i - 1]){
arr[0] = arr[i]; //将待插入的记录暂存到监视哨中
low = 1; high = i; //置查找区间初值
while (low <= high){ //在arr[low..high]中折半查找插入的位置
m = (low + high) / 2; //折半
if (arr[0] < arr[m]) //插入点在前一子表
high = m - 1;
else //插入点在后一子表
low = m + 1;
}
for (j = i - 1; j >= high + 1; --j){ //后移
arr[j + 1] = arr[j];
}
arr[high + 1] = arr[0]; //将arr[0]即原arr[i],插入到正确位置
}
cout << "第" << process++ << "次排序: ";
printArr(arr,n); //输出数组元素
cout << endl;
}
}希尔排序
void ShellSort(int arr[], int n){ //希尔排序
cout<<endl;
cout<<"-----希尔排序-----"<<endl;
int i, j, d;
d = n / 2; //增量初始值
process = 1; //趟数
while (d > 0){ //当增量d=0时,则排序结束
for (i = d+1; i <= n; ++i){ //对所有组进行直接插入排序
if (arr[i] < arr[i - d]){
arr[0] = arr[i]; //将待插入的记录暂存到监视哨中
for (j=i-d; (arr[0] < arr[j]) && (j>0) ; j = j - d){ //从后向前寻找插入位置,逐个后移,空出插入位置
arr[j + d] = arr[j];
}
arr[j + d] = arr[0]; //插入正确位置
}
}
d = d / 2; //减小增量
cout << "第" << process++ << "次排序: ";
printArr(arr,n); //输出序列
cout << endl;
}
}冒泡排序
void BubbleSort(int arr[],int n){ //冒泡排序
cout<<endl;
cout<<"-----冒泡排序-----"<<endl;
int j,m, flag;
m = n - 1;
flag = 1; //flag用来标记某一趟排序是否发生交换
process = 1; //趟数
while(m && flag){
flag = 0; //flag置为0,如果本趟排序没有发生交换,则不会执行下一趟排序
for (j = 1; j <= m; ++j){
if (arr[j] > arr[j + 1]){
flag = 1; //flag置为1,表示本趟排序发生了交换
arr[0] = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = arr[0]; //交换前后两个记录
}
}
--m;
if (flag == 0) return; //没有排序,说明排完了,直接跳出
else{
cout << "第" << process++ << "次排序: ";
printArr(arr,n);
cout << endl;
}
}
}快速排序
int Partition(int arr[], int low, int high){ //划分
//对arr中的子表arr[low..high]进行一趟排序,返回枢轴位置
arr[0] = arr[low]; //用子表的第一个记录做标记
while (low < high){ //从序列的两端交替地向中间扫描
while (low < high && arr[high] >= arr[0]){
--high;
}
arr[low] = arr[high]; //将比标记记录小的记录移到左边
while (low < high && arr[low] <= arr[0]){
++low;
}
arr[high] = arr[low]; //将比标记记录大的记录移到右边
}
arr[low] = arr[0]; //标记记录到位
cout << "第" << process++ << "次排序: ";
printArr(arr,10);
cout << endl;
return low; //返回标记位置
}
void QuickSort(int arr[], int low, int high){ //快速排序
int i;
if (low < high){
i = Partition(arr, low, high); //将arr[low..high]一分为二,i是标记位置
QuickSort(arr, low, i - 1); //对左子表递归排序
QuickSort(arr, i + 1, high); //对右子表递归排序
}
}简单选择排序
void SelectSort(int arr[],int n){ //简单选择排序
cout<<endl;
cout<<"-----选择排序-----"<<endl;
int i, j, temp; //假设arr[temp]为最小
process = 1; //趟数
for (i = 1; i <n-1; ++i){ //在arr[] 中选择关键字最小的记录
temp = i;
for (j = i + 1; j <=n; ++j){
if (arr[j] < arr[temp])
temp = j; //temp指向此趟排序中关键字最小的记录
}
if (temp != i){ //交换r[i]与r[k]
arr[0] = arr[i];
arr[i] = arr[temp];
arr[temp] = arr[0];
}
cout << "第" << process++ << "次排序: ";
printArr(arr,n);
cout << endl;
}
}
vo堆排序
void sift(int arr[], int low, int high){ //筛选
int i = low, j = 2 * i; //根据完全二叉树性质,i的孩子为2*i和2*i+1
arr[0] = arr[i];
while (j <= high){
if (j < high && arr[j] < arr[j + 1]) //若右孩子大
++j;
if (arr[0] < arr[j]){ //将arr[j]调整到双亲结点位置上
arr[i] = arr[j];
i = j; //修改i和j,以便向下筛选
j = 2 * i;
}else{
break;
}
}
arr[i] = arr[0]; //被筛选结点放入最终位置上
}
void HeapSort(int arr[], int n){ //堆排序
cout<<endl;
cout<<"-----堆排序-----"<<endl;
int i;
process = 1; //趟数
for (i = n / 2; i >= 1; --i) //建立初始堆,调用sift算法(n/2)(向下取整)次
sift(arr, i, n);
for (i = n; i >= 2; i--){
//a[0]为哨兵位
arr[0] = arr[i]; //将堆顶元素a[1]和当前未经排序子序列arr[1...i]的最后一个元素交换
arr[i] = arr[1];
arr[1] = arr[0];
sift(arr, 1, i - 1); //重新调整arr[1...i-1]为根堆
cout << "第" << process++ << "次排序: ";
printArr(arr,n);
cout << endl;
}
}归并排序
void Merge(int arr[], int temp[], int low,int mid, int high){ //合并
int i = low,j=mid+1,k=low;
while (i <= mid && j <= high) //将arr中的记录从小到达放入temp中
{
if (arr[i] <= arr[j]){
temp[k++] = arr[i++];
}
else{
temp[k++] = arr[j++];
}
}
while (i <= mid) //若arr[j……high]已遍历完,则将arr[i,mid]复制到temp中
{
temp[k++] = arr[i++];
}
while (j <= high) //若arr[i,mid]已遍历完,则将arr[j……high]复制到temp中
{
temp[k++] = arr[j++];
}
}
void MergeSort(int arr[], int temp[], int low, int high){ //二分归并排序
int s[20];
if (low == high)
temp[low] = arr[low];
else{
int mid = (low + high) / 2; //将当前序列一分为二
MergeSort(arr, s, low, mid); //对分裂点的左边序列递归归并排序,结果放入S[low……mid]
MergeSort(arr, s, mid + 1, high); //对分裂点的右边序列递归归并排序,结果放入S[mid+1……high]
Merge(s, temp, low, mid, high); //合并S[low……mid]和S[mid+1……high]
cout << "第" << process++ << "次排序的中间过程: ";
printArr(temp,20);
cout << endl;
}
}
main
int main(){
// cout<<"初始序列: ";
// for(int i=1;i<=10;i++){
// cin>>arr[i];
// }
//排序
// InsertSort(arr,10);
// BInsertSort(arr,10);
// ShellSort(arr,10);
// BubbleSort(arr,10);
// cout<<endl;
// QuickSort(arr,0,10);
// SelectSort(arr,10);
// HeapSort(arr,10);
//查找
// cin>>x;
// cout<<SeqSearch(arr,10,x);
// cout<<BinSearch(arr,10,x);
// BiTree Tree=NULL;
// CreateBST(Tree);
// cout<<"输入要查的值:";
// char x;
// cin>>x;
// SearchBST(Tree,x);
return 0;
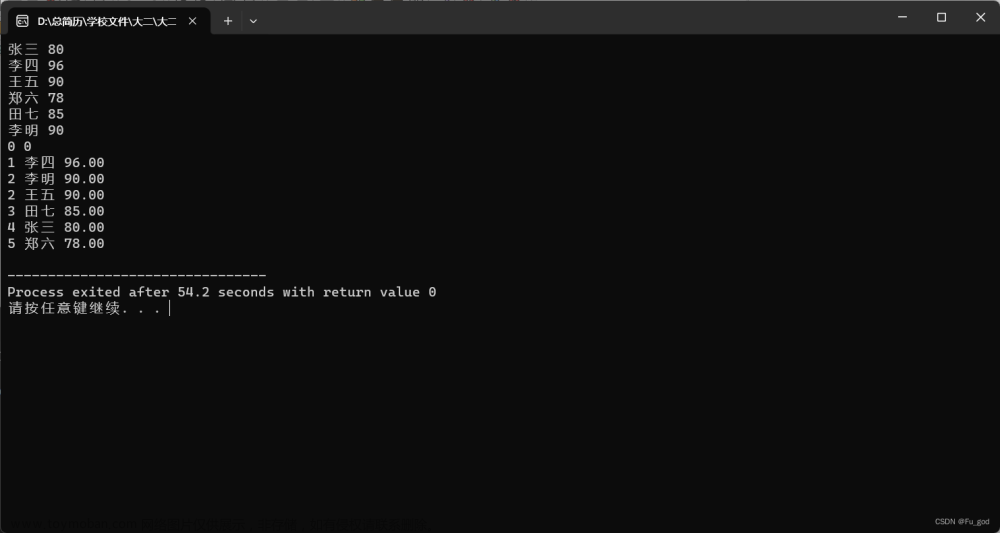
}实验结果
查找



排序



等等等等(篇幅有限)
实验心得
-
对于序列,一般从索引1开始存放数据,索引0留着,可作为哨兵位,因此一些for循环中的结束条件是i<n还是i<=n要考虑清除。实验中设置长度为11的数组,首位放0。实际排序是后面10个数字。

2.查找过程中,二分查找针对有序序列,因此要先对序列排序,再二分查找,一开始疏忽了这个点,出了小错误,自己手画一遍查找流程才恍然大悟。
3.直接插入排序、冒泡排序、简单选择排序相对比较慢,但是代码比较简单;快速排序、堆排序、归并排序比较快,但代码相对复杂。
今日创作在听《龙卷风》
其他博文:文章来源:https://www.toymoban.com/news/detail-465599.html
数据结构实验报告(一)——线性表、堆栈和队列的操作与实现_队列的基本操作实验报告-CSDN博客https://blog.csdn.net/luohaojia123/article/details/128689896?spm=1001.2014.3001.5501数据结构实验报告(二)——二叉树基本操作_数据结构实验报告二叉树的基本操作-CSDN博客https://blog.csdn.net/luohaojia123/article/details/127905639?spm=1001.2014.3001.5502数据结构实验报告(三)——图的操作和实现_图的基本操作数据结构实验总结与体会(问题及解决方案、收获与感想等,不低于500字)-CSDN博客https://blog.csdn.net/luohaojia123/article/details/128690098?spm=1001.2014.3001.5501文章来源地址https://www.toymoban.com/news/detail-465599.html
到了这里,关于数据结构实验报告(四)——查找和排序算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!