一、二次曲线与对偶二次曲线
最近在看基于椭球体的物体SLAM过程中,经常涉及到椭球体的空间几何知识,这里先补充一下一些空间几何相关的基础,参考链接。
椭球体本身属于二次曲面的一种,二次曲面是对空间形状的描述,属于3d的内容,与之对应的2d描述是二次曲线,这里我们先从二次曲线开始,二次曲线简单来说就是高考题倒数第二题的考试内容,包括椭圆、双曲线和抛物线三种,这三种曲线来自于用一个平面切割二次曲面,最多可以得到三种曲线,即三种二次曲线。
对于一条二次曲线,我们可以使用代数形式对其进行描述:
这里的xy本身对应的是一个二次曲线上的坐标(x,y),当我们把坐标换为齐次坐标时,可以得到齐次坐标下的二次曲线表达式:
将该式子整理为矩阵形式可得:
由于该式子的右侧为0,因此我们可以对式子左右两侧同时除以一个常数,这里我们选择同时除以f,那么二次曲线的参数矩阵Q中的六个未知数就变成了五个,相当于我们不考虑二次曲线的尺度,让自由度减少一个变成了五个,也就是说对于任何一条二次曲线,我们可以用曲线上的五个点来解出矩阵Q,从而表示这个二次曲线。
由于我们对点的坐标使用的是向量的形式,我们也可以将其换为一条线的向量表示,形式上没有发生变化但是几何意义发生了变化。对于任何一条二次曲线,其切线可以表示为:
这里切线可以证明,主要是证明点x同时落在二次曲线和直线上,且直线和二次曲线相交与唯一一点,这里就不展开详细算了。有了切线的表示方式,那么我们可以用切线来表示切点x,将点x带入二次曲线的表达式,就可以得到用切线来表示的二次曲线:

为了式子的简介,这里我们将矩阵C的逆矩阵另作定义:
这时我们就得到了用切线表示的二次曲线,这种用切线表示的方式我们称为对偶二次曲线,也就是说二次曲线和对偶二次曲线本质上都是对二次曲线的形容,只不过表示方式不一样,用点来表示的称为二次曲线,而用切线表示的称为对偶二次曲线,切线会与二次曲线产生交点,两种表示方式正是通过相切来进行的联系。
二、二次曲面与对偶二次曲面
根据前面的推理,我们可以直接将二次曲线扩展到二次曲面上,对于任何一个二次曲面,我们都可以用代数形式对其进行描述,将代数形式中的坐标替换为齐次坐标后整理为矩阵形式,可以得到二次曲面的矩阵Q,两侧同时除以常数消除尺度同时减少一个自由度,对向量进行替换变成切面形式,切面进行整理并带入二次曲面表达式最终得到对偶二次曲面。 文章来源:https://www.toymoban.com/news/detail-465701.html
文章来源:https://www.toymoban.com/news/detail-465701.html
三、总结
无论是二次曲线还是二次曲面,带与不带对偶,区别就在于是否使用切线/面来对其进行描述,本质上说的还是同一个东西,在论文中使用的主要是二次曲面中的椭球ellipsoid,使用这一形式进行描述主要是在投影过程中的描述性更好,不会出现空间立方体那样不规则的投影结果,但是缺点在于椭球的自由度有八个,需要至少八个约束才能描述一个椭球,这更需要对空间物体的性质进行更加细致的研究。文章来源地址https://www.toymoban.com/news/detail-465701.html
到了这里,关于【学习记录】二次曲线、二次曲面、对偶二次曲线、对偶二次曲面的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!








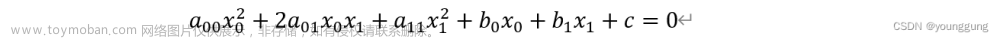
![[足式机器人]Part3机构运动微分几何学分析与综合Ch03-1 空间约束曲线与约束曲面微分几何学——【读书笔记】](https://imgs.yssmx.com/Uploads/2024/02/677088-1.png)



