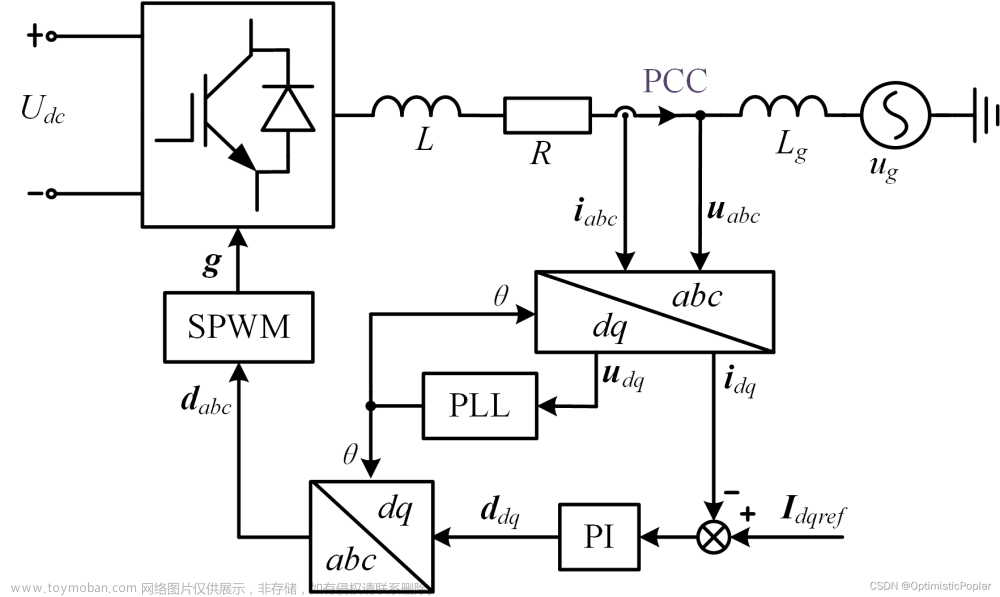
我们在用matlab的dq变换模块的时候,发现dq变换模块有两种变换方式:

选择Aligned with phase A axis还是90 degree behind phase A axis?
通过查阅Matlab的官方的介绍:
派克变换模块的介绍:abc to dq0, dq0 to abc
abc 到 dq0 模块使用 Park 变换将三相 (abc) 信号变换为 dq0 旋转参考系。旋转框架的角位置由输入 wt 给出,以 rad 为单位。
dq0 到 abc 模块使用逆帕克变换将 dq0 旋转参考系变换为三相 (abc) 信号。旋转框架的角位置由输入 wt 给出,以 rad 为单位。
该块支持用于 Park 转换的两种约定:
当旋转坐标系在 t = 0 时与 A 相轴对齐时,即在 t = 0 时,d 轴与 a 轴对齐。这种类型的 Park 变换也称为基于余弦的 Park 变换。
当旋转框架在相位 A 轴后 90 度对齐时,即在 t = 0 时,q 轴与 a 轴对齐。这种类型的 Park 变换也称为基于正弦的 Park 变换。在具有三相同步和异步电机的 Simscape™ Electrical™ 专用电力系统模型中使用此转换。
Aligned with phase A axis
中国的课本一般用的是这个公式
- 派克正变换(基于余弦)
[ u d u q u 0 ] = 2 3 [ cos ( ω t ) cos ( ω t − 2 π 3 ) cos ( ω t + 2 π 3 ) − sin ( ω t ) − sin ( ω t − 2 π 3 ) − sin ( ω t + 2 π 3 ) 1 2 1 2 1 2 ] [ u a u b u c ] \left[\begin{array}{l} u_d \\ u_q \\ u_0 \end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc} \cos (\omega t) & \cos \left(\omega t-\frac{2 \pi}{3}\right) & \cos \left(\omega t+\frac{2 \pi}{3}\right) \\ -\sin (\omega t) & -\sin \left(\omega t-\frac{2 \pi}{3}\right) & -\sin \left(\omega t+\frac{2 \pi}{3}\right) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{array}\right]\left[\begin{array}{l} u_a \\ u_b \\ u_c \end{array}\right] ⎣ ⎡uduqu0⎦ ⎤=32⎣ ⎡cos(ωt)−sin(ωt)21cos(ωt−32π)−sin(ωt−32π)21cos(ωt+32π)−sin(ωt+32π)21⎦ ⎤⎣ ⎡uaubuc⎦ ⎤
$$
\left[\begin{array}{l}
u_d \\
u_q \\
u_0
\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}
\cos (\omega t) & \cos \left(\omega t-\frac{2 \pi}{3}\right) & \cos \left(\omega t+\frac{2 \pi}{3}\right) \\
-\sin (\omega t) & -\sin \left(\omega t-\frac{2 \pi}{3}\right) & -\sin \left(\omega t+\frac{2 \pi}{3}\right) \\
\frac{1}{2} & \frac{1}{2} & \frac{1}{2}
\end{array}\right]\left[\begin{array}{l}
u_a \\
u_b \\
u_c
\end{array}\right]
$$
- 派克逆变换(基于余弦)
[ u a u b u c ] = [ cos ( ω t ) − sin ( ω t ) 1 cos ( ω t − 2 π 3 ) − sin ( ω t − 2 π 3 ) 1 cos ( ω t + 2 π 3 ) − sin ( ω t + 2 π 3 ) 1 ] [ u d u q u 0 ] \left[\begin{array}{l} u_a \\ u_b \\ u_c \end{array}\right]=\left[\begin{array}{ccc} \cos (\omega t) & -\sin (\omega t) & 1 \\ \cos \left(\omega t-\frac{2 \pi}{3}\right) & -\sin \left(\omega t-\frac{2 \pi}{3}\right) & 1 \\ \cos \left(\omega t+\frac{2 \pi}{3}\right) & -\sin \left(\omega t+\frac{2 \pi}{3}\right) & 1 \end{array}\right]\left[\begin{array}{l} u_d \\ u_q \\ u_0 \end{array}\right] ⎣ ⎡uaubuc⎦ ⎤=⎣ ⎡cos(ωt)cos(ωt−32π)cos(ωt+32π)−sin(ωt)−sin(ωt−32π)−sin(ωt+32π)111⎦ ⎤⎣ ⎡uduqu0⎦ ⎤
$$
\left[\begin{array}{l}
u_a \\
u_b \\
u_c
\end{array}\right]=\left[\begin{array}{ccc}
\cos (\omega t) & -\sin (\omega t) & 1 \\
\cos \left(\omega t-\frac{2 \pi}{3}\right) & -\sin \left(\omega t-\frac{2 \pi}{3}\right) & 1 \\
\cos \left(\omega t+\frac{2 \pi}{3}\right) & -\sin \left(\omega t+\frac{2 \pi}{3}\right) & 1
\end{array}\right]\left[\begin{array}{l}
u_d \\
u_q \\
u_0
\end{array}\right]
$$
90 degree behind phase A axis
当 wt=0 处的旋转坐标系对齐在相位 A 轴后 90 度时,Mag=1 和 Phase=0 度的正序信号产生以下 dq 值:d=1,q=0。
此时的公式为
- 派克正变换(基于正弦)
[ u d u q u 0 ] = 2 3 [ sin ( ω t ) sin ( ω t − 2 π 3 ) sin ( ω t + 2 π 3 ) cos ( ω t ) cos ( ω t − 2 π 3 ) cos ( ω t + 2 π 3 ) 1 2 1 2 1 2 ] [ u a u b u c ] \left[\begin{array}{l} u_d \\ u_q \\ u_0 \end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc} \sin (\omega t) & \sin \left(\omega t-\frac{2 \pi}{3}\right) & \sin \left(\omega t+\frac{2 \pi}{3}\right) \\ \cos (\omega t) & \cos \left(\omega t-\frac{2 \pi}{3}\right) & \cos \left(\omega t+\frac{2 \pi}{3}\right) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{array}\right]\left[\begin{array}{l} u_a \\ u_b \\ u_c \end{array}\right] ⎣ ⎡uduqu0⎦ ⎤=32⎣ ⎡sin(ωt)cos(ωt)21sin(ωt−32π)cos(ωt−32π)21sin(ωt+32π)cos(ωt+32π)21⎦ ⎤⎣ ⎡uaubuc⎦ ⎤
\left[\begin{array}{l}
u_d \\
u_q \\
u_0
\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}
\sin (\omega t) & \sin \left(\omega t-\frac{2 \pi}{3}\right) & \sin \left(\omega t+\frac{2 \pi}{3}\right) \\
\cos (\omega t) & \cos \left(\omega t-\frac{2 \pi}{3}\right) & \cos \left(\omega t+\frac{2 \pi}{3}\right) \\
\frac{1}{2} & \frac{1}{2} & \frac{1}{2}
\end{array}\right]\left[\begin{array}{l}
u_a \\
u_b \\
u_c
\end{array}\right]
- 派克逆变换(基于正弦)
[ u a u b u c ] = [ sin ( ω t ) cos ( ω t ) 1 sin ( ω t − 2 π 3 ) cos ( ω t − 2 π 3 ) 1 sin ( ω t + 2 π 3 ) cos ( ω t + 2 π 3 ) 1 ] [ u d u q u 0 ] \left[\begin{array}{l} u_a \\ u_b \\ u_c \end{array}\right]=\left[\begin{array}{ccc} \sin (\omega t) & \cos (\omega t) & 1 \\ \sin \left(\omega t-\frac{2 \pi}{3}\right) & \cos \left(\omega t-\frac{2 \pi}{3}\right) & 1 \\ \sin \left(\omega t+\frac{2 \pi}{3}\right) & \cos \left(\omega t+\frac{2 \pi}{3}\right) & 1 \end{array}\right]\left[\begin{array}{c} u_d \\ u_q \\ u_0 \end{array}\right] ⎣ ⎡uaubuc⎦ ⎤=⎣ ⎡sin(ωt)sin(ωt−32π)sin(ωt+32π)cos(ωt)cos(ωt−32π)cos(ωt+32π)111⎦ ⎤⎣ ⎡uduqu0⎦ ⎤文章来源:https://www.toymoban.com/news/detail-465840.html
$$
\left[\begin{array}{l}
u_a \\
u_b \\
u_c
\end{array}\right]=\left[\begin{array}{ccc}
\sin (\omega t) & \cos (\omega t) & 1 \\
\sin \left(\omega t-\frac{2 \pi}{3}\right) & \cos \left(\omega t-\frac{2 \pi}{3}\right) & 1 \\
\sin \left(\omega t+\frac{2 \pi}{3}\right) & \cos \left(\omega t+\frac{2 \pi}{3}\right) & 1
\end{array}\right]\left[\begin{array}{c}
u_d \\
u_q \\
u_0
\end{array}\right]
$$
使用方式
一般matlab的dq模块默认是使用90 degree behind phase A axis,如果以基于余弦的派克变换,则将模块的变换选择为Aligned with phase A axis,但是一定要注意,前面使用的正变换和后面使用的逆变换的变换方式一定要对应好。这样最后的控制才能同频同相。文章来源地址https://www.toymoban.com/news/detail-465840.html
到了这里,关于Matlab的dq变换模块到底选哪一种变换方式?90 degree behind phase A axis和 Aligned with phase A axis有什么区别?的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!