如何用matlab做高精度计算？【第二辑】

高精度计算是一种程序设计的算法。由于中央处理器的字长限制，如32位CPU中一个整数最大只能取值4,294,967,295（=2^32-1），因此在超范围数值计算中，往往要采用模拟手段。通常使用分离字符的方法来处理数字数组。

维基百科【高精度计算】

在上一辑中，给大家介绍了如何使用matlab自带工具箱实现高精度计算(详见：如何用matlab做高精度计算？【第一辑】)。本期给大家带来两款来自File Exchange源代码共享资源库的宝贝，它们都是出自大神John D'Errico之手。前者是专门用于处理超大值整数运算的 —— Variable Precision Integer Arithmetic，对应数据类型为vpi，后者是用于处理浮点数计算的 —— HPF (a big decimal class)，对应数据类型为hpf。

接下来咱们就一起来揭开这两款工具箱的神秘面纱。

一、Variable Precision Integer Arithmetic

从名称不难看出，VPI工具箱是专门用于处理整数相关计算的，而大神John D'Errico开发VPI工具箱的目的也很简单，因为他不能用MATLAB符号处理工具箱，而他的这种款工具箱意义已经超越了其初衷。正所谓前人栽树，后人乘凉。有了VPI这款工具箱，原则任意的大整数计算在MATLAB都可以实现。接下来就一起来看看如何使用这款工具吧！

1.1 创建VPI类型数据

vpi类型数据创建有以下四种方法：

① num = vpi; 创建一个值为0的变量；

② num = vpi([]); 创建一个空的vpi变量

③ num = vpi(1415926); 将整数转换成vpi类型数字

④ num = vpi('12345678900987654321'); 将符号型整数转换成vpi类型数字

注：为了防止因MATLAB精度限制造成超大整数无法完整准确表达，建议对于超大整数使用符号型整数来处理。

1.2 类型数据类型转换

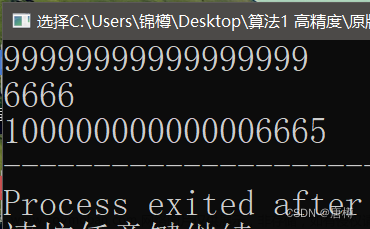
使用double或single可以将vpi型数据转换成MATLAB的double或single型，但此操作会造成数据精度损失，如下图所示：

1.3 VPI类型数据的运算

vpi类型的数据除支持四则运算、比较运算外，还支持指数、开方等复杂运算规则，因vpi型数据是整数型数据，开方时只会得到最近的整数结果。

1.4 VPI类型数据进制转换

vpi型数据还有特殊功能，支持数据进制转换，相关的函数有：

vpi2base：vpi型数据到任意进制转换；

vpi2bin：vpi型数据到二进制转换；

vpi2english：vpi型数据的英语读法；

base2vpi：任意进制到vpi型数据；

bin2vpi：二进制到vpi型数据；

1.5 vpi类所支持的方法

Methods for class vpi:
abs                double             gcd                isprime            lt                 ne                 rdivide            sum                vpi2english        
ceil               eq                 ge                 isunit             max                nthroot            rem                times              
comparemagnitudes  exp                gt                 iszero             min                num2str            round              trailingdigit      
conv               factor             isequal            lcm                minus              order              shiftdec           uminus             
cumprod            factorial          iseven             le                 mod                plus               sign               unique             
cumsum             find               isfinite           leadingdigit       mpower             power              single             uplus              
digits             fix                isinf              log                mrdivide           prod               sort               vpi                
disp               floor              isnan              log10              mtimes             quotient           sortrows           vpi2base           
display            full               isnumeric          log2               nchoosek           randint            sqrt               vpi2bin

除了上面介绍的内容外，VPI工具箱更多功能函数小伙伴自己去探究吧，因篇幅不宜过长，咱就介绍到此。总而言之，VPI工具箱非常强大，能满足在matlab中的绝大部分整数计算需求。

二、High Precision Floating

大神John D'Errico在分享了超大整数计算工具箱后又分享了任意精度浮点数计算工具箱 —— High Precision Floating (HPF)。与上一期介绍的如何用matlab做高精度计算？【第一辑】一样，作为浮点数计算，首先需要人为自定义计算所需要的精度，如果不设置，则会使用默认的精度进行计算。

1.1 hpf类型数据数据精度定义

hpf型数据精度设置涉及到两个函数 —— DefaultNumberOfDigits与

DefaultDecimalBase。前者用于设置浮点数位数，后者用于设置存储数字的字段长度。

DefaultNumberOfDigits使用方式如下：

DefaultNumberOfDigits(nDigits,sDigits)，其中nDigits是实际显示浮点数位数，sDigits是保护位数，因为浮点数计算比纯整数计算误差更不易掌控，因此数据实际显示位数后再加sDigits位数据来确保前面数据的准确性。

使用方式：
① DefaultNumberOfDigits(nDigits)
② DefaultNumberOfDigits(nDigits,sDigits)
③ DefaultNumberOfDigits nDigits
④ DefaultNumberOfDigits nDigits sDigits

DefaultDecimalBase使用方式如下：

DefaultDecimalBase(DBase)，其中，DBase只能取1，2，3，4，5或6，DBase取不同值，能表示最大浮点数位数各不相同，如下：

DBase = 1 --> 3.6e14 decimal digits
DBase = 2 --> 3.6e12 decimal digits
DBase = 3 --> 3.6e10 decimal digits
DBase = 4 --> 3.6e8 decimal digits
DBase = 5 --> 3.6e6 decimal digits
DBase = 6 --> 36000 decimal digits

DBase越大，计算速度越快，反正越慢。故默认DBase为6，对于计算不是特别大时，建议不要修改Dbase。

2.2 hpf类型数据的创建

hpf类型数据创建有以下五种方法：

① num = hpf; 创建一个值为0的变量；

② num = hpf([]); 创建一个空的hpf变量

③ num = hpf(3.141592653589793238462); 将整数转换成hpf类型数字

④ num = hpf('3.141592653589793238462'); 将符号型整数转换成hpf类型数字

⑤ num = hpf('3.141592653589793238462',num); 将符号型整数转换成hpf类型数字，并指定位数为num。

和vpa函数一样，如果需要创建高精度hpf型数据，建议不要采用方法③，因为会受matlab的浮点数有效位数的影响导致被截断。

2.3 hpf类所支持的方法

和vpi类型数据一样，hpf类型数据也是一种数据类，在命令窗口输入methods('hpf')即可查看hpf所支持的所有方法。

Methods for class hpf:
abs                asinh              csc                erf                int32              lt                 plus               sign               uint32             
acos               atan               cscd               exp                int64              lu                 power              sin                uint64             
acosd              atand              csch               factorial          int8               mantissa           prod               sind               uint8              
acosh              atanh              cubrt              fix                isfinite           max                rank               single             uminus             
acot               augmentdigits      cumprod            floor              isinf              min                rat                sinh               uplus              
acotd              ceil               cumsum             fminsearch         isnan              minus              rdivide            sort               vpi                
acsc               chol               det                fractionalpart     isnumeric          mod                reciprocal         sqrt               
acscd              cos                diag               full               iszero             mpower             round              sum                
adjustdecimalbase  cosd               disp               ge                 le                 mrdivide           roundn             tan                
asec               cosh               display            gt                 linspace           mtimes             rref               tand               
asecd              cot                double             hpf                log                ne                 sec                tanh               
asin               cotd               eps                int16              log10              nthroot            secd               times              
asind              coth               eq                 int2str            log2               num2str            sech               uint16             


Static methods:
eye                ones               ten                zeros

2.4 hpf型数据应用案例 (来源于作者提供的帮助文档)

使用Chudnovsky公式计算π：

DefaultNumberOfDigits 5000 10
DefaultDecimalBase 5
a1 = hpf(13591409); % small integers, so exact
a2 = hpf(545140134);
a3 = hpf(640320);
a4 = a3.*a3.*a3;
num = hpf(1);
den = sqrt(a4);
tol = eps(num);
piinv = hpf(0);
k = 0;
while 1


  piterm = num.*(a1+a2.*k)./den;
  piinv = piinv + piterm;


  if abs(piterm) < tol
    break
  end


  k = k + 1;
  num = num.*prod(hpf(6*k+(-5:0)));
  den = den.*a4.*(3*k-2).*(3*k-1).*(3*k).*hpf(k).^3;


  num = -num;


end
piest = reciprocal(12.*piinv)

Ref: en.wikipedia.org/wiki/Chudnovsky_algorithm

以上就是matlab做高精度计算第二辑的全部内容，更多地应用伙伴们自己去开发，本文仅是作为引子的作用。下一辑将会为大家介绍一款收费的高精度计算工具箱 —— Multiprecision Computing Toolbox，执行效率远超matlab自带的vpa工具箱。欲知后事如何，且看下回分解！

参考资料：

[1] www.mathworks.com/help/symbolic/vpa.html

[2] https://zh.m.wikipedia.org/zh-hans/高精度计算

如需转载，请在懂科学的程序员公众号中回复“转载”获取授权！文章来源地址https://www.toymoban.com/news/detail-466351.html