传统图片超分算法——双三次插值 (Bicubic)、附C++源码-Toy模板网

这篇具有很好参考价值的文章主要介绍了传统图片超分算法——双三次插值 (Bicubic)、附C++源码。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

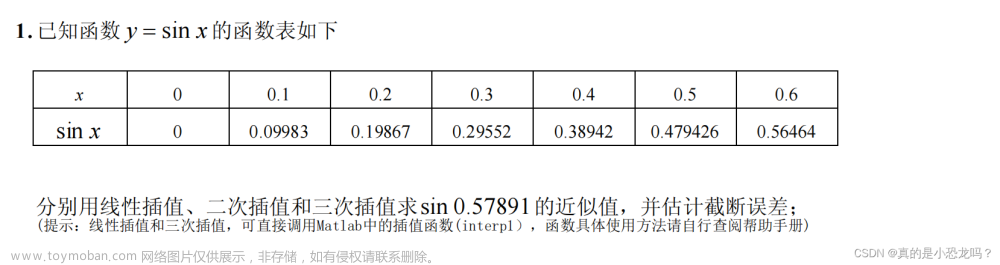
~~呼，花了一个下午，终于是写完加调试完了所有的代码。~~

双三次插值介绍

之前我写的这篇博客中讲了什么是超分，并实现了单线性插值算法和双线性插值算法。在这里将再介绍一种插值算法——双三次插值算法。

首先，双三次插值法需要参考16个点（4x4），因此插值效果会比双线性插值法要好，但同时时间开销也会更大。在 OpenCV 中，可在 cv::resize 函数中使用 cv::INTER_CUBIC 选项选择使用双三次插值算法改变图像大小。

在学习的过程中，我参考了这篇博客，其中的插值算法写成表达式的形式为：
$f(x,y)=\sum_{i=0}^3\sum_{j=0}^3f(x_i,y_j)W(x-x_i)W(y-y_j)$
其中，(x,y) 表示待插值的像素点的坐标，f(x,y)表示经过计算待插值像素点应该插入的值， $x_i,y_j)$ $i, j = 0, 1, 2, 3$ 表示待插值点附近的 4x4 领域的点。

$W$ 函数称为 BiCubic 函数。与该博客中不同的是，原博客中的像素点可以是浮点数，而在 OpenCV 中坐标只能为整数。因此在这里 $W$ 函数需要做个变换。

原博客中的 $W$ 函数：
$W(x)=\left\{ \begin{matrix} (a+2)|x|^3-(a+3)|x|^2+1 \qquad|x|\le1\\ a|x|^3-5a|x|^2+8a|x|-4a\qquad1<|x|<2\\ 0\qquad \qquad \qquad else\\ \end{matrix} \right.$

在这里使用的 $W$ 函数：
$W(x)=\left\{ \begin{matrix} (a+2)|x/t|^3-(a+3)|x/t|^2+1 \qquad |x|\le t\\ a|x/t|^3-5a|x/t|^2+8a|x/t|-4a\qquad t<|x|<2t \\ 0\qquad \qquad \qquad else\\ \end{matrix} \right.$

其中 $t$ 为超分放大倍数， $a$ 为指定的值，OpenCV 源码中给的是 -0.75。

代码实现

首先是需要循环遍历每个像素点，逐个计算像素点的值。

进一步地，如何计算像素点的值呢？例如，下图中绿色的点是原图像上的像素点，红色的点是待计算的点，则用黄色框起来的点为参考的像素点。假设其坐标为(i,j)（在dst上，即保存超分结果的图像上），以行为例，则参考src的行号如下图所标注。对于列也是同理。因此我们知道了上述表达式中 $x_i$ 和 $y_j$ 的所有取值。
传统图片超分算法——双三次插值 (Bicubic)、附C++源码 $W(x-x_i)$ 中的 $x-x_i$ 表示当前像素点距离参考像素点的 $x$ 方向上的距离（ $y$ 方向同理）。根据 $W$ 函数的表达式可以判断出，这个距离应该要小于两倍的 $t im es$ （放大倍数）。以左边的参考点为例（向右也是同理），在dst 图像中，对于离待计算点最近的左边的像素点，它们的 $x$ 方向上的距离为 $i\%times$ 。又因为在 dst 图中，两个绿色的点之间的间距为放大倍数，因此计算点离最左边的参考点的距离为 $i\%times+times$ 。同时考虑到右侧的点，可以写成更加一般的形式： $i\%times-i*times$ 。其中 $i = - 1, 0, 1, 2$ 。对于列也是同理。

(注：在代码中，为了与逐个枚举像素点的循环变量区分开，此处的 i j 会写成 r c。其中 r 代表 row，表示行； c 代表 col，表示列。)

以下是完整的代码：

//权重计算函数
//输入：x:自变量的值  times: 图片超分倍数
//返回值：W(x)计算之后的值
double W(int x,int times){
    
    x=std::abs(x);

    //OpenCV 中给的是 -0.75
    double a=-0.75;
    double abs_=std::abs((double)x/(double)times);
    
    if(x>=2*times) return 0.0;
    else if(x>times){
        double ans=a*(abs_)*(abs_)*(abs_)-5*a*(abs_)*(abs_)+8*a*(abs_)-4*a;
        return ans;
    }
    else{
        double ans=(a+2)*(abs_)*(abs_)*(abs_)-(a+3)*(abs_)*(abs_)+1;
        return ans;
    }

    //不会执行到这里的，哈哈
    return -1.0f;
}

//双三次插值
//输入：原图像（单通道），超分倍数
//返回值：超分后的图像
cv::Mat biCubicInterp(const cv::Mat &src, int times){
    cv::Mat dst=cv::Mat::zeros(cv::Size(src.cols*times,src.rows*times),CV_8UC1);

    for(int i=0;i<dst.rows;i++){
        for(int j=0;j<dst.cols;j++){
            double val=0.0;

            //利用周围16个像素点计算插值
            for(int r=-1;r<=2;r++){
                //如果参考点超出图像范围，则舍弃
                if(i/times+r<0 || i/times+r>=src.rows) continue;
                
                for(int c=-1;c<=2;c++){
                    //如果参考点超出图像范围，则舍弃
                    if(j/times+c<0 || j/times+c>=src.cols) continue;
                    
                    val+=(src.at<uchar>(i/times+r,j/times+c)*W(i%times-r*times,times)*W(j%times-c*times,times));
                }
            }

            //防止越界溢出
            if(val>255) val=255;
            if(val<0) val=-val;
            
            dst.at<uchar>(i,j)=(unsigned char)val;
        }
    }
    return dst;
}