【题目描述】
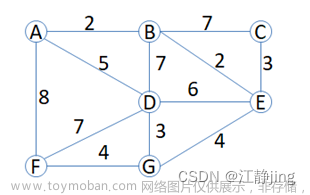
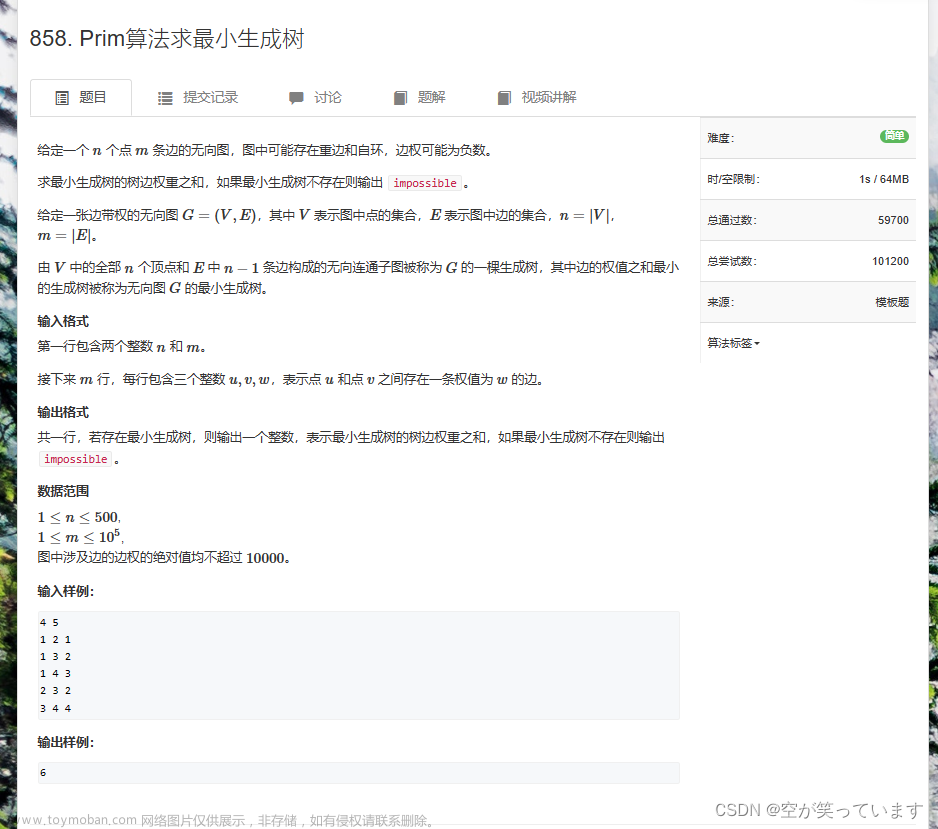
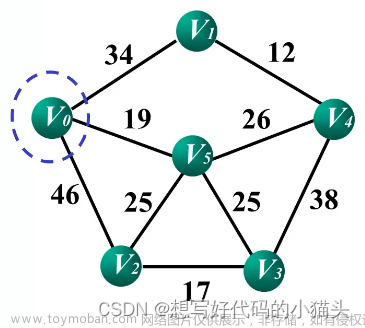
给定一个 n 个点 m 条边的无向连通图。图中可能存在重边和自环,边权可能为负数。
利用Prim算法求此种无向连通图的最小生成树的树边权重之和。
【输入格式】
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
【输出格式】
共一行,输出一个整数,表示无向连通图的最小生成树的树边权重之和。
【数据范围】
1≤n≤500,
1≤m≤10^5,
图中涉及边的边权的绝对值均不超过 10000。
【算法代码】
此代码由儿子写于初二暑假期间(2019年7月1日至7月10日间)。
#include <bits/stdc++.h>
using namespace std;
const int maxn=505;
int e[maxn][maxn],dis[maxn],st[maxn];
int inf=0x3f3f3f3f;
int cnt,sum;
int t1,t2,t3,tmp,zx;
int main() {
int n,m; //n:Number of vertices, m:Number of edges
cin>>n>>m;
//Initialize the graph with an adjacency matrix
for(int i=1; i<=n; i++) //n:Number of vertices
for(int j=1; j<=n; j++)
if(i==j) e[i][j]=0;
else e[i][j]=inf;
//Input edges and weights
for(int i=1; i<=m; i++) { //m:Number of edges
cin>>t1>>t2>>t3; //from,to,weight
e[t1][t2]=min(e[t1][t2],t3);
e[t2][t1]=min(e[t1][t2],t3);
}
//Initialize the dis array
for(int i=1; i<=n; i++)
dis[i]=e[1][i];
st[1]=1;
cnt++;
while(cnt<n) {
zx=inf;
for(int i=1; i<=n; i++) {
if(st[i]==0 && dis[i]<zx) {
zx=dis[i];
tmp=i;
}
}
st[tmp]=1;
cnt++;
sum+=dis[tmp];
for(int k=1; k<=n; k++) { //update dis array
if(st[k]==0 && dis[k]>e[tmp][k])
dis[k]=e[tmp][k];
}
}
cout<<sum<<endl;
return 0;
}
/*
in:
6 9
2 4 11
3 5 13
4 6 3
5 6 4
2 3 6
4 5 7
1 2 1
3 4 9
1 3 2
out:
19
-------
in:
5 10
1 2 8
2 2 7
2 1 1
3 4 3
4 4 -10
1 3 -9
5 2 -4
3 1 0
1 4 8
4 4 7
out:
-9
*/
【算法拓展】
若给出的无向图是连通图或非连通图,且图中可能存在重边和自环,边权可能为负数的情形,则可参考YXC大佬的经典Prim算法代码。
#include<iostream>
#include<cstring>
using namespace std;
const int inf=0x3f3f3f3f;
const int maxn=505;
int g[maxn][maxn],dis[maxn];
bool st[maxn];
int n,m,ans;
void prim() {
memset(dis,inf,sizeof dis);
for(int i=0; i<n; i++) {
int t=-1;
for(int j=1; j<=n; j++) {
if(!st[j]&&(t==-1||dis[t]>dis[j]))
t=j;
}
st[t]=true;
if(i && dis[t]==inf) {
cout<<"impossible"<<endl;
return;
}
if(i) ans+=dis[t];
for(int j=1; j<=n; j++) {
dis[j]=min(dis[j],g[t][j]);
}
}
cout<<ans<<endl;
}
int main() {
cin>>n>>m;
memset(g,inf,sizeof g);
while(m--) {
int a,b,c;
cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c);
}
prim();
return 0;
}
/*
in:
10 20
5 3 -8
9 6 -1
1 3 -1
8 7 -6
5 4 6
7 7 -4
4 5 2
10 7 -4
2 1 9
7 10 10
4 5 6
8 7 -7
4 2 -3
9 6 6
5 1 0
7 6 5
5 4 -3
10 8 3
5 3 2
7 8 -7
out:
impossible
-------
in:
5 10
1 2 8
2 2 7
2 1 1
3 4 3
4 4 -10
1 3 -9
5 2 -4
3 1 0
1 4 8
4 4 7
out:
-9
*/
【参考文献】
https://blog.csdn.net/Yu_iChan/article/details/127173866
https://www.acwing.com/problem/content/860/
https://www.acwing.com/blog/content/405/
https://www.acwing.com/solution/content/38312/
https://www.acwing.com/problem/content/solution/860/1/
文章来源:https://www.toymoban.com/news/detail-466720.html
文章来源地址https://www.toymoban.com/news/detail-466720.html
到了这里,关于求无向连通图的最小生成树 ← Prim算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!