模糊性常常是信息浓缩所致,目的是为了提高交换的概率,所以不是毫无用处,而是积极的特性。模糊是指客观事物差异的中间过渡中的“不分明性”或“亦此亦彼性”。模糊数学是用来处理涉及模糊概念的问题,尝试使用某种方法将模糊的概念量化,方便进行处理计算。模糊综合评价是模糊数学在评价类问题的一大应用,也就是处理涉及模糊概念的评价类问题。文章主要借鉴B站数模交流,侵权立删。
目录
模糊数学的基本概念
隶属函数的确定(关键)
1.模糊统计方法
2.模糊分布
模糊集合分类
常见模糊分布及其图形
3.其他确定方法
模糊综合评价
概念
一级模糊综合评价方法
一般步骤
例题:一级模糊综合评价在人事考核中的应用
多级模糊综合评价方法
一般步骤(以二级模糊综合评价为例)
例题:多级模糊综合评价在人事考核中的应用
模糊综合评价优缺点
模糊数学的基本概念
集合:具有某种特定属性的对象集体,通常用大写字母:A,B,C等表示。
论域:对局限于一定范围内进行讨论的对象的全体,通常用大写字母:U,V,X,Y等表示。论域U中的每个对象u称为U的元素。
模糊子集:
设U是论域,称映射,确定了U上的模糊子集A。映射称为A的隶属函数,称为x对A的隶属程度,简称隶属度。模糊子集通常简称模糊集。

隶属函数:
隶属函数是隶属度对各个元素的函数,定义域是我们所研究的元素,函数值就是隶属度。隶属度的范围是[0,1],其值越大,就代表越属于这个模糊集合。

模糊集的表示方法:

隶属函数的确定(关键)
1.模糊统计方法
类似于统计学中的大样本实验法,根据概念所占比例确定其对应隶属度。
例如:我现在要确立“青年人”的隶属函数。以年龄为论域U,A是“青年人”模糊集合,选取岁。
①调查若干人选,各自认真考虑“青年人”的含义之后,提出“青年人”最合适的年龄区间(随机地将模糊概念明确化)。表4记录了129人关于“青年人”年龄区间的调查结果。如果设A=“青年人",那么表中每个区间就是每次试验中的A。

②对于,求出对A的隶属频率稳定值,作为对A的隶属度值。
比如,对于(岁),根据对表4的随机抽样得知:当样本总数 时,样本区间覆盖27的频数,相应的隶属频率,具体数据参见表5。以n为横坐标、f为纵坐标绘制图形(图4)可以发现,对A的隶属频率稳定在0.78附近,因此“27(岁)”对模糊集“青年人”A的隶属度确定为0.78。

类似的,对,求出x对A的隶属频率值,作为x对A的隶属度值,见表6。

③根据表6的数据,可做出模糊集A=“青年人”的隶属函数曲线,如图5。

2.模糊分布
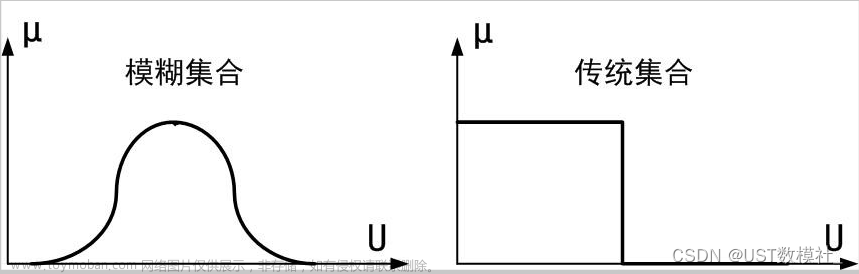
如果考虑以实数集R作论域,通常把实数集R上模糊集的隶属函数称为模糊分布。当所讨论的客观模糊现象的隶属函数与某种给定的模糊分布相类似时,即可选择这个模糊分布作为所求的隶属函数,然后再通过先验知识或数据实验确定符合实际的参数,从而得到具体的隶属函数。
例如,我们可以把左图看作给定的模糊分布,右图是我们要讨论的客观模糊现象的隶属函数,那么我们就可以选择左图的模糊分布作为所求的隶属函数,并通过先验知识或数据实验确定符合实际的参数得到具体的隶属函数。


模糊集合分类
模糊集合主要有三类,分别为偏小型,中间型和偏大型。可以说也就类似于理想解法(TOPSIS)方法中的极大型、极小型、中间型、区间型指标。
常见模糊分布及其图形
1.矩形分布或半矩形分布
①偏小型
文章来源地址https://www.toymoban.com/news/detail-467181.html
②偏大型
③中间型

2.梯形分布或半梯形分布
①偏小型
②偏大型
③中间型

3.K次抛物型或半抛物型分布
①偏小型

②偏大型

③中间型


4.高斯分布或半高斯分布
①偏小型

②偏大型

③中间型


5.柯西分布或半柯西分布
①偏小型

②偏大型

③中间型


6.岭型分布或半岭型分布
①偏小型

②偏大型

③中间型


3.其他确定方法
德尔菲(Delphi)法、专家评分法、二元对比排序法等。
不管模糊集合是哪一种类型,求得的隶属度越大,属于这个集合的程度也越大。事实上,隶属函数也不是唯一的,不同的人或者说不同大小的样本,得出来的隶属函数有可能是不同的,有着主观的色彩。
模糊综合评价
模糊综合评价法(Fuzzy Comprehensive Evaluation)是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
当评价的指标中有认为通过经验赋予数值的变量,如评判人是否优秀、食品是否安全等,则可以考虑用模糊综合评价。
模糊综合评价将人的主观经验判断和数学理论的严谨推理有效结合,适合于社会调查、市场调查、市场咨询、教育改革、企业员工职务升迁、评先晋级等领域的研究工作。
概念
- 因素集(评价指标集):,与评价事务相关的因素有n个。
- 评语集(评价的结果):,所有可能出现的评语有m个。
- 权重集(指标的权重):,各种因素的作用和影响力不同。
| 模糊综合评价 | 一级模糊综合评价 |
| 多级模糊综合评价 |
一级模糊综合评价方法
一般步骤
- 确定因素集
- 确定评语集
- 进行单因素评价得到
- 构造综合评价矩阵
- 综合评价,对权重矩阵,计算,并根据最大隶属度原则做出评价。
最大隶属度原则:相对于那个模型的隶属度最大,那么就属于哪个模型。
例题:一级模糊综合评价在人事考核中的应用

1、比如由群众评议打分来确定,
上式子表示,参与打分的群众当中,有10%的人认为政治表现优秀,50%的人认为政治表现良好,40%的人认为政治表现一般,认为政治表现较差或差的人为0,用同样的方法对其它因素进行评价。
2、由部门领导打分来确定
3、由考核组员打分来确定
以为构成评价矩阵
它是从因素集U到评语集V的一个模糊关系矩阵。
4、模糊综合评判。进行矩阵合成运算
取数值最大的评语作为综合评判结果,则评判结果为“良好”。
多级模糊综合评价方法
一般步骤(以二级模糊综合评价为例)
- 将因素集划分为若干组,得到,其中,。称为第一级因素集。
- 设评语集,先对第二级因素集的个因素进行单因素评价,得到单因素评价矩阵,设的权重为,求得综合评价为:
- 再对第一级因素集进行综合评价,设其权重为则总评价矩阵为:,从而得到综合评价,按照最大隶属度原则即得相应评语。
例题:多级模糊综合评价在人事考核中的应用

首先确定各个子因素集模糊综合判断矩阵,就得到了下表中的数据。

一是因素过多,它们的权数分配难以确定;另一方面,即使确定了权分配,由于需要满足归一化条件,每个因素的权值都小,对这种系统,可以采用多层次模糊综合评价的方法。我们这里对于人事考核而言,采用二级系统就足以解决问题了。

设专家指标额的权重,一级指标的权重为:
二级指标的权重为:
对各因素进行一级模糊综合评价为:
最后再进行二级模糊综合评价:
所以根据最大隶属度原则,认为对该员工的评价为“良好”。
模糊综合评价优缺点
 文章来源:https://www.toymoban.com/news/detail-467181.html
文章来源:https://www.toymoban.com/news/detail-467181.html
到了这里,关于模糊综合评价的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!