数据结构--图的存储结构-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构--图的存储结构。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

系列文章目录

第九话数据结构之图的存储

文章目录

一、了解什么是图
二、图的定义和基本术语
三、存储结构之邻接矩阵
- 1.邻接矩阵的介绍
- 2.邻接矩阵的创建
- 3.主函数中实现
四、存储结构之邻接表
- 1.邻接表的介绍
- 2.邻接表的创建
- 3.在主函数中实现
五、总结

前言

一切尽在图结构

图的应用非常广泛，可以用图来表示物体的外形、城市的布局、经济的增长、程序的流程，甚至心情的好坏。

自然界的很多现象都可以抽象成一个图结构，计算机网络可以抽线成一张网络图，设计程序时就会画一张流程图，航空公司的航班路线也是一张图，旅游公司的行程也是一张流程图，有机化学分子也可用图来表示，图无处不在。

一、了解什么是图

图是一种比线性表和树更为复杂的数据结构，在图结构中，节点之间的关系可以是任意的，任意两个元素之间都可能相关，所以图结构被用于描述各种复杂的数据对象。

图是一种数据结构。图的基本操作主要有创建、插入、删除、查找等。从图的逻辑结构定义可知，无法将图中的顶点排列成一个唯一的线性序列。

可将任意一个顶点看成是图的一个顶点，同理，对于任意一个顶点而言，其邻接点之间也不存在顺序关系。但为了便于对图进行操作，需要将图中的顶点按任意序列排列起来。

二、图的定义和基本术语

1、有向图和无向图

图的定义：用顶点集合和边集合组合起来的集合称为图

对于图而言，分为有向图和无向图

有向图如下：

数据结构--图的存储结构

无向图如下：

数据结构--图的存储结构

有向图的介绍:：

有向图：在有向图中，顶点对用一对尖括号括起来，即<x,y>,这个是有序的，x是有向边的起始点，y是有向边的终点。<x.y>总体表示从顶点x到顶点y的一条有向边，<x,y>带表一条边,因为是有向的，所以<x,y>和<y,x>是两条不同的边。

无向图的介绍：

无向图：在无向图中，顶点对用一对圆括号括起来，即(x,y),这个是无序的，由于是无向的。所以这条边没有特定的方向，(x,y)和(y,x)是同一条边。

2、图的基本术语

无向完全图：对于无向图，如果任意两顶点都有一条边直接连接，则称该图为无向完全图。顶点n与边a的关系为：a = n(n-1)/2

有向完全图：对于有向图，如果任意两顶点之间都有方向互为相反的两条弧相连接，则称该图为有向完全图。顶点n与弧a的关系为：a = n(n-1)

三、存储结构之邻接矩阵

1、邻接矩阵

邻接矩阵是表示顶点之间相邻关系的矩阵，用一维数组存储图中顶点的信息，用矩阵表示图中各顶点之间的邻接关系。

在无向图中，若两顶点之间是连通的，则用1表示，否则用0表示。

在有向图中，若A能够到B，则A到B表示1，没有方向连接的用0表示。

数据结构--图的存储结构

2、无向图的邻接矩阵存储

首先我们把ABCD分别编序为0，1，2，3

1.邻接矩阵存储

#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 100
//无向图的邻接矩阵
typedef struct
{
	char data[MAXSIZE];//顶点数组
	int arc[MAXSIZE][MAXSIZE];//邻接矩阵
	int vexnum, edgenum;//当前的定点数和边数

}MGraph;

2.邻接矩阵的创建

//图的邻接矩阵的创建
void CreateMgrapg(MGraph *p)
{
	int i, j, k;
	printf("输入定点数和弧数：");
	scanf("%d %d", &p->vexnum,&p->edgenum);//输入顶点数和弧数
	printf("输入所有顶点的信息：");
	for (i=0; i<p->vexnum;i++)
    {
		scanf(" %c",&p->data[i]);
	}
	for (i = 0;i < p->vexnum;i++){
		for (j = 0;j<p->vexnum;j++){
			p->arc[i][j] = 0;
		}
	}
	for (k=0; k < p->edgenum; k++)
	{
		printf("输入第%d弧的两个顶点的序号,格式（i j）：",k+1);
		scanf("%d %d", &i, &j);
		p->arc[i][j] = 1;
		p->arc[j][i] = 1;//去掉这个代表有向图
	}
}

3.邻接矩阵的输出及在主函数中实现

void print(MGraph g)
{
	int i,j;
	for (i = 0; i < g.vexnum; i++)
	{
		for (j = 0; j < g.vexnum; j++)
		{
			printf("%-3d", g.arc[i][j]);
		}
		printf("\n");
	}
}
int main()
{
	MGraph g;
	CreateMgrapg(&g);
	print(g);
	return 0;
}

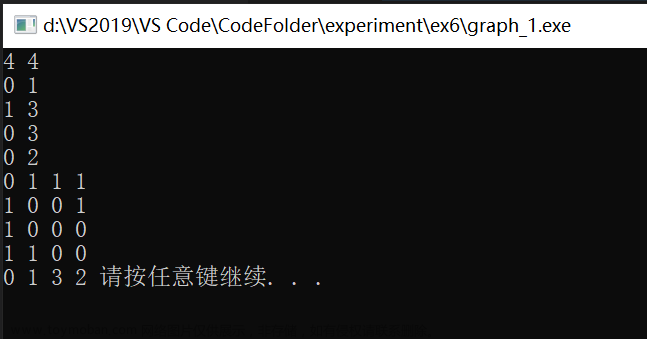
4.实现如下

数据结构--图的存储结构

5.完整代码如下

#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 100
//无向图的邻接矩阵
typedef struct
{
	char data[MAXSIZE];//顶点数组
	int arc[MAXSIZE][MAXSIZE];//邻接矩阵
	int vexnum, edgenum;//当前的定点数和边数

}MGraph;
//图的邻接矩阵的创建
void CreateMgrapg(MGraph *p)
{
	int i, j, k;
	printf("输入定点数和边数：");
	scanf("%d %d", &p->vexnum,&p->edgenum);//输入顶点数和边数
	printf("输入所有顶点的信息：");
	for (i=0; i<p->vexnum;i++)
    {
		scanf(" %c",&p->data[i]);
	}
	for (i = 0;i < p->vexnum;i++){
		for (j = 0;j<p->vexnum;j++){
			p->arc[i][j] = 0;
		}
	}
	for (k=0; k < p->edgenum; k++)
	{
		printf("输入第%d边的两个顶点的序号,格式（i j）：",k+1);
		scanf("%d %d", &i, &j);
		p->arc[i][j] = 1;
		p->arc[j][i] = 1;//去掉这个可以表示有向图
	}
}
void print(MGraph g)
{
	int i,j;
	for (i = 0; i < g.vexnum; i++)
	{
		for (j = 0; j < g.vexnum; j++)
		{
			printf("%-3d", g.arc[i][j]);
		}
		printf("\n");
	}
}
int main()
{
	MGraph g;
	CreateMgrapg(&g);
	print(g);
	return 0;
}

四、存储结构之邻接表

1、邻接表

邻接表是图的一种链式存储结构。在邻接表中，对图中每个顶点建立一个单链表，把相邻的顶点放在这个链表中。

数据结构--图的存储结构

2、有向图的邻接表存储

首先我们把ABCD分别编序为0，1，2，3

1.邻接表存储

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
//有向图邻接表的存储
typedef char VertexType;
typedef struct node{//定义边表结点
	int adjvex;//邻接点域
	struct node *next;//指向下一个邻接点域的指针域
}EdgeNode;
typedef struct vexnode{//定义顶点表结点
	VertexType data;//顶点域
	EdgeNode *firstedge;//指向第一条边结点
}VHeadeNode;
typedef struct{
	VHeadeNode adjlist[MAXSIZE];/*邻接表头结点数组*/
	int n,e;//顶点数，边数
}AdjList;

2.邻接表的创建

void GreateAGraph(AdjList *g){
	int i,j,k;
	printf("请输入图的顶点数和边数：");
	scanf("%d %d",&g->n,&g->e);
	printf("请输入图的所有顶点信息：");
	for(i=0;i<g->n;i++){
		scanf(" %c",&(g->adjlist[i].data));//给图的每个结点的顶点域赋值
		g->adjlist[i].firstedge = NULL;//首先点的边表头指针都设为空
	}
	EdgeNode *p;
	for(k=0;k<g->e;k++){
        printf("请输入第%d条边对应的两个顶点的序号,格式（i j）:",k+1);
		scanf("%d %d",&i,&j);
		p = (EdgeNode*)malloc(sizeof(EdgeNode));
		p->adjvex = j;
		p->next = g->adjlist[i].firstedge;//头插法
		g->adjlist[i].firstedge = p;
	}
}

3.邻接表的输出及在主函数中实现

/邻接表的输出
void printadj(AdjList *g){
	int i;
	EdgeNode *p;
	for(i=0;i<g->n;i++){
		printf("%2d [%c]",i,g->adjlist[i].data);
		p = g->adjlist[i].firstedge;
		while(p!=NULL){
			printf("-->[%d]",p->adjvex);
			p = p->next;
		}
		printf("\n");
	}
}
int main() {
	AdjList G;
	GreateAGraph(&G);//创建有向图
	printadj(&G);
	return 0;
}

4.实现如下

数据结构--图的存储结构

5.完整代码如下：

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
//有向图邻接表的存储
typedef char VertexType;
typedef struct node{//定义边表结点
	int adjvex;//邻接点域
	struct node *next;//指向下一个邻接点域的指针域
}EdgeNode;
typedef struct vexnode{//定义顶点表结点
	VertexType data;//顶点域
	EdgeNode *firstedge;//指向第一条边结点
}VHeadeNode;
typedef struct{
	VHeadeNode adjlist[MAXSIZE];/*邻接表头结点数组*/
	int n,e;//顶点数，边数
}AdjList;

//有向图邻接表的创建
void GreateAGraph(AdjList *g){
	int i,j,k;
	printf("请输入图的顶点数和边数：");
	scanf("%d %d",&g->n,&g->e);
	printf("请输入图的所有顶点信息：");
	for(i=0;i<g->n;i++){
		scanf(" %c",&(g->adjlist[i].data));//给图的每个结点的顶点域赋值
		g->adjlist[i].firstedge = NULL;//首先点的边表头指针都设为空
	}
	EdgeNode *p;
	for(k=0;k<g->e;k++){
        printf("请输入第%d条边对应的两个顶点的序号,格式（i j）:",k+1);
		scanf("%d %d",&i,&j);
		p = (EdgeNode*)malloc(sizeof(EdgeNode));
		p->adjvex = j;
		p->next = g->adjlist[i].firstedge;//头插法
		g->adjlist[i].firstedge = p;
	}
}
//邻接表的输出
void printadj(AdjList *g){
	int i;
	EdgeNode *p;
	for(i=0;i<g->n;i++){
		printf("%2d [%c]",i,g->adjlist[i].data);
		p = g->adjlist[i].firstedge;
		while(p!=NULL){
			printf("-->[%d]",p->adjvex);
			p = p->next;
		}
		printf("\n");
	}
}
int main() {
	AdjList G;
	GreateAGraph(&G);//创建有向图
	printadj(&G);
	return 0;
}

五、总结

邻接矩阵：

优点：很容易确定任意两个顶点之间是否有边相邻

缺点：不便添加和删除顶点、不便统计边的数目

邻接表

优点：方便增加和删除顶点、易于统计边的数目、空间效率高

缺点：不便判断顶点间是否有边、不便计算有向图中各个顶点的度

总体注意：一个图的邻接矩阵表示是唯一的，但其邻接表表示不是唯一的。因为邻接表表示中，链接次序取决于算法、边和输入顺序文章来源地址https://www.toymoban.com/news/detail-467197.html

到了这里，关于数据结构--图的存储结构的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！