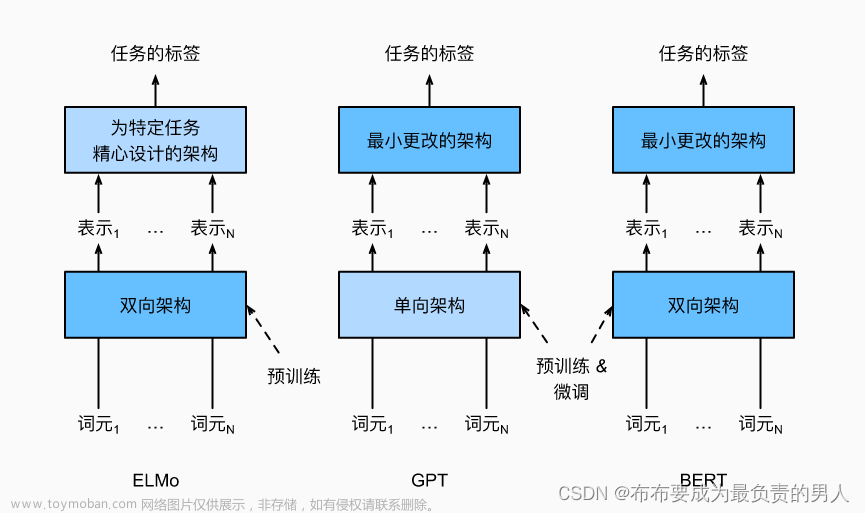
在学习Transformer模型过程中不可避免的一个过程便是要对序列进行位置编码,在Transformer中分为固定位置编码与可学习的位置编码,其一般采用固定位置编码中的正余弦位置编码方式。
今天便以DETR模型为例,介绍正余弦编码的原理与实现过程。
首先给出其公式:
其中i指的是第几维度。

创建mask
这里的mask是DETR的骨干网络在对图像进行特征提取时为将所有图片统一到相同大小而采取填充方式生成的,主要是为了区别那块是填充的信息,这些信息在我们后面的注意力计算过程与位置编码过程中是不考虑的。
假设mask为4X4大小,输入图像大小为3X3。
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])#输入图像只是提供一个大小而已
a = torch.tensor(a)
下图为mask生成的4X4维度的矩阵,根据对应与输入图像大小3X3生成以下的mask编码tensor,下右图为反mask编码tensor,这一步就得到了图像的大小及对应与mask下的位置。
mask = [[False, False, False, True], [False, False, False, True], [False, False, False, True], [True, True, True, True]]
mask = torch.tensor(mask)
not_mask = ~mask

生成Y_embed和X_embed的tensor
y_embed = not_mask.cumsum(0, dtype=torch.float32)
x_embed = not_mask.cumsum(1, dtype=torch.float32)
DETR中运用两行编码实现Y_embed和X_embed,生成大小为(bitch_size , h , w)的tensor。这里认为batch-size=1即可。
根据反mask编码,生成的Y_embed和X_embed如下。
Y_embed对为mask编码True的进行行方向累加1,X_embed对为mask编码True的进行列方向累加1。下图所示:
运用10维(这个可以自行变化,代表的是你的要进行位置编码的维度)position进行编码,detr中设置为256。
num_pos_feats = 10
temperature = 10000
dim_t = torch.arange(num_pos_feats, dtype=torch.float32,device=a.device)#生成10维数,代表2i。
dim_t = temperature ** (2 * (dim_t // 2) / num_pos_feats) #i=dim_t // 2#对10维数进行计算
转换后的为:

生成pos_x以及pos_y
pos_x = x_embed[:, :, None] / dim_t
pos_y = y_embed[:, :, None] / dim_t
pos_x = torch.stack((pos_x[:, :, 0::2].sin(), pos_x[:, :, 1::2].cos()), dim=3).flatten(2)#不降维
pos_y = torch.stack((pos_y[:, :, 0::2].sin(), pos_y[:, :, 1::2].cos()), dim=3).flatten(2)#不降维


完成后直观效果如上图所示,可以对照第二步的X_embed和Y_embed,会发现pos_x,y的tensor分母和X,Y_embed对应 ,很好理解,其中i对应的是10维position的不同维度的数,d代表的是position编码维度。
组合Pos_x和Pos_y
因为上述位置编码的生成是行列方向分开的,这一步需要进行组合。
pos = torch.cat((pos_y, pos_x), dim=2)

组合以后直观图的样子如上,这时会发现16个位置的分母已经根据pos的不同,达到了位置编码的不同,因为本文采用的是10维的position,分子i的范围为0-10,每个位置就形成了1X20的tensor数据。文章来源:https://www.toymoban.com/news/detail-467315.html

上述两个位置的编码就可以理解为1X20的tensor数据,因为比较长,分开写了,不是4X5的,而是1X20的tensor数据,通过上图可以很直观的理解position encoding。
完整代码如下:文章来源地址https://www.toymoban.com/news/detail-467315.html
import torch
import numpy as np
import math
# 正余弦位置编码
num_pos_feats = 10
temperature = 10000
normalize = False
scale = 2 * math.pi#圆周率
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
a = torch.tensor(a)
mask = [[False, False, False, True], [False, False, False, True], [False, False, False, True], [True, True, True, True]]
mask = torch.tensor(mask)
print(mask)
assert mask is not None
not_mask = ~mask
print(not_mask)
y_embed = not_mask.cumsum(0, dtype=torch.float32)
x_embed = not_mask.cumsum(1, dtype=torch.float32)
print(y_embed)
print(x_embed)
if normalize:
eps = 1e-6
# b = a[i:j:s]表示:i,j与上面的一样,但s表示步进,缺省为1.
# 所以a[i:j:1]相当于a[i:j]
# 当s<0时,i缺省时,默认为-1. j缺省时,默认为-len(a)-1
# 所以a[::-1]相当于 a[-1:-len(a)-1:-1],也就是从最后一个元素到第一个元素复制一遍,即倒序。
# 对于X[:,:,m:n]是取三维矩阵中第m维到第n-1维的所有数据
# 归一化
y_embed = y_embed / (y_embed[-1:, :] + eps) * scale # y_embed[:, -1:, :]代表取三维数据中的最后一行数据
x_embed = x_embed / (x_embed[:, -1:] + eps) * scale # x_embed[:, :, -1:]代表取三维数据中的最后一列数据
print(y_embed)
print(x_embed)
dim_t1 = torch.arange(num_pos_feats, dtype=torch.float32, device=a.device)
print(dim_t1)
dim_t = temperature ** (2 * (dim_t1 // 2) / num_pos_feats) # i=dim_t1 // 2
print(dim_t)
pos_x = x_embed[:, :, None] / dim_t
pos_y = y_embed[:, :, None] / dim_t
print(pos_x)
print(pos_y)
pos_x = torch.stack((pos_x[:, :, 0::2].sin(), pos_x[:, :, 1::2].cos()), dim=3).flatten(2) # 不降维
pos_y = torch.stack((pos_y[:, :, 0::2].sin(), pos_y[:, :, 1::2].cos()), dim=3).flatten(2) # 不降维
print(pos_x)
print(pos_y)
pos = torch.cat((pos_y, pos_x), dim=2)
print(pos)
到了这里,关于Transformer正余弦位置编码理解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!