考研算法复试刷题19天：Prim算法求最小生成树【prim,最小生成树】-Toy模板网

这篇具有很好参考价值的文章主要介绍了考研算法复试刷题19天：Prim算法求最小生成树【prim,最小生成树】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

考研算法复试刷题19天：Prim算法求最小生成树【prim,最小生成树】

最小生成树

参考博客：图解：什么是最小生成树？ - 知乎 (zhihu.com)

总结下来的过程就是，一张图，我们将他化为树的形式，也就是生成树。那么最小生成树有是啥呢？所谓一个带权图的最小生成树，就是原图中边的权值最小的生成树，所谓最小是指边的权值之和小于或者等于其它生成树的边的权值之和。

如何操作才能生成最小生成树？

分为4步：

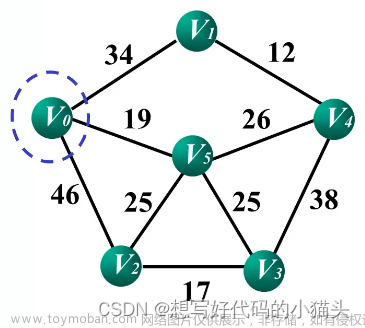
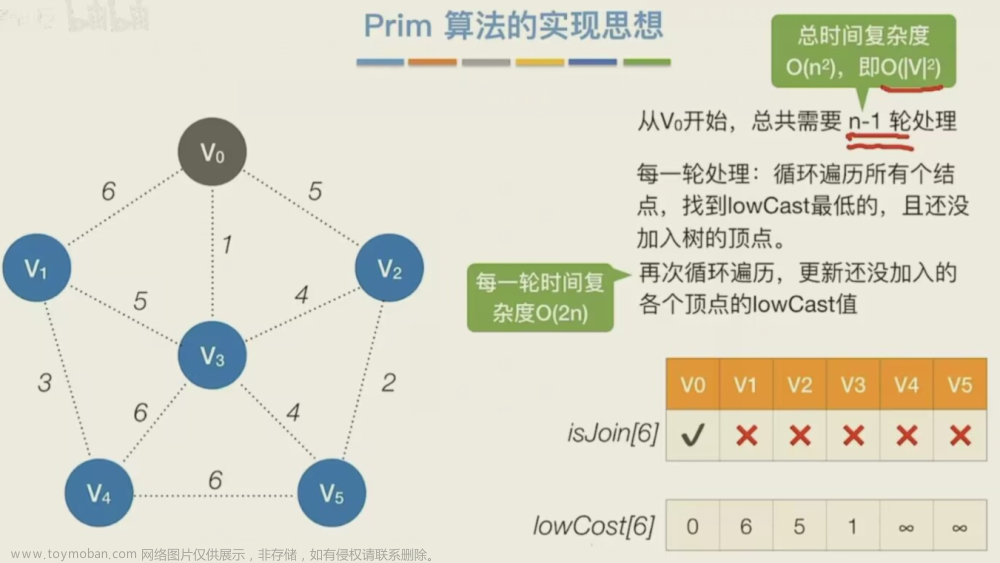
1. 一开始先随便找一个点(设为x)加入连通集，然后开始遍历其他图中的点

2. 找到离x最近的那个点并且和连通集有联系的点(第一次遍历就是图中和x有边的节点，如果是第n次的话，那么只要和连通集中任一节点有边即可)，然后将节点加入连通集。

3.然后更新现在还未加入连通集的节点离连通集的最小距离（因为连通集在第n次遍历之后，其包含的节点也是n个，所以说考量最短节点的时候是要重新算一遍，说的有点抽象，看图）。

考研算法复试刷题19天：Prim算法求最小生成树【prim,最小生成树】

4.重复上述3个步骤

为何这样操作就是最小

其实很简单，我们现在设连通集为T，现在有n个还未加入连通集的节点，其中有一个节点a离连通集只有1的距离，其他n-1个节点都离连通集的距离都大于1，此时我们要是不选择a的话，那么等到我们下一次将a选入的时候一定不会比现在选好，举个例子吧，假设一个节点为b，它离连通集的距离为2，然后它离a节点距离为1，我们现在先选b的话，那么带权路径之和res = res + b(2)；然后现在将a选入那么此时 res = res + b(2) + a(1)就增加了3，如果是先选a呢？其实很容易想出来，只增加了2，所以选a一定比选b好，那又有人问了，那万一b和a一样离连通集最近呢？我想说那样的话选谁都一样，选a不会比选b差。

题目详解

其实这道题就是模拟一下上述我写找最小生成树的过程。所以只要将思路理清楚了的话不难写出

1. 一开始先随便找一个点(设为x)加入连通集，然后开始遍历其他图中的点

//把一当成出发点
    dist[1] = 0;

for(int i=0;i<n;i++){
        int t = -1;
        //找到现在离连通集最近的点:
        //设置一个哨兵dist[t]，去和dist[j]中的每个值去比较
        //遍历途中只要小于哨兵的值就将哨兵的值更新成小的那个值
        //但是需要保证现在那个点没有在连通集中。
        for(int j=1;j<=n;j++){
            if(!vis[j]&&(t==-1||dist[t]>dist[j])){
                t = j;
            }
        }
        vis[t] = true;
        if(dist[t]==INF) return INF;
        
        // cout<<"t:"<<t<<"dist[t]:"<<dist[t]<<endl;
        res += dist[t];
}

3.然后更新现在还未加入连通集的节点离连通集的最小距离

for(int j=1;j<=n;j++){
            // cout<<"t:"<<t<<"g[t][j]:"<<g[t][j]<<" ";
            dist[j] = min(dist[j],g[t][j]); 
        }

这样就可以将prim总的代码写出（很重要，需要理解并记住）文章来源地址https://www.toymoban.com/news/detail-467699.html

int Prim(){
    int res = 0;
    memset(dist,0x3f,sizeof(dist));
    //把一当成出发点
    dist[1] = 0;
    for(int i=0;i<n;i++){
        int t = -1;
        //找到现在离连通集最近的点:
        //设置一个哨兵dist[t]，去和dist[j]中的每个值去比较
        //遍历途中只要小于哨兵的值就将哨兵的值更新成小的那个值
        //但是需要保证现在那个点没有在连通集中。
        for(int j=1;j<=n;j++){
            if(!vis[j]&&(t==-1||dist[t]>dist[j])){
                t = j;
            }
        }
        vis[t] = true;
        if(dist[t]==INF) return INF;
        
        // cout<<"t:"<<t<<"dist[t]:"<<dist[t]<<endl;
        res += dist[t];
        for(int j=1;j<=n;j++){
            // cout<<"t:"<<t<<"g[t][j]:"<<g[t][j]<<" ";
            dist[j] = min(dist[j],g[t][j]); 
        }
        // cout<<endl;
    }
    return res;
}

AC代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int INF = 0x3f3f3f3f;
//存图的连接关系和权重
int g[510][510];
//
int dist[510];
bool vis[510];
int n,m;

int Prim(){
    int res = 0;
    memset(dist,0x3f,sizeof(dist));
    //把一当成出发点
    dist[1] = 0;
    for(int i=0;i<n;i++){
        int t = -1;
        //找到现在离连通集最近的点:
        //设置一个哨兵dist[t]，去和dist[j]中的每个值去比较
        //遍历途中只要小于哨兵的值就将哨兵的值更新成小的那个值
        //但是需要保证现在那个点没有在连通集中。
        for(int j=1;j<=n;j++){
            if(!vis[j]&&(t==-1||dist[t]>dist[j])){
                t = j;
            }
        }
        vis[t] = true;
        if(dist[t]==INF) return INF;
        
        // cout<<"t:"<<t<<"dist[t]:"<<dist[t]<<endl;
        res += dist[t];
        for(int j=1;j<=n;j++){
            // cout<<"t:"<<t<<"g[t][j]:"<<g[t][j]<<" ";
            dist[j] = min(dist[j],g[t][j]); 
        }
        // cout<<endl;
    }
    return res;
}

int main(){
    cin>>n>>m;
    //memset 英文:设置
    memset(g,0x3f,sizeof(g));
    while(m--){
        int a,b,c;
        cin>>a>>b>>c;
        //这一步不是很理解，等会测试一下
        g[a][b] = g[b][a] = min(c,g[a][b]);
        // cout<<g[a][b]<<endl;
    }
    int res = Prim();
    if(res == INF){
        cout<<"impossible";
    }else{
        cout<<res;
    }
    return 0;
}

到了这里，关于考研算法复试刷题19天：Prim算法求最小生成树【prim,最小生成树】的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！