活动地址：CSDN21天学习挑战赛
👨🎓作者简介：一位喜欢写作，计科专业大三菜鸟🏡个人主页：starry陆离
🕒首发日期：2022年8月16日星期二
🌌上期文章：『动态规划』动态规划概述
📚订阅专栏：『算法分析与设计』
如果文章有帮到你的话记得点赞👍+收藏💗支持一下哦
1.完全加括号的矩阵连乘积
完全加括号的矩阵连乘积可递归地定义为：
- 单个矩阵是完全加括号的
- 矩阵连乘积A是完全加括号的，则A可表示为2个完全加括号的矩阵连乘积B和C 的乘积并加括号，即A=(BC)
设有四个矩阵A, B, C, D ，它们的维数分别是：
A = 50*10 B = 10*40 C = 40*30 D = 30*5
总共有五种完全加括号的方式：
2.矩阵连乘问题
-
给定n个矩阵{A1,A2,…,An}，其中Ai和Ai+1是可乘的，i=1,2,…,n-1
-
考察n个矩阵的连乘积
A1 A2 … An
-
矩阵乘法满足结合律->计算矩阵的连乘可以有许多不同的计算次序->计算次 序可以用加括号的方式来确定
-
若一个矩阵连乘积的计算次序完全确定（该连乘积已完全加括号）->可依此 次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积
问？？ 如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的 数乘次数最少
2.2穷举法
列举出所有可能的计算次序，并计算出每一种计算次序相应需要的数乘 次数，从中找出一种数乘次数最少的计算次序
算法复杂度分析： 对于n个矩阵的连乘积，设其不同的计算次序为P(n)。 由于每种加括号方式都可以分解为两个子矩阵的加括号问题：
(A1 ...Ak )(Ak+1…An )可以得到关于P(n)的递推式如下：
2.3动态规划
2.3.1问题分析
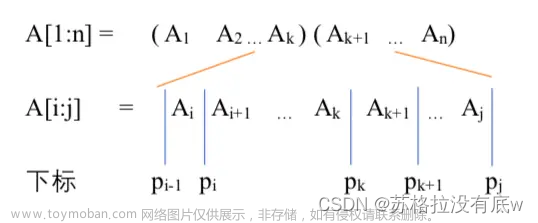
将矩阵连乘积 AiAi+1......Aj，简记为A[i:j],i≤j
考察计算A[i:j]的最优计算次序：设这个计算次序在矩阵Ak和Ak+1之间将矩阵 链断开，i≤k<j,则其相应完全加括号方式为
计算量：A[i:k]的计算量加上A[k+1:j]的计算量，再加上A[i:k]和A[k+1:j]相 乘的计算量（三部分组成）
2.3.2分析最优解的结构
特征：计算A[i:j]的最优次序所包含的计算矩阵子链A[i:k]和A[k+1:j]的次序也是也是最优的
矩阵连乘计算次序问题的最优解包含着其子问题的最优解->因此具备最优子结构
2.3.3建立递归关系
计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为 m[1,n]
- 当
i=j时，A[i:j]=Ai，因此，m[i,i]=0，i=1,2,…,n - 当
i<j时，m[i,j]=m[i,k]+m[k+1,j]+ Pi-1 · Pk · Pj
Ai的维数为Pi-1 · Pi
可以递归地定义m[i,j]为：
2.3.4计算最优值
对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问题。不同子问题的个数最多只 有：O(n^2)
在递归计算时，许多子问题被重复计算多次->重叠子问题
- 用动态规划算法解此问题，可依据其递归式以自底向上的方式进行计算，在计算过程中，保存已解决的子问题答案
- 每个子问题只计算一次，而在后面需要时只要简单查一下，从而避免大量的重 复计算，最终得到多项式时间的算法
文章来源：https://www.toymoban.com/news/detail-467753.html
2.3.5用动态规划求解最优解
文章来源地址https://www.toymoban.com/news/detail-467753.html
3.算法实现
3.1备忘录法
/*
int n;//输入的数的个数
int[] num;//储存数
int[][] m;//动态规划数组，保存当前最优解
int[][] s;//用于构造最优解
*/
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int n;
int[] num;
int[][] m;
int[][] s;
while(scanner.hasNext()) {
n=scanner.nextInt();
num=new int[n];
m=new int[n][n];
p=new int[n];
s=new int[n][n];
for(int i=0;i<n;++i) {
num[i]=scanner.nextInt();
}
int ans=Solve(1,n-1,m,num,s);
System.out.println(ans);
}
}
private static int Solve(int i, int j,int[][] m,int[] num,int[][] s) {
if(m[i][j]>0)return m[i][j];
if(i==j)return 0;
int u=Solve(i+1, j, m,num,s)+num[i-1]*num[i]*num[j];
s[i][j]=i;
for(int k=i+1;k<j;++k) {
int t=Solve(i, k, m, num, s)+Solve(k+1, j, m, num, s)+num[i-1]*num[k]*num[j];
if(t<u) {
u=t;s[i][j]=k;
}
m[i][j]=u;
}
return u;
}
}
3.2动态规划
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int n;
int[] num;
int[][] m;
int[][] s;
while(scanner.hasNext()) {
n=scanner.nextInt();
num=new int[n+1];
m=new int[n+1][n+1];
s=new int[n+1][n+1];
for(int i=0;i<n;++i) {
num[i]=scanner.nextInt();
}
n=n-1;
for(int i=1;i<=n;++i) {m[i][i]=0;}
for(int r=2;r<=n;r++) {
for(int i=1;i<=n-r+1;i++) {
int j=i+r-1;
m[i][j]=m[i+1][j]+num[i-1]*num[i]*num[j];
s[i][j]=i;
for(int k=i+1;k<j;k++) {
int t=m[i][k]+m[k+1][j]+num[i-1]*num[k]*num[j];
if(t<m[i][j]) {
m[i][j]=t;
s[i][j]=k;
}
}
}
}
traceback(s,1,n);
//System.out.println(m[1][n]);
}
}
private static void traceback(int[][] s, int i, int j) {
if(i==j)return;
traceback(s, i, s[i][j]);
traceback(s, s[i][j]+1, j);
System.out.println("A["+i+":"+s[i][j]+"] * A["+(s[i][j]+1)+":"+j+"]");
}
}
到了这里，关于『动态规划』矩阵连乘的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
