Matlab多元非线性函数拟合-Toy模板网

这篇具有很好参考价值的文章主要介绍了Matlab多元非线性函数拟合。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

看了多篇文章，觉得没有一篇比较全，且可以参照的多元非线性函数拟合，看了多篇文章后总结以下内容，主要以示例给出，希望能帮助到大家快速上手。

1.需要用到的函数语法

beta = nlinfit(X, Y, modelfun, beta0) X为你的自变量，Y是因变量，modelfun是你用inline定义的函数名字，beta0是模型参数的初始值。
还有一个inline的语法，用于定义函数句柄，请参照下面看具体的用法。

2. 多元拟合概述

1.当你需要拟合一个多元函数的时候，需要首先知道其大致的模型，即参数待定的模型，如， $y=b_0+b_1*x_1+b_2*x_2+b_3*x_3$ 那么就可以用定义一个函数

mymodel =inline( 'b(1) + b(2) .* x(:,1) + b(3) .* x(:,2) + b(4) .* x(:,3)' ,'b','x');

虽然我给出的的线性函数，但非线性函数也是一样的只需要在inlien里面定义好就行。

2.接下来需要原始数据，这里我的例子会给出数据，方便参照，其次你需要设置初始的参数值如代码中的beta0;
给出拟合例子如下：

clc;clear;close all;
x(:,1) = [180	201	205	208	213	217	218	222	226	230	233	238	240	242	253]';  % 跳高成绩
x(:,2)= [280 240 226 224 220 217 225 221 211 213 199 198 195 186 183]';    % 1000m成绩
x(:,3)= [153 170 162 160 162 165 170 168 169 179 172 172 175 181 176]';    % 跳绳个数
Y = [60	75 70 70 75	75 85 80 80	85 90 90 90	95 95]';                    % 综合打分

mymodel =inline( 'b(1) + b(2) .* x(:,1) + b(3) .* x(:,2) + b(4) .* x(:,3)' ,'b','x');
beta0=[9.5,0.7,0.29,0.88];
y0=beta0(1)+beta0(2)* x(:,1)+ beta0(3) .* x(:,2) + beta0(4) .* x(:,3);
beta=nlinfit(x,Y,mymodel,beta0);
yn=beta(1)+beta(2)* x(:,1)+ beta(3) .* x(:,2) + beta(4) .* x(:,3);
 plot(yn,'DisplayName','yn');hold on;plot(y0,'DisplayName','y0');hold off;
  legend('\fontname{宋体}拟合参数后的曲线','\fontname{宋体}初始参数下的曲线');

可以得到如下的拟合曲线图，
![在这里插入图片描述](https://img-blog.csdnimg.cn/f291769b96124993b3b135b894a52bfd.png Matlab多元非线性函数拟合

3 一元函数拟合验证

其实这种方法也可以用于一元线性回归，代码简单。给出例子如下。

X = 1 : 10;
Y = [0 4 8 17 29 34 54 62 80 99];
mymodel = inline('beta(1) * X .^ beta(2)', 'beta', 'X');
beta0 = [1, 2];
beta = nlinfit(X, Y, mymodel, beta0);
yy=beta(1)*X.^beta(2);
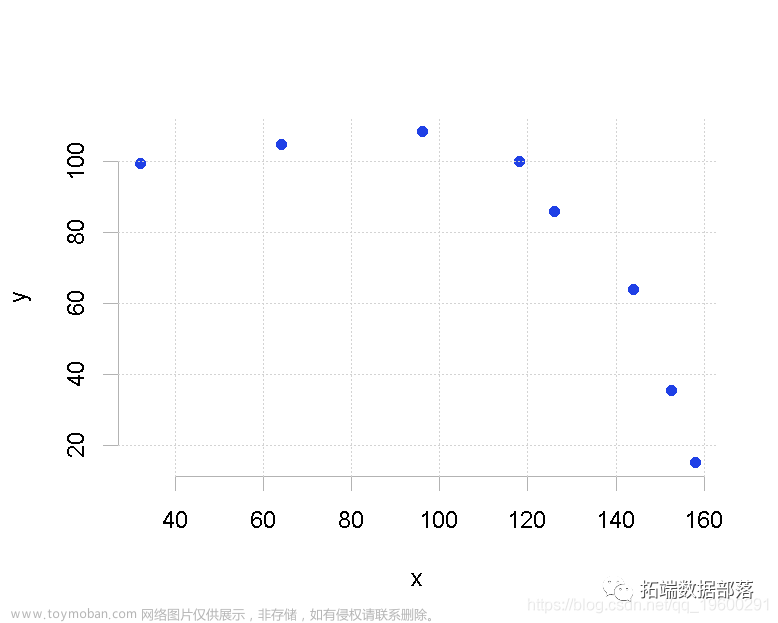
plot(X,Y,'*',X,yy,'-or');