文档总目录
英文原文(Linear algebra and decomposition)
本节说明如何求解线性系统,计算各种分解,如 LU、QR、SVD、特征分解……
求解基本线性系统
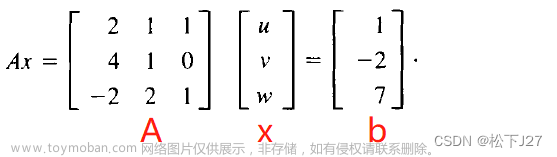
问题:有一个方程组,写成矩阵方程如下:
A
x
=
b
Ax = b
Ax=b
其中
A
A
A 和
b
b
b 是矩阵(作为一种特殊情况,
b
b
b 也可以是一个向量)。求解
x
x
x。
解:可以根据矩阵 A A A 的属性以及效率和准确性,在各种分解之间进行选择。如下是一个很好的折衷方案:
// 代码索引 4-1-1-1
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::Matrix3f A;
Eigen::Vector3f b;
A << 1,2,3, 4,5,6, 7,8,10;
b << 3, 3, 4;
std::cout << "Here is the matrix A:\n" << A << std::endl;
std::cout << "Here is the vector b:\n" << b << std::endl;
Eigen::Vector3f x = A.colPivHouseholderQr().solve(b);
std::cout << "The solution is:\n" << x << std::endl;
}
输出如下:
Here is the matrix A:
1 2 3
4 5 6
7 8 10
Here is the vector b:
3
3
4
The solution is:
-2
1
1
在此示例中,colPivHouseholderQr() 方法返回类 ColPivHouseholderQR 的对象。由于这里的矩阵是 Matrix3f 类型,所以这一行可以替换为:
ColPivHouseholderQR<Matrix3f> dec(A);
Vector3f x = dec.solve(b);
在这里,ColPivHouseholderQR 是列主元 QR 分解。这是本教程的一个很好的折衷方案,因为它适用于所有矩阵,而且速度非常快。
以下是可以选择的其他一些分解表,具体取决于矩阵、解决的问题以及需求:
| 描述 | 方法 | 对矩阵的要求 | 速度(中小矩阵) | 速度(大矩阵) | 精度 |
|---|---|---|---|---|---|
| PartialPivLU | partialPivLu() | Invertible(可逆) | ++ | ++ | + |
| FullPivLU | fullPivLu() | None | - | - - | +++ |
| HouseholderQR | householderQr() | None | ++ | ++ | + |
| ColPivHouseholderQR | colPivHouseholderQr() | None | + | - | +++ |
| FullPivHouseholderQR | fullPivHouseholderQr() | None | - | - - | +++ |
| CompleteOrthogonalDecomposition | completeOrthogonalDecomposition() | None | + | - | +++ |
| LLT | llt() | Positive definite(正定) | +++ | +++ | + |
| LDLT | ldlt() | Positive or negative semidefinite(半正定或半负定) | +++ | + | ++ |
| BDCSVD | bdcSvd() | None | - | - | +++ |
| JacobiSVD | jacobiSvd() | None | - | - - - | +++ |
要大致了解不同分解的真实相对速度,请查看基准测试。
所有这些分解都提供了一个 solve() 方法,其工作方式与上例相同。
可以根据矩阵的属性来选择相应的方法。例如,要求解具有非对称满秩矩阵的线性系统,可以使用 PartialPivLU。如果知道矩阵是对称和正定的,可以选择 LLT 或 LDLT 分解。
示例如下:
// 代码索引 4-1-2-1
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::Matrix2f A, b;
A << 2, -1, -1, 3;
b << 1, 2, 3, 1;
std::cout << "Here is the matrix A:\n" << A << std::endl;
std::cout << "Here is the right hand side b:\n" << b << std::endl;
Eigen::Matrix2f x = A.ldlt().solve(b);
std::cout << "The solution is:\n" << x << std::endl;
}
输出为:
Here is the matrix A:
2 -1
-1 3
Here is the right hand side b:
1 2
3 1
The solution is:
1.2 1.4
1.4 0.8
有关 Eigen 支持的所有分解的更完整的表格( Eigen 还支持许多其他分解),请参阅[下一节](#4.2 稠密分解目录)。
最小二乘求解
在最小二乘意义上解决欠定或超定线性系统的最普遍和准确的方法是 SVD 分解。Eigen 提供了两种实现。推荐的是 BDCSVD 类,它可以很好地处理大型矩阵问题,并自动回退到 JacobiSVD 类以处理较小矩阵的问题。对于这两个类,他们的 solve() 方法在最小二乘意义上解决了线性系统。
示例如下:
// 代码索引 4-1-3-1
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::MatrixXf A = Eigen::MatrixXf::Random(3, 2);
std::cout << "Here is the matrix A:\n" << A << std::endl;
Eigen::VectorXf b = Eigen::VectorXf::Random(3);
std::cout << "Here is the right hand side b:\n" << b << std::endl;
std::cout << "The least-squares solution is:\n"
<< A.bdcSvd(Eigen::ComputeThinU | Eigen::ComputeThinV).solve(b) << std::endl;
}
输出:
Here is the matrix A:
0.68 0.597
-0.211 0.823
0.566 -0.605
Here is the right hand side b:
-0.33
0.536
-0.444
The least-squares solution is:
-0.67
0.314
SVD 的替代方法是 CompleteOrthogonalDecomposition,它通常速度更快且准确度差不多。
同样,如果对问题了解更多,可以更好的可能更快的方法。如果矩阵是满秩的,HouseHolderQR 是首选方法。如果矩阵是满秩且是良态的,则在正规方程的矩阵上使用 Cholesky 分解 (LLT) 可能会更快。关于最小二乘求解的更多详细信息,请参见 求解线性最小二乘系统。
检查矩阵是否为奇异矩阵
Eigen 允许根据具体的误差自己进行此计算,如本例所示:
// 代码索引 4-1-4-1
#include <iostream>
#include <Eigen/Dense>
using Eigen::MatrixXd;
int main()
{
MatrixXd A = MatrixXd::Random(100,100);
MatrixXd b = MatrixXd::Random(100,50);
MatrixXd x = A.fullPivLu().solve(b);
double relative_error = (A*x - b).norm() / b.norm(); // norm() is L2 norm
std::cout << "The relative error is:\n" << relative_error << std::endl;
}
输出:
The relative error is:
2.31495e-14
计算特征值和特征向量
这里需要使用一个特征分解,以检查矩阵是否自伴。如下示例使用 SelfAdjointEigenSolver ,它可以很容易地处理使用 EigenSolver 或 ComplexEigenSolver 的 的一般矩阵。
特征值和特征向量的计算不一定收敛,但这种不收敛的情况很少见。可以调用 info() 检查这种可能性。
// 代码索引 4-1-5-1
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::Matrix2f A;
A << 1, 2, 2, 3;
std::cout << "Here is the matrix A:\n" << A << std::endl;
Eigen::SelfAdjointEigenSolver<Eigen::Matrix2f> eigensolver(A);
if (eigensolver.info() != Eigen::Success) abort();
std::cout << "The eigenvalues of A are:\n" << eigensolver.eigenvalues() << std::endl;
std::cout << "Here's a matrix whose columns are eigenvectors of A \n"
<< "corresponding to these eigenvalues:\n"
<< eigensolver.eigenvectors() << std::endl;
}
输出如下:
Here is the matrix A:
1 2
2 3
The eigenvalues of A are:
-0.236
4.24
Here's a matrix whose columns are eigenvectors of A
corresponding to these eigenvalues:
-0.851 -0.526
0.526 -0.851
计算逆和行列式
虽然逆和行列式是基本的数学概念,但在数值线性代数中它们不如在纯数学中有用。逆计算通常被 solve() 操作有利地取代,行列式通常不是检查矩阵是否可逆的好方法。
但是,对于非常小的矩阵,上述情况可能并非如此,逆矩阵和行列式可能非常有用。
虽然某些分解(例如 PartialPivLU 和 FullPivLU)提供了 inverse() 和 determinant() 方法,但也可以直接在矩阵上调用inverse() 和 determinant()。如果矩阵是非常小的固定大小(最多 4x4),这种方法可以让 Eigen 不执行 LU 分解,以提高效率。
示例如下:
// 代码索引 4-1-6-1
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::Matrix3f A;
A << 1, 2, 1,
2, 1, 0,
-1, 1, 2;
std::cout << "Here is the matrix A:\n" << A << std::endl;
std::cout << "The determinant of A is " << A.determinant() << std::endl;
std::cout << "The inverse of A is:\n" << A.inverse() << std::endl;
}
输出:
Here is the matrix A:
1 2 1
2 1 0
-1 1 2
The determinant of A is -3
The inverse of A is:
-0.667 1 0.333
1.33 -1 -0.667
-1 1 1
将计算与构造分开
在上面的示例中,分解操作是在构造分解对象的同时计算的。然而,在某些情况下,可能希望将这两件事分开,例如,如果在构造时不知道要分解的矩阵,或者想重用现有的分解对象。
实现方法如下:
- 所有分解都有一个默认构造函数。
- 所有分解都有一个
compute(matrix)方法来进行计算,并且可以在已经计算的分解上再次调用它,重新初始化它。
示例如下:
// 代码索引 4-1-7-1
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::Matrix2f A, b;
Eigen::LLT<Eigen::Matrix2f> llt;
A << 2, -1, -1, 3;
b << 1, 2, 3, 1;
std::cout << "Here is the matrix A:\n" << A << std::endl;
std::cout << "Here is the right hand side b:\n" << b << std::endl;
std::cout << "Computing LLT decomposition..." << std::endl;
llt.compute(A);
std::cout << "The solution is:\n" << llt.solve(b) << std::endl;
A(1,1)++;
std::cout << "The matrix A is now:\n" << A << std::endl;
std::cout << "Computing LLT decomposition..." << std::endl;
llt.compute(A);
std::cout << "The solution is now:\n" << llt.solve(b) << std::endl;
}
输出:
Here is the matrix A:
2 -1
-1 3
Here is the right hand side b:
1 2
3 1
Computing LLT decomposition...
The solution is:
1.2 1.4
1.4 0.8
The matrix A is now:
2 -1
-1 4
Computing LLT decomposition...
The solution is now:
1 1.29
1 0.571
最后,可以告诉分解构造函数为给定大小的分解矩阵预先分配存储空间,这样当随后分解这些矩阵时,就不会进行动态内存分配(当然,如果使用的是固定大小的矩阵,则不会进行动态内存分配)。
这是通过将大小传递给分解构造函数来完成的,示例如下:
HouseholderQR<MatrixXf> qr(50,50);
MatrixXf A = MatrixXf::Random(50,50);
qr.compute(A); // no dynamic memory allocation
可以计算秩的分解
某些分解能够计算矩阵的秩,这些通常也是在处理非满秩矩阵时表现最好的分解(在正方形情况下表示奇异矩阵)。关于分解是否可以计算矩阵的秩,请参阅下一节。
可以计算秩的分解至少提供了一个 rank() 方法。还有更简单的方法,例如 isInvertible(),有些还提供计算矩阵的核(零空间)和图像(列空间)的方法,例如 FullPivLU:
// 代码索引 4-1-8-1
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::Matrix3f A;
A << 1, 2, 5,
2, 1, 4,
3, 0, 3;
std::cout << "Here is the matrix A:\n" << A << std::endl;
Eigen::FullPivLU<Eigen::Matrix3f> lu_decomp(A);
std::cout << "The rank of A is " << lu_decomp.rank() << std::endl;
std::cout << "Here is a matrix whose columns form a basis of the null-space of A:\n"
<< lu_decomp.kernel() << std::endl;
std::cout << "Here is a matrix whose columns form a basis of the column-space of A:\n"
<< lu_decomp.image(A) << std::endl; // yes, have to pass the original A
}
输出:
Here is the matrix A:
1 2 5
2 1 4
3 0 3
The rank of A is 2
Here is a matrix whose columns form a basis of the null-space of A:
0.5
1
-0.5
Here is a matrix whose columns form a basis of the column-space of A:
5 1
4 2
3 3
当然,任何秩计算都取决于阈值的选择,因为实际上没有任何浮点矩阵是秩亏的。Eigen 根据不同分解选择一个合理的默认阈值,但通常是对角线大小乘以机器浮点精度。虽然这是 Eigen 可以选择的最佳默认值,但只有用户知道应用程序的正确阈值是多少。用户可以通过在调用 rank() 或其他需要使用此类阈值的方法之前对分解对象调用 setThreshold() 来设置自定义阈值。分解本身,即 compute() 方法,与阈值无关。更改阈值后无需重新计算分解。文章来源:https://www.toymoban.com/news/detail-468004.html
// 代码索引 4-1-8-2
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::Matrix2d A;
A << 2, 1,
2, 0.9999999999;
Eigen::FullPivLU<Eigen::Matrix2d> lu(A);
std::cout << "By default, the rank of A is found to be " << lu.rank() << std::endl;
lu.setThreshold(1e-5);
std::cout << "With threshold 1e-5, the rank of A is found to be " << lu.rank() << std::endl;
}
输出:文章来源地址https://www.toymoban.com/news/detail-468004.html
By default, the rank of A is found to be 2
With threshold 1e-5, the rank of A is found to be 1
到了这里,关于[Eigen中文文档] 线性代数与分解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!


![信号与系统的一些基本问题之信号分解完备正交基[1]—线性代数向量空间与向量基的基础](https://imgs.yssmx.com/Uploads/2024/04/858588-1.png)




