💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
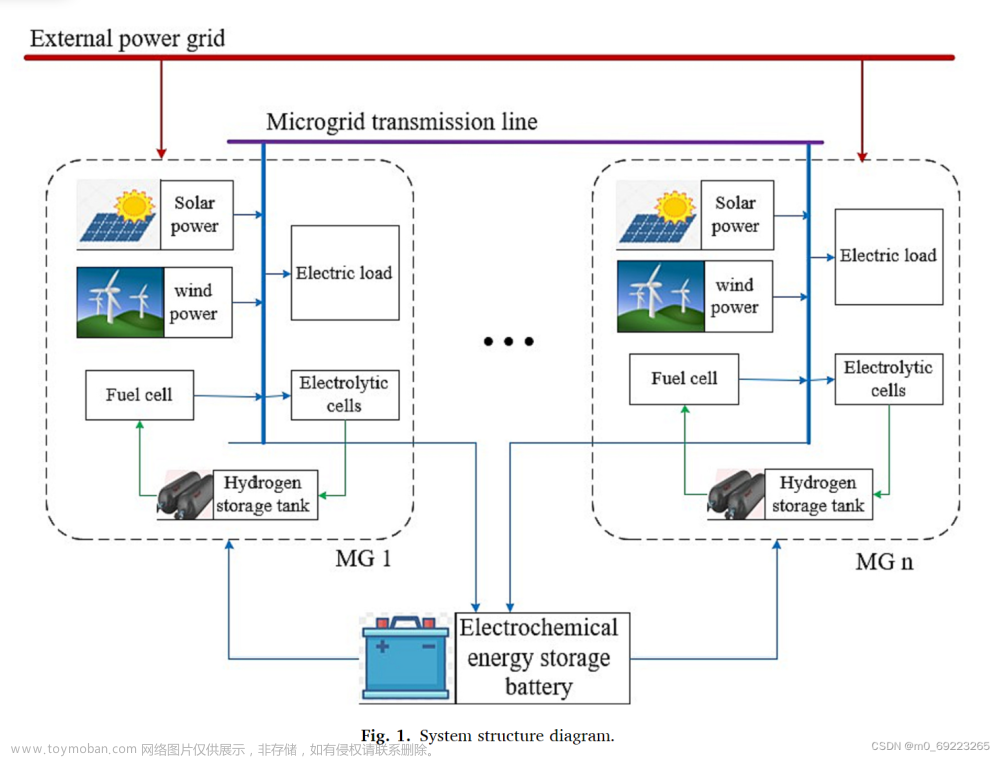
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码、数据、文章讲解
💥1 概述
文献来源:
 文章来源地址https://www.toymoban.com/news/detail-468719.html
文章来源地址https://www.toymoban.com/news/detail-468719.html
摘要:非负矩阵分解 (NMF) 是一种线性降维 分析非负数据的技术。NMF 的一个关键方面是选择 依赖于噪声模型(或 噪声)假设数据。在许多应用中,噪声模型是未知的 而且难以估计。在本文中,我们定义了一个多目标NMF (MO-NMF) 问题,其中多个目标在同一 NMF 中组合 型。我们建议使用拉格朗日对偶性来明智地优化一组 在加权和法框架内使用的加权,即 我们最小化单个目标函数,它是 all 的加权和 目标函数。我们设计了一种基于乘法的简单算法 更新以最小化此加权总和。我们展示了如何使用它来查找 分布稳健的 NMF (DR-NMF) 解决方案,即 最小化所有目标中的最大误差,使用双重方法解决 通过受弗兰克-沃尔夫算法启发的启发式方法。我们说明 这种方法对合成、文档和音频数据集的有效性。这 结果表明,DR-NMF对噪声模型的识别具有鲁棒性 NMF问题。
原文摘要:
Abstract: Nonnegative matrix factorization (NMF) is a linear dimensionality reduction technique for analyzing nonnegative data. A key aspect of NMF is the choice of the objective function that depends on the noise model (or statistics of the noise) assumed on the data. In many applications, the noise model is unknown and difficult to estimate. In this paper, we define a multi-objective NMF (MO-NMF) problem, where several objectives are combined within the same NMF model. We propose to use Lagrange duality to judiciously optimize for a set of weights to be used within the framework of the weighted-sum approach, that is, we minimize a single objective function which is a weighted sum of the all objective functions. We design a simple algorithm based on multiplicative updates to minimize this weighted sum. We show how this can be used to find distributionally robust NMF (DR-NMF) solutions, that is, solutions that minimize the largest error among all objectives, using a dual approach solved via a heuristic inspired from the Frank-Wolfe algorithm. We illustrate the effectiveness of this approach on synthetic, document and audio data sets. The results show that DR-NMF is robust to our incognizance of the noise model of the NMF problem.



📚2 运行结果
% DR-NMF
options.scalings = [1/solall{1}(1,end); 1/solall{end}(2,end)];
x = x*options.scalings(1);
y = y*options.scalings(2);
options.distribrobust = 1;
options.lambda = [0.5;0.5];
fprintf('Computing the solution of DR-NMF. \n');
[Wr,Hr,er,lam] = multiNMFbeta(X,r,options);% Plot Pareto Front
set(0, 'DefaultAxesFontSize', 12);
set(0, 'DefaultLineLineWidth', 2);
figure;
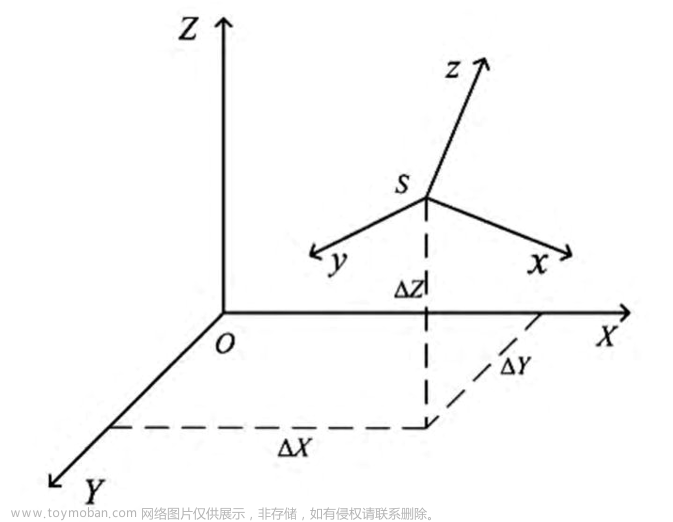
plot(x,y,'o--'); hold on;
plot(er(1,end),er(2,end),'kx','MarkerSize',12);
maxxy = min(max(x), max(y));
plot([1 maxxy],[1 maxxy],'k--');
xlabel('First objective');
ylabel('Second objective');
legend('Pareto Front', 'DR-NMF', 'x = y');title(sprintf('Pareto frontier for a randomly generated matrix: \n IS-NMF vs. KL-NMF, and DR-NMF'));

load('piano_Mary.mat');
[m,n] = size(V);
r = 4;
% Initialization & parameters
options.W = rand(m,r);
options.H = rand(r,n);
options.beta = [0;1];
options.distribrobust = 0;
options.maxiter = 100;
% IS-NMF
options.lambda = [1; 0];
fprintf('Computing the solution of NMF with Itakuro-Saito (IS-NMF) divergence: \n');
[Wis,His,eis] = multiNMFbeta(V,r,options);
% KL-NMF
options.lambda = [0; 1];
fprintf('Computing the solution of with Kullback-Leibler (KL-NMF) divergence: \n');
[Wkl,Hkl,ekl] = multiNMFbeta(V,r,options);
% DR-NMF
% This is crucial: you need to specify the scaling of the objective
% functions; cf. the paper.
options.scalings = [1/eis(1,end); 1/ekl(2,end)];
options.distribrobust = 1;
fprintf('Computing the solution of distributionally robust NMF (DR-NMF): \n');
[Wdr,Hdr,edr,lam] = multiNMFbeta(V,r,options);% Display errors
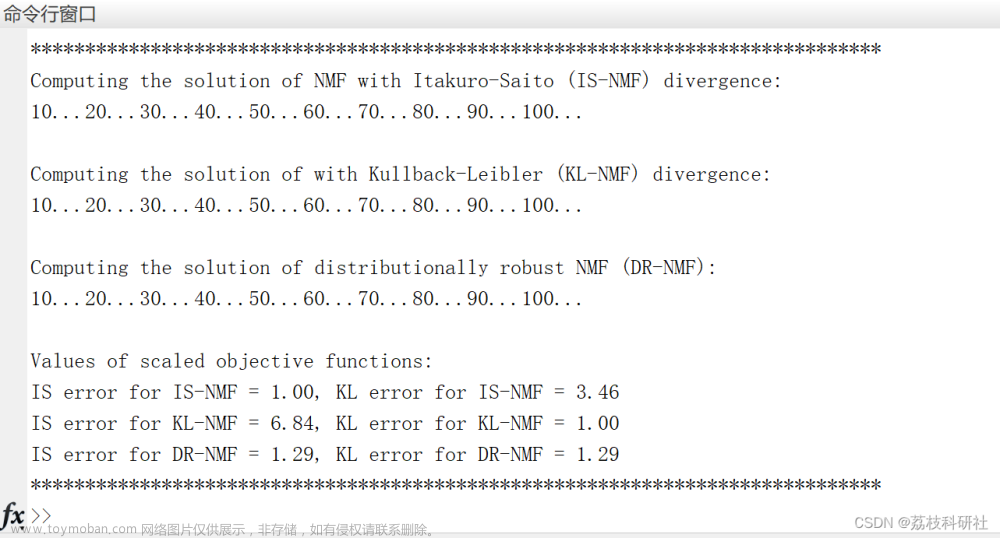
display('Values of scaled objective functions:');
fprintf('IS error for IS-NMF = %2.2f, KL error for IS-NMF = %2.2f\n', 1,eis(2,end)/ekl(2,end));
fprintf('IS error for KL-NMF = %2.2f, KL error for KL-NMF = %2.2f\n', ekl(1,end)/eis(1,end),1);
fprintf('IS error for DR-NMF = %2.2f, KL error for DR-NMF = %2.2f\n', edr(1,end),edr(2,end));
fprintf('******************************************************************************\n')% Plot errors
% Display
set(0, 'DefaultAxesFontSize', 9);
set(0, 'DefaultLineLineWidth', 2);
figure;
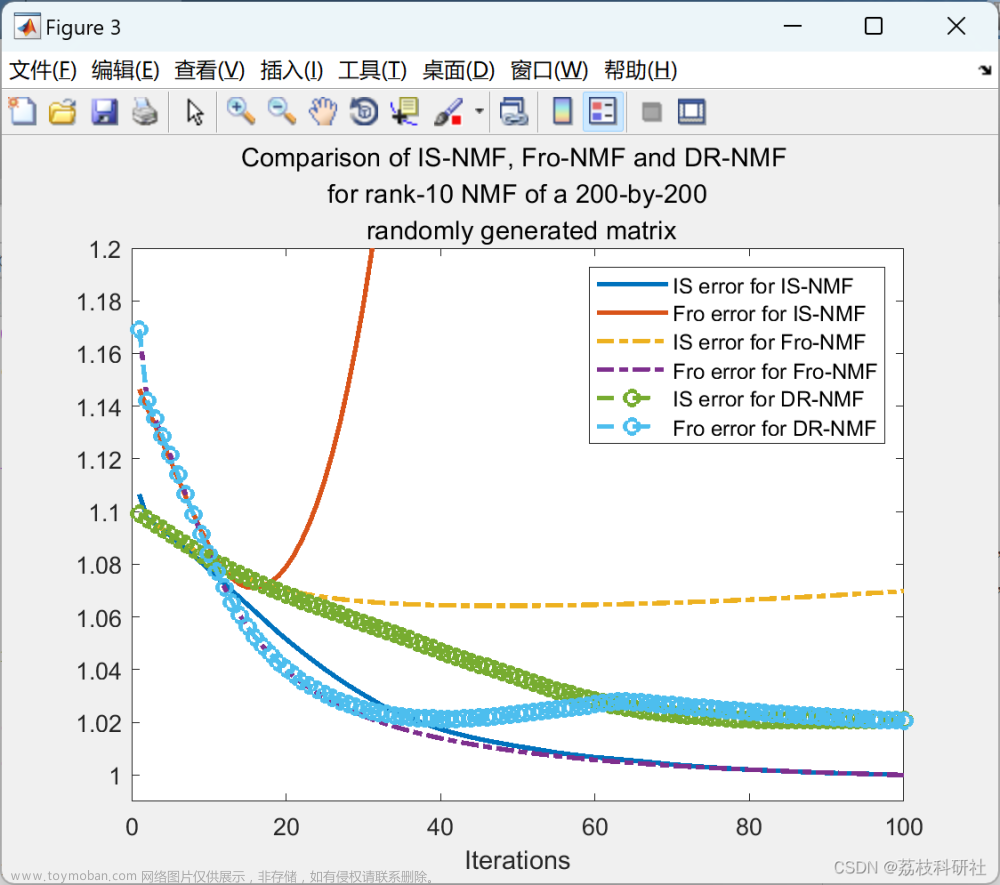
plot( (eis.*repmat(options.scalings,1,size(eis,2)))' ); hold on;
plot( (ekl.*repmat(options.scalings,1,size(ekl,2)))','-.');
plot( edr' ,'o--');
legend('IS error for IS-NMF', 'KL error for IS-NMF', ...
'IS error for KL-NMF', 'KL error for KL-NMF', ...
'IS error for DR-NMF', 'KL error for DR-NMF');
axis([0 100 0.95 10]);
xlabel('Iterations');
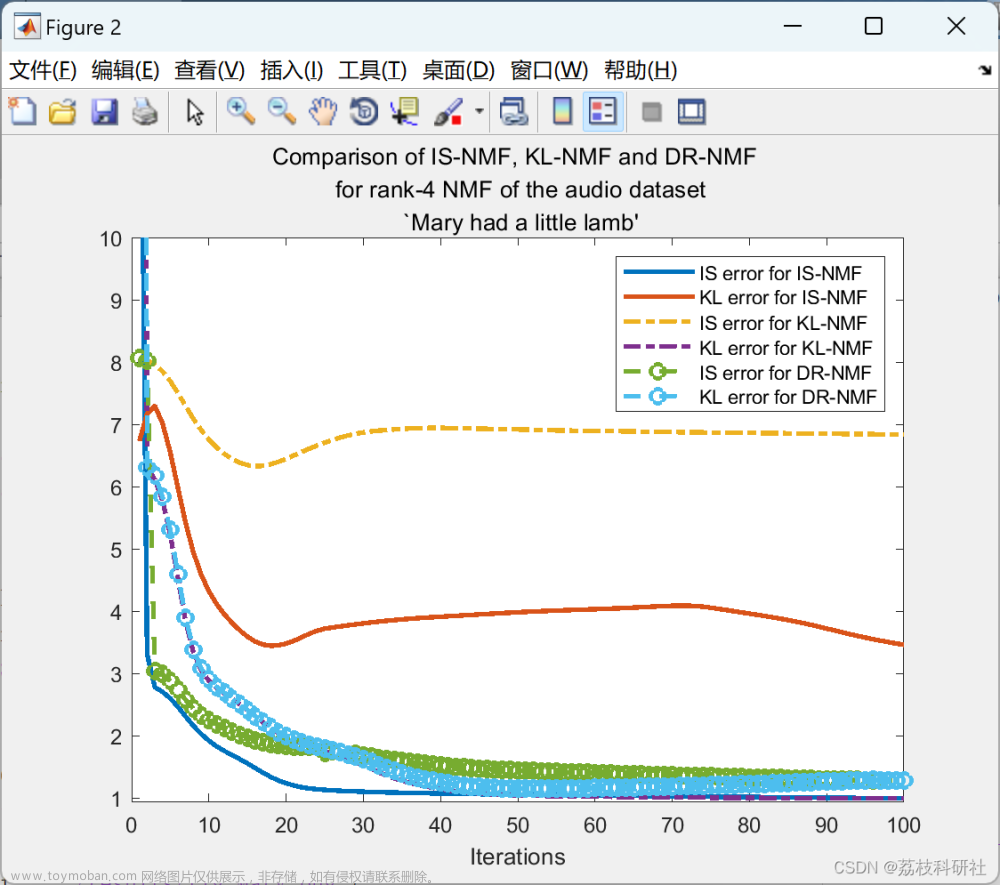
title(sprintf('Comparison of IS-NMF, KL-NMF and DR-NMF \n for rank-4 NMF of the audio dataset \n `Mary had a little lamb'''));
saveas(gcf, '../results/fig_Mary.png')
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。文章来源:https://www.toymoban.com/news/detail-468719.html

🌈4 Matlab代码、数据、文章讲解
到了这里,关于【分布鲁棒和多目标非负矩阵分解】基于DR-NMF的对NMF问题噪声模型的识别鲁棒性研究(Matlab代码实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!