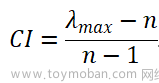前言
对于评价类模型,最好还是使用 Topsis法,主成分分析主观因素太大,灰色关联分析因为这个灰色理论近几年才在国内出现,使用范围较小,可能评委老师了解不多。模糊综合评价的话也可以使用,但是能用 Topsis法最好还用 Topsis法。
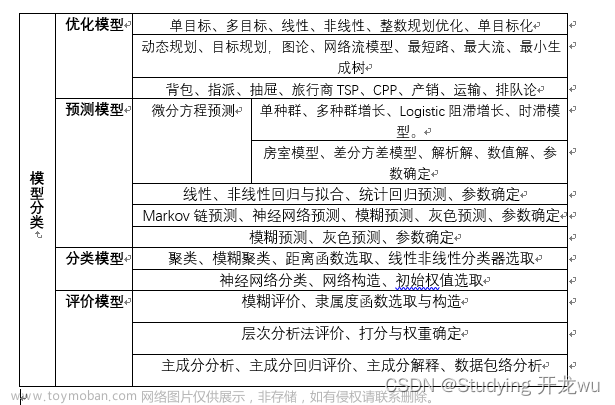
评价类模型主要研究的是多个指标中各个指标的评分来对不同指标进行评价。
一、层次分析法(AHP)
1.介绍
层次分析法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将定量分析与定性分析结合起来,用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以用定量方法解决的课题。
层次分析法的基本思路是将所要分析的问题层次化;根据问题的性质和所要达成的总目标,将问题分解为不同的组成因素,并按照这些因素的关联影响及其隶属关系,将因素按不同层次凝聚组合,形成一个多层次分析结构模型;最后,对问题进行优劣比较并排列。
2.算法流程

- 分析系统中各因素之间的关系,建立系统的递阶层次结构

- 对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)

- 由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验(检验通过权重才能用).


- 根据权重矩阵计算得分,并进行排序

3.局限性

二、优劣解距离法(Topsis法)
1.介绍
TOPSIS 法是一种常用的综合评价方法,其能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。基本过程为先将原始数据矩阵统一指标类型(一般正向化处理)得到正向化的矩阵,再对正向化的矩阵进行标准化处理以消除各指标量纲的影响,并找到有限方案中的最优方案和最劣方案,然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制,数据计算简单易行。
2.算法流程

- 将原始矩阵正向化

- 正向化矩阵标准化
注:标准化的目的是消除不同指标量纲的影响。 - 计算得分并归一化
3.模型拓展 —— 带权重的Topsis
1.使用层次分析法来确定权重取值

2.基于熵权法对Topsis模型的修正

熵权法的计算步骤
- 判断输入的矩阵中是否存在负数,如果有则要重新标准化到非负区间
(后面计算概率时需要保证每一个元素为非负数)
- 计算第 j 项指标下第 i 个样本所占的比重,并将其看作相对熵计算中用到的概率

- 计算每个指标的信息熵,并计算信息效用值,并归一化得到每个指标的熵权

三、灰色关联分析
1.介绍

2.算法流程
- 画统计图
- 确定分析数列

- 对变量进行预处理(两个目的:去量纲;缩小变量范围简化计算)
对母序列和子序列中的每个指标进行预处理:先求出每个指标的均值,再用改指标中的每个元素都除以其均值。 - 计算子序列中每个指标与母序列的关联系数

- 通过比较三个⼦序列和⺟序列的关联度可以得到结论
spassau中的算法步骤:
第一步:确定母序列和特征序列,且准备好数据格式;
第二步:针对数据进行无量纲化处理(通常情况下需要);
第三步:求解母序列和特征序列之间的灰色关联系数值;
第四步:求解关联度值;
第五步:对关联度值进行排序,得出结论。
3.注意事项

四、模糊综合评价模型
阅读:模糊综合评价模型详解
1.算法流程
第一步:确定评价指标和评语集;
第二步:确定权重向量矩阵A和构造权重判断矩阵R;
第三步:计算权重并进行决策评价。
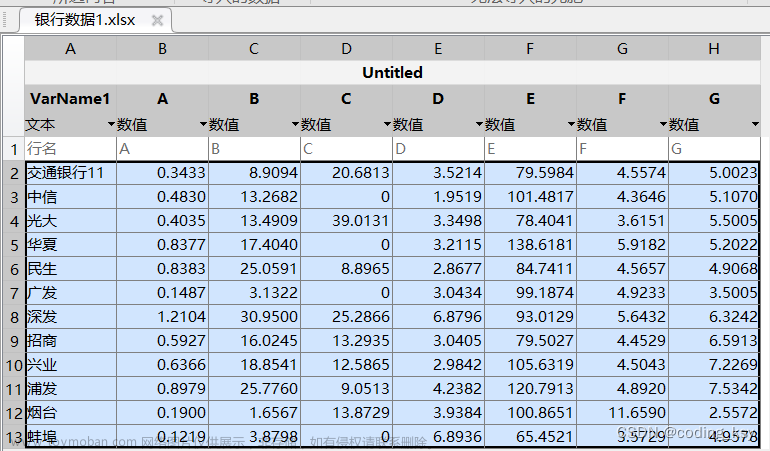
2.应用实例
 文章来源:https://www.toymoban.com/news/detail-468758.html
文章来源:https://www.toymoban.com/news/detail-468758.html
总结
补充阅读:
指标赋权与评价类方法总结
数模算法:模糊综合评价模型文章来源地址https://www.toymoban.com/news/detail-468758.html
到了这里,关于数学建模 —— 评价模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!