1. Toy模板网首页
  2. > Toy博客

算法27：最长回文子序列长度——范围模型

9月前 作者：chen_yao_kerr 分类：Toy博客 阅读(30) 违法举报

这篇具有很好参考价值的文章主要介绍了算法27：最长回文子序列长度——范围模型。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录

题目：

样本模型：

递归版本的范围模型

分析过程

动态规划版本

优化动态规划：

题目：

给定一个字符串str，返回这个字符串的最长回文子序列长度

比如 str = “a12b3c43def2ghi1kpm” * 最长回文子序列是“1234321”或者“123c321”，返回长度7

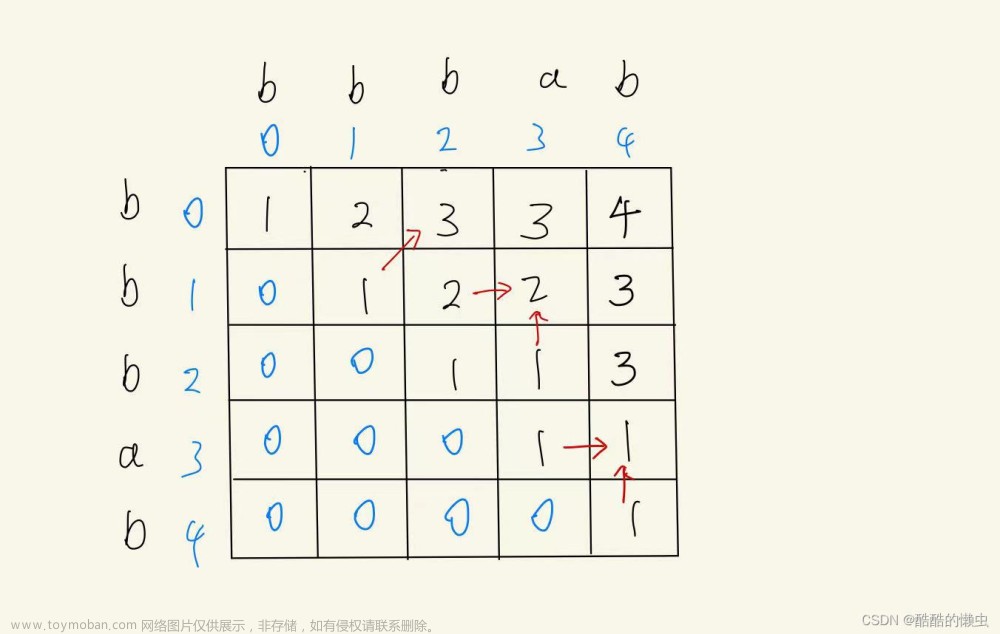
这一题使用样本模型，也可以解决，只需要生成一个逆序字符串就可以了。因为回文子序列，逆序以后，回文子序列依旧保持原来的顺序结构。

样本模型：

递归版本：

public static int longestPalindromeSubseq(String s)
    {
        if (s == null || s.isEmpty()) {
            return 0;
        }
        char[] s1 = s.toCharArray();
        char[] s2 = new char[s1.length];
        int position = 0;
        //生成逆序
        for (int i = s1.length-1; i >=0; i--) {
            s2[position++] = s1[i];
        }

        return process(s1, s2, s1.length-1, s2.length-1);
    }

    public static int process(char[] s1, char[] s2, int i, int j)
    {
        if (i == 0 && j == 0){
            return s1[i] == s2[j] ? 1 : 0;
        }
        else if (i == 0) {
            return  s1[i] == s2[j] ? 1 : process(s1, s2, i, j-1);
        }
        else if (j == 0) {
            return  s1[i] == s2[j] ? 1 : process(s1, s2, i-1, j);
        }
        else {

            int p1 = process(s1, s2, i, j-1);

            int p2 = process(s1, s2, i-1, j);

            int p3 = s1[i] == s2[j] ? process(s1, s2, i-1, j-1) + 1 : 0;

            return Math.max(p1, Math.max(p2, p3));
        }
    }

测试结果：

算法27：最长回文子序列长度——范围模型

动态规划版本： 

package code03.动态规划_07;

/**
 * 给定一个字符串str，返回这个字符串的最长回文子序列长度
 * 比如 ： str = “a12b3c43def2ghi1kpm”
 * 最长回文子序列是“1234321”或者“123c321”，返回长度7
 *
 * https://leetcode.com/problems/longest-palindromic-subsequence/
 */
public class PalindromeSubsequence_05
{
    public static int longestPalindromeSubseq(String str) {

        if (str == null || str.isEmpty()) {
            return 0;
        }
        char[] s1 = str.toCharArray();
        char[] s2 = new char[s1.length];
        int position = 0;
        //生成逆序
        for (int i = s1.length-1; i >=0; i--) {
            s2[position++] = s1[i];
        }

        //以s1做行，s2做列
        int[][] dp = new int[ s1.length][s2.length];

        int index1 = s1.length - 1;
        int index2 = s2.length - 1;

        //根据递归   if (index1 == 0 && index2 == 0)  而来
        dp[0][0] = s1[0] == s2[0] ? 1 : 0;

        //根据递归  else if (index1 == 0)  而来, 此处代表先处理 第一行的所有列
        for (int i = 1; i <= index2; i++) {
            dp[0][i] = s1[0] == s2[i] ? 1 : dp[0][i-1];
        }

        //根据递归  else if (index2 == 0)  而来, 此处代表先处理 第一列的所有行
        for (int j = 1; j <= index1; j++) {
            dp[j][0] = s1[j] == s2[0] ? 1 : dp[j-1][0];
        }

        //通用case  根据递归中最后一个else而来
        for (int row = 1; row <= index1; row++) {
            for (int col = 1; col <= index2; col++) {

                //根据 int p1 =  process(s1, s2, index1, index2-1) 改写
                int p1 = dp[row][col - 1];

                //根据 int p2 =  process(s1, s2, index1-1, index2) 改写
                int p2 = dp[row -1][col];

                //int p3 = s1[index1] == s2[index2] ? (process(s1, s2, index1-1, index2-1) + 1) : 0;
                int p3 = s1[row] == s2[col] ? (dp[row -1][col -1] + 1) : 0;

                dp[row][col] = Math.max(p1, Math.max(p2, p3));
            }
        }

        //返回值对应递归中的下标
        return dp[index1][index2];
    }
}

算法27：最长回文子序列长度——范围模型

样本模型，在上一篇已经详细的说过了，具体推导过程可以参照 算法27：最长公共子序列——样本模型（4）_chen_yao_kerr的博客-CSDN博客

样本模型，都是以样本的最后一个元素为基础进行讨论分析的。

而范围模型，则是以样本数据的  开头  和  结尾   进行讨论的。

递归版本的范围模型

package code03.动态规划_07;

/**
 * 给定一个字符串str，返回这个字符串的最长回文子序列长度
 * 比如 ： str = “a12b3c43def2ghi1kpm”
 * 最长回文子序列是“1234321”或者“123c321”，返回长度7
 *
 * https://leetcode.com/problems/longest-palindromic-subsequence/
 */
public class PalindromeSubsequence_05_opt1
{
    public static int longestPalindromeSubseq(String str)
    {
        if (str == null || str.isEmpty()) {
            return 0;
        }

        return process(str.toCharArray(), 0, str.length() -1);
    }

    //范围模型，需要讨论样本数据的开头和结尾
    public static int process(char[] str, int left, int right)
    {
        //如果长度为1,也就是说字符串只有一个字符
        if (left == right) {
            return 1;
        }

        //字符串只有2个元素. 如果第一个元素和第二个元素相同，则说明回文
        //长度为2. 否则，最长子回文只有1，因为我们默认的子序列回文长度就是为1.
        if (left == right -1) {
            return str[left] == str[right] ? 2 : 1;
        }

        /**
         * 最长回文子序列, 有可能出现以下情况
         * 1. 包含结尾，不包含开头
         * 2. 包含开头，不包含结尾
         * 3. 既不包含开头，也不包含结尾
         * 4. 既包含开头，也包含结尾
         */

        //包含结尾，不包含开头
        int p1 = process(str, left + 1, right);
        //包含开头，不包含结尾
        int p2 = process(str, left, right - 1);
        //既不包含开头，也不包含结尾
        int p3 = process(str, left + 1, right - 1);
        //既包含开头，也包含结尾
        int p4 = str[left] != str[right] ? 0 : (2 + process(str, left + 1, right - 1));
        //也可以改写成 int p4 = str[left] != str[right] ? 0 : (2 + p3);
        
        return Math.max(Math.max(p1, p2), Math.max(p3, p4));
    }


    public static void main(String[] args) {
        System.out.println(longestPalindromeSubseq("a12b3c43def2ghi1kpm"));
    }
}

测试结果： 

算法27：最长回文子序列长度——范围模型

分析过程

1. 假设字符串为 a12a21b，我们知道最长回文子序列为12a21, 那么它的长度就是5.

2. 构建二维数组.  行和列都是数组的下标。递归的传入参数 0 和  str.length() -1，分别代表数组的左边开始位置和右边开始位置。将left作为行，right作为列，那么可以推导出如下的表格信息

0(a) 1(1) 2(2) 3(a) 4(2) 5(1) 6(b)
0(a)
1(1) x
2(2) x x
3(a) x x x
4(2) x x x x
5(1) x x x x x
6(b) x x x x x x

3. 根据递归的

if (left == right) {
    return 1;
}

可以推算出对角线全部为 1.

0(a) 1(1) 2(2) 3(a) 4(2) 5(1) 6(b)
0(a) 1
1(1) x 1
2(2) x x 1
3(a) x x x 1
4(2) x x x x 1
5(1) x x x x x 1
6(b) x x x x x x 1

4. 根据递归

if (left == right -1) {
    return str[left] == str[right] ? 2 : 1;
}

可以推算出：

0(a) 1(1) 2(2) 3(a) 4(2) 5(1) 6(b)
0(a) 1 1
1(1) x 1 1
2(2) x x 1 1
3(a) x x x 1 1
4(2) x x x x 1 1
5(1) x x x x x 1 1
6(b) x x x x x x 1

5.  核心推算过程

//包含结尾，不包含开头。我们知道（left，right）依赖（left+1, right）,即下一行
int p1 = process(str, left + 1, right);
//包含开头，不包含结尾. 我们知道（left，right）依赖（left, right -1）即前一列
int p2 = process(str, left, right - 1);
//既不包含开头，也不包含结尾。我们知道（left，right）依赖（left+1, right -1）即前一列的下一行
int p3 = process(str, left + 1, right - 1);
//既包含开头，也包含结尾。我们知道（left，right）依赖（left+1, right -1）即前一列的下一行
int p4 = str[left] != str[right] ? 0 : (2 + process(str, left + 1, right - 1));

也就是说（left，right）依赖当前行的前一列、下一行的当前列 和 前一行的前一列/

也就是说想要知道dp[4][6]的值，必须先知道dp[4][5]  dp[5][6] 和 dp[5][5] 的值。而这几个值已经推出来了，那就拿到最大值 1.

0(a) 1(1) 2(2) 3(a) 4(2) 5(1) 6(b)
0(a) 1 1
1(1) x 1 1
2(2) x x 1 1
3(a) x x x 1 1
4(2) x x x x 1 1
5(1) x x x x x 1 1
6(b) x x x x x x 1

 还是按照以上的信息，根据前一列、下一行的当前列 以及前一行的前一列可以推算出结果。

以dp[3][6]为例子。 dp[3][5]为3， dp[4][6]为3，dp[4][5]为1. 并且字符串下标3的值为a，6的位置为b， a!=b, 因此维持最大值3. 如果相等，那就额外再加 2。

                                                依次类推，第一个变化的位置为dp[2][4]

0(a) 1(1) 2(2) 3(a) 4(2) 5(1) 6(b)
0(a) 1 1 1
1(1) x 1 1 1
2(2) x x 1 1 3
3(a) x x x 1 1 1
4(2) x x x x 1 1 1
5(1) x x x x x 1 1
6(b) x x x x x x 1

                                        依次类推，得到完整的表格信息

0(a) 1(1) 2(2) 3(a) 4(2) 5(1) 6(b)
0(a) 1 1 1 3 3 5 5
1(1) x 1 1 1 3 5 5
2(2) x x 1 1 3 3 3
3(a) x x x 1 1 1 1
4(2) x x x x 1 1 1
5(1) x x x x x 1 1
6(b) x x x x x x 1

动态规划版本

package code03.动态规划_07;

/**
 * 给定一个字符串str，返回这个字符串的最长回文子序列长度
 * 比如 ： str = “a12b3c43def2ghi1kpm”
 * 最长回文子序列是“1234321”或者“123c321”，返回长度7
 *
 * https://leetcode.com/problems/longest-palindromic-subsequence/
 */
public class PalindromeSubsequence_05_opt2
{
    public static int longestPalindromeSubseq(String str)
    {
        if (str == null || str.isEmpty()) {
            return 0;
        }

        //构造一个 n * n的矩阵
        char[] s = str.toCharArray();
        int[][] dp = new int[s.length][s.length];

        //最后一行的最后一列比较特殊，会出现数组越界，需要单独设置
        dp[s.length-1][s.length-1] = 1;
        for (int i = 0; i < s.length - 1 ; i++) {
            //根据递归  if (left == right) 得到对角线全部为1
            dp[i][i] = 1;
            //根据递归 if (left == right -1) { 得到对角线的后一列值
            dp[i][i+1] = s[i] == s[i+1] ? 2 : 1;
        }

        //由于倒数第一、第二行已经推算出来了，因此从倒数第三行开始推算
        for (int row = s.length - 3; row >= 0; row--)
        {
            //从倒数第一行开始推算。并且列需要随着行变化而变化
            for (int col = row + 2; col < s.length ; col++)
            {
                //包含开头，不包含结尾
                int p1 = dp[row + 1][col];
                //包含结尾，不包含开头
                int p2 = dp[row][col - 1];
                //既不包含开头，也不包含结尾
                int p3 =  dp[row + 1][col - 1];
                //既包含开头，也包含结尾
                int p4 = s[row] != s[col] ? 0 : (2 + dp[row + 1][col - 1]);

                dp[row][col] = Math.max(Math.max(p1, p2), Math.max(p3, p4));
            }
        }

        return dp[0][s.length-1];
    }



    public static void main(String[] args) {
        System.out.println(longestPalindromeSubseq("a12b3c43def2ghi1kpm"));
    }
}

测试结果：

算法27：最长回文子序列长度——范围模型

优化动态规划：

0(a) 1(1) 2(2) 3(a) 4(2) 5(1) 6(b)
0(a) 1 1 1
1(1) x 1 1 1
2(2) x x 1 1 3
3(a) x x x 1 1 1
4(2) x x x x 1 1 1
5(1) x x x x x 1 1
6(b) x x x x x x 1

dp[2][4]位置是第一次发生变化的。下一轮，我们会推算出如下结果：

0(a) 1(1) 2(2) 3(a) 4(2) 5(1) 6(b)
0(a) 1 1 1 3
1(1) x 1 1 1 3
2(2) x x 1 1 3 3
3(a) x x x 1 1 1 1
4(2) x x x x 1 1 1
5(1) x x x x x 1 1
6(b) x x x x x x 1

而dp[1][5]位置依赖 dp[1][4] 、 dp[2][5] 和 dp[2][4]. 

但是dp[1][4] 和  [2][5]已经推算出来了，他们都依赖dp[2][4]。

也就是说dp[1][4] 和  [2][5]至少都是大于或等于dp[2][4位置的数据的，

我们的逻辑是获取到最大值，既然能够拿到大于等于它的值，那么dp[1][5]直接依赖dp[1][4] 和  [2][5]就可以了，没必要再去依赖较小的dp[2][4]值了。

因此，单独的依赖左下方，即p3就可以省略

递归优化：

package code03.动态规划_07;

/**
 * 给定一个字符串str，返回这个字符串的最长回文子序列长度
 * 比如 ： str = “a12b3c43def2ghi1kpm”
 * 最长回文子序列是“1234321”或者“123c321”，返回长度7
 *
 * https://leetcode.com/problems/longest-palindromic-subsequence/
 */
public class PalindromeSubsequence_05_opt1
{
    public static int longestPalindromeSubseq(String str)
    {
        if (str == null || str.isEmpty()) {
            return 0;
        }

        return process(str.toCharArray(), 0, str.length() -1);
    }

    //范围模型，需要讨论样本数据的开头和结尾
    public static int process(char[] str, int left, int right)
    {
        //如果长度为1,也就是说字符串只有一个字符
        if (left == right) {
            return 1;
        }

        //字符串只有2个元素. 如果第一个元素和第二个元素相同，则说明回文
        //长度为2. 否则，最长子回文只有1，因为我们默认的子序列回文长度就是为1.
        if (left == right -1) {
            return str[left] == str[right] ? 2 : 1;
        }

        /**
         * 最长回文子序列, 有可能出现以下情况
         * 1. 包含结尾，不包含开头
         * 2. 包含开头，不包含结尾
         * 3. 既不包含开头，也不包含结尾
         * 4. 既包含开头，也包含结尾
         */

        //包含结尾，不包含开头
        int p1 = process(str, left + 1, right);
        //包含开头，不包含结尾
        int p2 = process(str, left, right - 1);
        //既不包含开头，也不包含结尾
        //int p3 = process(str, left + 1, right - 1);
        //既包含开头，也包含结尾
        int p4 = str[left] != str[right] ? 0 : (2 + process(str, left + 1, right - 1));

        return Math.max(Math.max(p1, p2), p4);
    }


    public static void main(String[] args) {
        System.out.println(longestPalindromeSubseq("a12b3c43def2ghi1kpm"));
    }
}

动态规划版本优化：文章来源地址https://www.toymoban.com/news/detail-468872.html

package code03.动态规划_07;

/**
 * 给定一个字符串str，返回这个字符串的最长回文子序列长度
 * 比如 ： str = “a12b3c43def2ghi1kpm”
 * 最长回文子序列是“1234321”或者“123c321”，返回长度7
 *
 * https://leetcode.com/problems/longest-palindromic-subsequence/
 */
public class PalindromeSubsequence_05_opt2
{
    public static int longestPalindromeSubseq(String str)
    {
        if (str == null || str.isEmpty()) {
            return 0;
        }

        //构造一个 n * n的矩阵
        char[] s = str.toCharArray();
        int[][] dp = new int[s.length][s.length];

        //最后一行的最后一列比较特殊，会出现数组越界，需要单独设置
        dp[s.length-1][s.length-1] = 1;
        for (int i = 0; i < s.length - 1 ; i++) {
            //根据递归  if (left == right) 得到对角线全部为1
            dp[i][i] = 1;
            //根据递归 if (left == right -1) { 得到对角线的后一列值
            dp[i][i+1] = s[i] == s[i+1] ? 2 : 1;
        }

        //由于倒数第一、第二行已经推算出来了，因此从倒数第三行开始推算
        for (int row = s.length - 3; row >= 0; row--)
        {
            //从倒数第一行开始推算。并且列需要随着行变化而变化
            for (int col = row + 2; col < s.length ; col++)
            {
            /*    //包含开头，不包含结尾
                int p1 = dp[row + 1][col];
                //包含结尾，不包含开头
                int p2 = dp[row][col - 1];
                //既不包含开头，也不包含结尾
                int p3 =  dp[row + 1][col - 1];
                //既包含开头，也包含结尾
                int p4 = s[row] != s[col] ? 0 : (2 + dp[row + 1][col - 1]);

                dp[row][col] = Math.max(Math.max(p1, p2), Math.max(p3, p4));*/

                //包含开头，不包含结尾
                int p1 = dp[row + 1][col];
                //包含结尾，不包含开头
                int p2 = dp[row][col - 1];
                dp[row][col] = Math.max(p1, p2);

                if (s[row] == s[col] ) {
                    dp[row][col] = Math.max(dp[row][col], 2 + dp[row + 1][col - 1]);
                }
            }
        }
        return dp[0][s.length-1];
    }



    public static void main(String[] args) {
        System.out.println(longestPalindromeSubseq("a12b3c43def2ghi1kpm"));
    }
}

到了这里，关于算法27：最长回文子序列长度——范围模型的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • LeetCode刷题 | 647. 回文子串、516. 最长回文子序列

    LeetCode刷题 | 647. 回文子串、516. 最长回文子序列

    给你一个字符串  s  ，请你统计并返回这个字符串中  回文子串  的数目。 回文字符串  是正着读和倒过来读一样的字符串。 子字符串  是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

    2024年02月12日
    浏览(44)

  • Day 57|647. 回文子串| 516.最长回文子序列

    ● 647. 回文子串 ● 516.最长回文子序列 ● 动态规划总结篇 难

    2024年02月16日
    浏览(45)
  • leetcode 516. 最长回文子序列(JAVA)题解

    leetcode 516. 最长回文子序列(JAVA)题解

    题目链接 https://leetcode.cn/problems/longest-palindromic-subsequence/description/?utm_source=LCUSutm_medium=ip_redirectutm_campaign=transfer2china 目录 题目描述： 暴力递归： 动态规划： 给你一个字符串  s  ，找出其中最长的回文子序列，并返回该序列的长度。子序列定义为：不改变剩余字符顺序的情况

    2024年02月13日
    浏览(41)
  • ( 动态规划) 516. 最长回文子序列 ——【Leetcode每日一题】

    ( 动态规划) 516. 最长回文子序列 ——【Leetcode每日一题】

    难度：中等 给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。 子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。 示例 1： 输入：s = “bbbab” 输出：4 解释：一个可能的最长回文子序列为 “bbbb” 。 示例

    2024年02月06日
    浏览(42)
  • 每天一道leetcode：516. 最长回文子序列（动态规划&中等）

    每天一道leetcode：516. 最长回文子序列（动态规划&中等）

    给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。 子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。 1 = s.length = 1000 s 仅由小写英文字母组成 动态规划 ，使用二维dp数组记录[i,j]间的最大回文子序列长度

    2024年02月13日
    浏览(45)
  • 动态规划学习——最长回文子序列，让字符串变成回文串的最小插入次数

    动态规划学习——最长回文子序列，让字符串变成回文串的最小插入次数

    1.题目 给你一个字符串  s  ，找出其中最长的回文子序列，并返回该序列的长度。 子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。 示例 1： 示例 2： 提示： 1 = s.length = 1000 s  仅由小写英文字母组成 2.题目接口  3.解题思路

    2024年02月04日
    浏览(54)
  • C++---最长上升子序列模型---最大上升子序列和（每日一道算法2023.3.3）

    C++---最长上升子序列模型---最大上升子序列和（每日一道算法2023.3.3）

    注意事项： 本题为\\\"线性dp—最长上升子序列的长度\\\"的扩展题，所以dp思路这里就不再赘述。 题目： 比如，对于序列(1,7,3,5,9,4,8)，有它的一些上升子序列，如(1,7),(3,4,8)等。 这些子序列中和最大为18，为子序列(1,3,5,9)的和。 你的任务，就是对于给定的序列，求出最大上升子序

    2024年02月03日
    浏览(37)

  • 代码随想录 Day - 59｜#647 回文字串｜#516 最长回文子序列

    ● 647. 回文字串 ● 516. 最长回文子序列 给你一个字符串 s ，请你统计并返回这个字符串中回文子串的数目。 回文字符串是正着读和倒过来读一样的字符串。 子字符串是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串，即使是由相同的字符组成

    2024年02月07日
    浏览(39)

  • 最长回文子序列问题的原理与实现：动态规划的又一经典应用

    回文是指一个正着读和反着读都一样的字符串，比如 “aba” ， “racecar” ， “madam” 等。回文有许多有趣的性质和应用，比如在密码学，生物信息学，数据压缩等领域都有涉及。 那么，给定一个字符串，如何找出它的最长回文子序列呢？最长回文子序列是指从原字符串中删

    2023年04月13日
    浏览(49)

  • 【python】求最长连续公共子序列长度的几种解法

      给定两个序列X和Y,返回最长连续的公共子序列长度。如果没有连续公共子序列，返回0. X和Y的元素都是整数。 示例： 输入： 1 5 7 3 4 5 7 3 4 4 5 7 -2 输出： 3  说明： 最长的连续公共子序列是[7,3,4] (X[2:4] 和Y[0:2]) 这道题在【leetcode1143】的基础上增加了公共子序列连续的限制。

    2024年02月10日
    浏览(45)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包