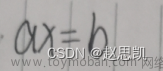一、简化矩阵
（1）阶梯形矩阵
1.1.1 定义
a. 如果矩阵有零行（ 元素全为 0 的行 ）， 零行 全在下面；
b. 各非零行的第一个非零元素列标随行标增大而增大；
1.1.2 展示
下图两个矩阵都是阶梯矩阵
（2）最简化矩阵
1.1.1 定义
a. 各非零行的首非零元素（主元）都是 1；
b. 所有的首非零元所在的列的其余元素都为 0 ；
c. 最简化矩阵是一个阶梯矩阵；
1.1.2 展示
下图两个矩阵都是最简化矩阵
二、主元和自由变量
（1）定义
2.1.1 主元
行阶梯矩阵中每一行左起第一个非零元素所代表的未知数就叫做主元；
2.1.1 自由变量
矩阵中除主元外的元素变量叫自由变量；
（2）自由变量的取值规则
只有一个自由变量赋值为 1 ；
两个自由变量赋值为 ( 0 1 )^T 和 ( 1 0 )^T ；
三个自由变量赋值为( 0 0 1 )^T 、 ( 0 1 0 )^T 、( 1 0 0 )^T ；
…… ……
（ 自由变量并非只能按上述规则取值，但是取 0、1 对于最简化阶梯型计算比较简单，且能保证特征之间线性无关 ）
三、通解、 特解、基础解系的计算
例：
（1）
解：
（2）
解：文章来源：https://www.toymoban.com/news/detail-468916.html
文章来源地址https://www.toymoban.com/news/detail-468916.html
到了这里，关于线性代数（7）：矩阵的应用的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
