【动手学深度学习】现代卷积神经网络汇总-Toy模板网

这篇具有很好参考价值的文章主要介绍了【动手学深度学习】现代卷积神经网络汇总。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文为作者阅读学习李沐老师《动手学深度学习》一书的阶段性读书总结，原书地址为：Dive into Deep Learning。

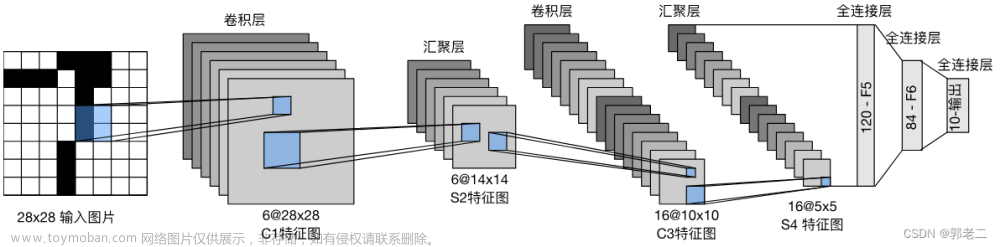
1 LeNet

网络结构

实现代码

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

网络特征
1. 最早发布的卷积神经网络之一。
2. 每个卷积块中的基本单元是一个卷积层、一个sigmoid激活函数和平均汇聚层。

2 AlexNet

网络结构

实现代码

net = nn.Sequential(
    # 这里使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

网络特征
1. AlexNet通过暂退法（dropout）控制全连接层的模型复杂度，而LeNet只使用了权重衰减。
2. AlexNet在训练时增加了大量的图像增强数据，如翻转、裁切和变色。这使得模型更健壮，更大的样本量有效地减少了过拟合。
3. AlexNet将sigmoid激活函数改为更简单的ReLU激活函数。
4. AlexNet比相对较小的LeNet5要深得多。AlexNet由八层组成：五个卷积层、两个全连接隐藏层和一个全连接输出层。

3 VGG

网络结构
实现代码

import torch
from torch import nn
from d2l import torch as d2l


def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    # 卷积层部分
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(
        *conv_blks, nn.Flatten(),
        # 全连接层部分
        nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10))
   
conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))
net = vgg(conv_arch)

网络特征
1. 块的使用导致网络定义的非常简洁。使用块可以有效地设计复杂的网络。
2. 在VGG论文中，Simonyan和Ziserman尝试了各种架构。特别是他们发现深层且窄的卷积（即3×3）比较浅层且宽的卷积更有效。

4 NiN

网络结构

【动手学深度学习】现代卷积神经网络汇总

实现代码

import torch
from torch import nn
from d2l import torch as d2l


def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

网络特征
1. NiN完全取消了全连接层。因为如果和LeNet、AlexNet和VGG一样使用了全连接层，可能会完全放弃表征的空间结构。
2. 使用1x1卷积层，作为在每个像素通道维度上独立作用的全连接层。

5 GoogLeNet

网络结构
1. Inception块结构
2. GoogLeNet网络结构

实现代码

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)
    
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1,1)),
                   nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

网络特征
1. 网络结构中含有并行联结。并行联结各个路径的权重通过最终的通道数占比来体现。

6 ResNet

网络结构
1. 包含以及不包含 1×1 卷积层的残差块
2. ResNet网络结构

实现代码

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Residual(nn.Module):
    def __init__(self, in_channels, num_channels, use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1=nn.Conv2d(in_channels, num_channels, stride=strides, padding=1, kernel_size=3)
        self.conv2=nn.Conv2d(num_channels, num_channels, kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3=nn.Conv2d(in_channels, num_channels, kernel_size=1, stride=strides)
        else:
            self.conv3=None
        self.bn1=nn.BatchNorm2d(num_channels)
        self.bn2=nn.BatchNorm2d(num_channels)
        
    def forward(self, x):
        y=F.relu(self.bn1(self.conv1(x)))
        y=self.bn2(self.conv2(y))
        if self.conv3:
            x=self.conv3(x)
        y+=x
        return F.relu(y)
    
b1=nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                nn.BatchNorm2d(64), nn.ReLU(),
                nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2=nn.Sequential(Residual(64, 64), Residual(64, 64))
b3=nn.Sequential(Residual(64, 128, use_1x1conv=True, strides=2), 
                Residual(128, 128))
b4=nn.Sequential(Residual(128, 256, use_1x1conv=True, strides=2), 
                Residual(256, 256))
b5=nn.Sequential(Residual(256, 512, use_1x1conv=True, strides=2), 
                Residual(512, 512))
net=nn.Sequential(b1, b2, b3, b4, b5,
                 nn.AdaptiveAvgPool2d((1, 1)),
                 nn.Flatten(), nn.Linear(512, 10))

网络特征
1. 残差网络可以认为是加入了快速通道得到f(x)=g(x)+x。
2. 残差块使得很深的网络更加容易训练。
3. 应用了批量规范化层，利用小批量的均值和标准差，不断调整神经网络的中间输出，使整个神经网络各层的中间输出值更加稳定。加速网络训练，并不会提高准确率。

7 DenseNet

网络结构

实现代码

import torch
from torch import nn
from d2l import torch as d2l


def conv_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))
    
class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(
                num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输入和输出
            X = torch.cat((X, Y), dim=1)
        return X
    
def transition_block(input_channels, num_channels):
    # 由于每个稠密块都会带来通道数的增加，使用过多则会过于复杂化模型。 而过渡层可以用来控制模型复杂度。
    # 它通过卷积层来减小通道数，并使用步幅为2的平均汇聚层减半高和宽，从而进一步降低模型复杂度。
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))
    
b1 = nn.Sequential(
    nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
    nn.BatchNorm2d(64), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
# num_channels为当前的通道数
num_channels, growth_rate = 64, 32
num_convs_in_dense_blocks = [4, 4, 4, 4]
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
    blks.append(DenseBlock(num_convs, num_channels, growth_rate))
    # 上一个稠密块的输出通道数
    num_channels += num_convs * growth_rate
    # 在稠密块之间添加一个转换层，使通道数量减半
    if i != len(num_convs_in_dense_blocks) - 1:
        blks.append(transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2
net = nn.Sequential(
    b1, *blks,
    nn.BatchNorm2d(num_channels), nn.ReLU(),
    nn.AdaptiveAvgPool2d((1, 1)),
    nn.Flatten(),
    nn.Linear(num_channels, 10))

网络特征文章来源地址https://www.toymoban.com/news/detail-468922.html
1. 在跨层连接上，不同于ResNet中将输入与输出相加，稠密连接网络（DenseNet）在通道维上连结输入与输出。
2. DenseNet的主要构建模块是稠密块和过渡层。前者定义如何连接输入和输出，而后者则通过1x1卷积层控制通道数量，使其不会太复杂。