人工智能及其应用(蔡自兴)期末复习
本文是基于郑州大学人工智能课程制作的复习笔记,教学内容基本很陈旧,应该很久都不会更新。
⭐️ 都是我们的复习重点,需要进行关注
人工智能太恶心了,内容太多了!
注:我只是按照我们的课件来进行复习,不要盲目相信我的主观观点!!! 每年教的老师是不一样的,课件也是不一样的!!! 我们当年的老师是 tz、wzc
😋 更多复习科目请查看: 2020级郑州大学物联网工程期末记录 😋
原Markdown文件获取请跳转:https://github.com/anda522/CourseReview
相关资料:
人工智能期末复习
人工智能复习题
人工智能模拟卷
人工智能期末练习题
1 ⭐️绪论
人工智能:人工智能就是用人工的方法在机器(计算机)上实现的智能,或称机器智能、计算机智能。
人工智能发展的三个阶段:
- 计算
- 感知
- 认知
⭐️人工智能发展时期:
-
孕育期 ( 1956年前):亚里士多德,莱布尼茨,图灵,莫克,麦克洛奇和皮兹,维纳
-
形成期 ( 1956-1970年):1956年第一次人工智能研讨会(达特茅斯会议),
-
暗淡期 ( 1966-1974年):过高预言
-
知识应用期 ( 1970-1988年):专家系统的出现
-
集成发展期 ( 1986年至今):AI技术进一步研究
⭐️人工智能学派:
- 符号主义(功能模拟方法):逻辑主义,以物理符号系统为原理,代表:纽厄尔,肖,西蒙,尼尔逊
- 连接主义(结构模拟方法):仿生学派,神经网络之间连接机制为原理,代表:卡洛克,皮茨,霍普菲尔德,鲁梅尔哈特
- 行为主义(行为模拟方法):控制论学派,类似于控制机器人,代表:布鲁克斯
人工智能应用:问题求解和博弈,逻辑推理和定理证明,计算智能,分布式人工智能和真体,自动程序设计,专家系统,机器学习,自然语言理解,机器人学,模式识别,机器视觉,神经网络,智能控制
人工智能系统分类:专家系统,模糊系统,神经网络系统,学习系统,仿生系统,群智能系统,多真体系统,混合智能系统
目标:
- 近期目标:建造智能计算机代替人类的部分智力劳动
- 远期目标:揭示人类智能的根本机理,用智能机器去模拟、延伸和扩展人类的智能
研究的基本内容:认知建模,知识表示,知识推理,知识应用,机器感知,机器思维,机器学习,机器行为,智能系统构建
2 知识表示
2.1 ⭐️状态空间表示
概念理解:状态,算符
状态表示(知道初始状态和目标状态),状态表示图的画法
相关问题:
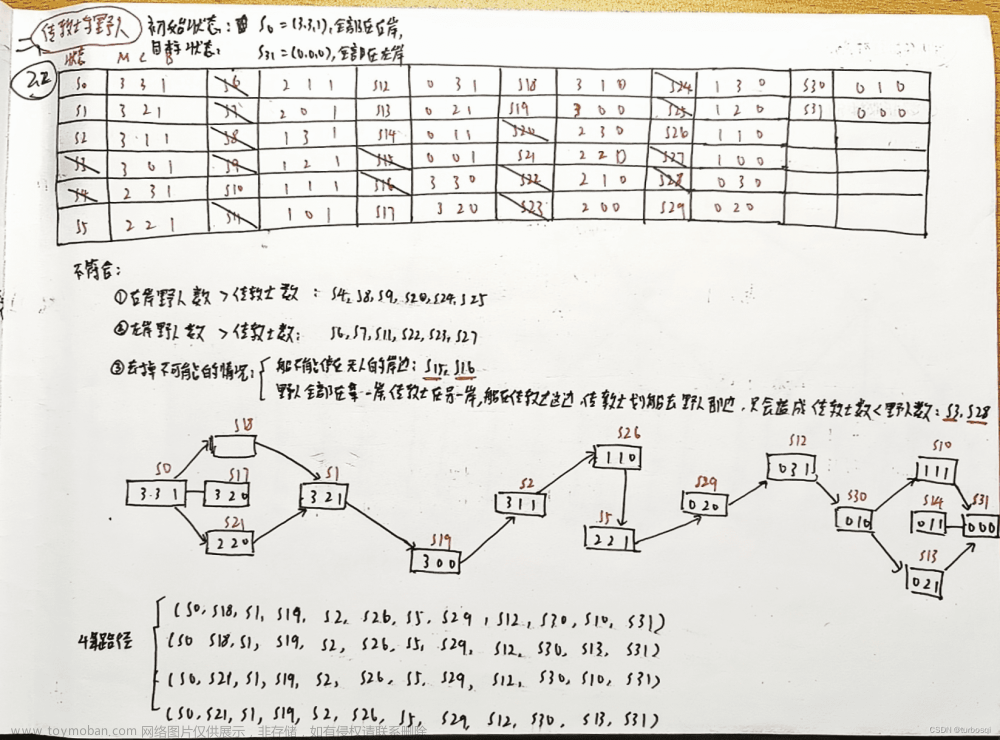
- 野人传教士渡河问题
( a , b , c ) (a, b, c) (a,b,c)表示(左岸传教士人数,左岸野人数,左岸船数)
- 梵塔问题
状态:
(
S
A
,
S
B
)
(S_A, S_B)
(SA,SB),
S
A
S_A
SA表示
A
A
A所在杆号,
S
B
S_B
SB表示
B
B
B所在杆号,
S
A
,
S
B
∈
{
1
,
2
,
3
}
S_A,S_B \in \{1, 2, 3\}
SA,SB∈{1,2,3},全部状态为:
(
1
,
1
)
,
(
1
,
2
)
,
(
1
,
3
)
,
(
2
,
1
)
,
(
2
,
2
)
,
(
2
,
3
)
,
(
3
,
1
)
,
(
3
,
2
)
,
(
3
,
3
)
(1,1), (1, 2), (1, 3), (2, 1), (2, 2),(2,3),(3,1),(3,2),(3,3)
(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)
初始状态:
(
1
,
1
)
(1,1)
(1,1),目标状态:
(
3
,
3
)
(3,3)
(3,3)
状态空间图:

- 八数码问题
2.2 ⭐️归约表示(与或图)
需要理解:归约表示思路,与或图表示
- 梵塔问题(四阶为例)
假设用向量 ( D 4 , D 3 , D 2 , D 1 ) (D_4, D_{3},D_2, D_1) (D4,D3,D2,D1)表示从大到小的圆盘所在的柱子号,则
初始状态: ( 1 , 1 , 1 , 1 ) (1, 1, 1, 1) (1,1,1,1)
目标状态: ( 3 , 3 , 3 , 3 ) (3, 3, 3, 3) (3,3,3,3)
问题归约为子问题:
- 移动3,2,1号圆盘至2号柱子
- 移动4号圆盘至3号柱子
- 移动3,2,1号圆盘至3号柱子
归约图表示:

2.3 谓词逻辑表示
概念理解:谓词,项,谓词公式,原子公式,合式公式
合式公式性质:


自然语言转换成谓词:
-
人都会死
( ∀ x ) ( m a n ( x ) → d i e ( x ) ) (\forall x) (man(x) \to die(x)) (∀x)(man(x)→die(x)) -
有的人聪明
( ∃ x ) ( m a n ( x ) → c l e v e r ( x ) ) (\exist x) (man(x) \to clever(x)) (∃x)(man(x)→clever(x))
谓词推理:
下面的例子使用了
P
∨
Q
¬
P
∨
Q
⟹
Q
∨
Q
=
Q
P \lor Q \hspace{1em} \neg P \lor Q \implies Q \lor Q = Q
P∨Q¬P∨Q⟹Q∨Q=Q 消解推理规则
2.4 语义网络表示
常用语义联系:


推理机制:匹配和继承
2.5 框架表示
结构:
- 节点
- 槽:每个槽可有多个侧面,每个侧面可有多个值
- 值
推理机制:
- 匹配
- 填槽(查询,默认,继承,附加过程计算)
大学教师的框架:

2.6 ⭐️知识表示方法的联系

3 搜索推理
3.1 ⭐️盲目搜索(无信息搜索)
本小节没有加以整理,请看课件
- ⭐️深度优先搜素
- ⭐️宽(广)度优先搜索
- 等代价搜索(UCS):就是
Dijkstra算法 - 有界深搜:就是限制深度的深搜
- 迭代加深算法(IDS)
知道OPEN表和CLOSED表的作用
3.2 ⭐️启发式搜索(有信息搜索)
按选择范围不同分为:全局择优搜索(A,A*)和局部择优搜素
f
(
x
)
=
g
(
x
)
+
h
(
x
)
f(x) = g(x) + h(x)
f(x)=g(x)+h(x)
h
(
x
)
h(x)
h(x):启发函数
搜索算法:
-
A算法: h ( x ) h(x) h(x)不做限制 -
A*算法: h ( x ) h(x) h(x)有限制
3.3 ⭐️消解原理(归结原理)
就是对几个子句推导出新的子句(几个公理推导出新的结论)
- ⭐️如何求子句集(将谓词演算公式化成子句集)P97
子句集特征:没有蕴涵词( → \rightarrow →)、等值词( ↔ , ≡ \leftrightarrow, \equiv ↔,≡), ¬ \neg ¬作用原子谓词,没有全称和存在量词,合取范式,元素之间变元不同,集合形式

- ⭐️消解推理规则
P ¬ P ∨ Q ⟹ Q P ∨ Q ¬ P ∨ Q ⟹ Q ∨ Q = Q ¬ P P ⟹ N I L ¬ P ∨ R ( P → R ) ¬ Q ∨ R ( Q → R ) ⟹ ¬ P ∨ Q ( P → Q ) P \hspace{1em} \neg P \lor Q \implies Q \\ P \lor Q \hspace{1em} \neg P \lor Q \implies Q \lor Q = Q \\ \neg P \hspace{1em} P \implies NIL \\ \neg P \lor R(P \to R) \hspace{1em} \neg Q \lor R(Q \to R) \implies \neg P \lor Q(P \to Q) P¬P∨Q⟹QP∨Q¬P∨Q⟹Q∨Q=Q¬PP⟹NIL¬P∨R(P→R)¬Q∨R(Q→R)⟹¬P∨Q(P→Q)
- 消解反演
消解通过反演来证明。将目标公式否定添加到命题公式集中,从中推导出一个空子句。(类似于反证法,否定结论,并将其作为条件,推导出一个空结论,即不可能满足的结论)
反演树的画法与理解
- 置换与合一的概念
置换: σ = { f ( a ) / x , f ( y ) / z } \sigma = \{f(a) / x , f(y) / z\} σ={f(a)/x,f(y)/z} 代表用 f ( a ) f(a) f(a)代替掉 x x x,用 f ( y ) f(y) f(y)代替掉 z z z。
合一:寻找一个置换,使两个表达式一致的过程。
3.4 规则演绎
- 产生式系统
产生式规则一般形式:
I F A 1 , A 2 , . . . , A n T H E N B IF \hspace{1em} A_1,A_2,...,A_n \hspace{1em} THEN \hspace{1em} B IFA1,A2,...,AnTHENB
逻辑蕴含式是产生式的一种特殊形式。
产生式系统的组成:
- 总数据库
- 产生式规则(规则库)
- 控制策略(推理机)
产生式系统的推理:正向推理,逆向推理,双向推理。
3.5 不确定性推理
三种不确定性程度:
- 知识不确定性
- 证据不确定性
- 结论不确定性
不确定性表示度量:
- 静态强度:知识的不确定性程度表示,(LS,LN)为知识的不确定性表示。
- 动态强度:证据的不确定性程度表示
3.5.1 ⭐️概率推理
条件概率公式:
P
(
A
∣
B
)
=
P
(
A
B
)
P
(
B
)
P(A|B) = \frac{P(AB)}{P(B)}
P(A∣B)=P(B)P(AB)
全概率公式:(
A
i
A_i
Ai构成一个完备事件组,互相独立,其总和为全集)
P
(
B
)
=
∑
i
=
1
n
P
(
A
i
)
P
(
B
∣
A
i
)
P(B) = \sum \limits_{i = 1}^n P(A_i)P(B|A_i)
P(B)=i=1∑nP(Ai)P(B∣Ai)
贝叶斯公式:(先验概率
P
(
H
)
P(H)
P(H),条件概率
P
(
H
∣
E
)
P(H|E)
P(H∣E))
P
(
H
∣
E
)
=
P
(
H
)
P
(
E
∣
H
)
P
(
E
)
P
(
B
i
∣
A
)
=
P
(
B
i
)
P
(
A
∣
B
i
)
∑
i
P
(
B
i
)
P
(
A
∣
B
i
)
P
(
H
i
∣
E
1
E
2
⋯
E
m
)
=
P
(
E
1
∣
H
i
)
P
(
E
2
∣
H
i
)
⋯
P
(
E
m
∣
H
i
)
P
(
H
i
)
∑
j
=
1
n
P
(
E
1
∣
H
j
)
P
(
E
2
∣
H
j
)
⋯
P
(
E
m
∣
H
j
)
P
(
H
j
)
P(H|E) = \frac{P(H)P(E|H)}{P(E)} \\ P(B_i | A) = \frac{P(B_i)P(A|B_i)}{\sum_i P(B_i) P(A|B_i)} \\ P(H_i | E_1E_2 \cdots E_m) = \frac{P(E_1|H_i)P(E_2|H_i) \cdots P(E_m|H_i)P(H_i)}{\sum \limits_{j = 1}^n P(E_1|H_j)P(E_2|H_j) \cdots P(E_m|H_j)P(H_j)}
P(H∣E)=P(E)P(H)P(E∣H)P(Bi∣A)=∑iP(Bi)P(A∣Bi)P(Bi)P(A∣Bi)P(Hi∣E1E2⋯Em)=j=1∑nP(E1∣Hj)P(E2∣Hj)⋯P(Em∣Hj)P(Hj)P(E1∣Hi)P(E2∣Hi)⋯P(Em∣Hi)P(Hi)

3.5.2 ⭐️ 主观贝叶斯(?我们是没有考,但是你们就不一定了)

相关公式:
O
(
X
)
=
P
(
X
)
1
−
P
(
X
)
O
(
H
∣
E
)
=
L
S
⋅
O
(
H
)
O
(
H
∣
¬
E
)
=
L
N
⋅
O
(
H
)
O
(
H
∣
S
1
,
S
2
,
⋯
,
S
n
)
=
O
(
H
∣
S
1
)
O
(
H
)
⋅
O
(
H
∣
S
2
)
O
(
H
)
⋯
O
(
H
∣
S
n
)
O
(
H
)
⋅
O
(
H
)
O(X) = \frac{P(X)}{1 - P(X)} \\ O(H|E) = LS \cdot O(H) \\ O(H| \neg E) = LN \cdot O(H) \\ O(H|S_1, S_2, \cdots, S_n) = \frac{O(H|S_1)}{O(H)} \cdot \frac{O(H|S_2)}{O(H)} \cdots \frac{O(H|S_n)}{O(H)} \cdot O(H)
O(X)=1−P(X)P(X)O(H∣E)=LS⋅O(H)O(H∣¬E)=LN⋅O(H)O(H∣S1,S2,⋯,Sn)=O(H)O(H∣S1)⋅O(H)O(H∣S2)⋯O(H)O(H∣Sn)⋅O(H)

EH公式:
P
(
H
∣
S
)
=
{
P
(
H
∣
¬
E
)
+
P
(
H
)
−
P
(
H
∣
¬
E
)
P
(
E
)
×
P
(
E
∣
S
)
0
≤
P
(
E
∣
S
)
<
P
(
E
)
P
(
H
)
+
P
(
H
∣
E
)
−
P
(
H
)
1
−
P
(
E
)
×
(
P
(
E
∣
S
)
−
P
(
E
)
)
P
(
E
)
≤
P
(
E
∣
S
)
≤
1
(
1
)
P(H|S) = \begin{cases} P(H| \neg E) + \frac{P(H) - P(H|\neg E)}{P(E)} \times P(E|S) & 0 \le P(E|S) \lt P(E) \\ P(H) + \frac{P(H|E) - P(H)}{1 - P(E)} \times (P(E|S) - P(E)) & P(E) \le P(E|S) \le 1 \end{cases} \hspace{2em} (1)
P(H∣S)={P(H∣¬E)+P(E)P(H)−P(H∣¬E)×P(E∣S)P(H)+1−P(E)P(H∣E)−P(H)×(P(E∣S)−P(E))0≤P(E∣S)<P(E)P(E)≤P(E∣S)≤1(1)
CP公式:
P
(
H
∣
S
)
=
{
P
(
H
∣
¬
E
)
+
(
P
(
H
)
−
P
(
H
∣
¬
E
)
)
×
(
1
5
C
(
E
∣
S
)
+
1
)
C
(
E
∣
S
)
≤
0
P
(
H
)
+
(
P
(
H
∣
E
)
−
P
(
H
)
)
×
1
5
C
(
E
∣
S
)
C
(
E
∣
S
)
>
0
(
2
)
P(H|S) = \begin{cases} P(H| \neg E) + (P(H) - P(H|\neg E)) \times (\frac{1}{5}C(E|S) + 1) & C(E|S) \le 0 \\ P(H) + (P(H|E) - P(H)) \times \frac{1}{5}C(E|S) & C(E|S) \gt 0 \end{cases} \hspace{2em} (2)
P(H∣S)={P(H∣¬E)+(P(H)−P(H∣¬E))×(51C(E∣S)+1)P(H)+(P(H∣E)−P(H))×51C(E∣S)C(E∣S)≤0C(E∣S)>0(2)
根据第一张图得到 P ( E ∣ S ) P(E|S) P(E∣S)与 C ( E ∣ S ) C(E|S) C(E∣S)的关系,记为式 ( 3 ) (3) (3)
根据第二张图得到 P ( H ∣ S ) P(H|S) P(H∣S)与 P ( E ∣ S ) P(E|S) P(E∣S)的关系,即为式 ( 1 ) (1) (1)
将式 ( 3 ) (3) (3)代入到式 ( 1 ) (1) (1)中,得到CP公式

3.5.3 ⭐️可信度方法
可信度表示知识或证据的不确定性,范围 [ − 1 , 1 ] [-1,1] [−1,1]
知识的不确定性表示:
if E then H (CF(H, E))
CF(H,E):是该条知识的可信度,称为可信度因子或规则强度,它指出当前提条件 E 所对应的证据为真时,它对结论为真的支持程度。


推理结论CF值计算:
C
F
(
H
)
=
C
F
(
H
,
E
)
×
m
a
x
{
0
,
C
F
(
E
)
}
CF(H) = CF(H, E) \times max\{0, CF(E) \}
CF(H)=CF(H,E)×max{0,CF(E)}
重复结论CF值计算:
i
f
E
1
t
h
e
n
H
(
C
F
(
H
,
E
1
)
)
i
f
E
2
t
h
e
n
H
(
C
F
(
H
,
E
2
)
)
则
C
F
1
,
2
(
H
)
=
{
C
F
1
(
H
)
+
C
F
2
(
H
)
−
C
F
1
(
H
)
×
C
F
2
(
H
)
C
F
1
(
H
)
≥
0
,
C
F
2
(
H
)
≥
0
C
F
1
(
H
)
+
C
F
2
(
H
)
+
C
F
1
(
H
)
×
C
F
2
(
H
)
C
F
1
(
H
)
<
0
,
C
F
2
(
H
)
<
0
C
F
1
(
H
)
+
C
F
2
(
H
)
1
−
m
i
n
{
∣
C
F
1
(
H
)
∣
,
∣
C
F
2
(
H
)
∣
}
C
F
1
(
H
)
,
C
F
2
(
H
)
异号
if \hspace{1em} E_1 \hspace{1em} then \hspace{1em} H \hspace{1em} (CF(H,E_1)) \\ if \hspace{1em} E_2 \hspace{1em} then \hspace{1em} H \hspace{1em} (CF(H,E_2)) \\ \text{则} CF_{1,2}(H) = \begin{cases} CF_1(H) + CF_2(H) - CF_1(H) \times CF_2(H) & CF_1(H) \ge 0, CF_2(H) \ge 0 \\ CF_1(H) + CF_2(H) + CF_1(H) \times CF_2(H) & CF_1(H) \lt 0, CF_2(H) \lt 0 \\ \frac{CF_1(H) + CF_2(H)}{1 - min\{ |CF_1(H)|, |CF_2(H)|\}} & CF_1(H),CF_2(H) \text{异号} \end{cases}
ifE1thenH(CF(H,E1))ifE2thenH(CF(H,E2))则CF1,2(H)=⎩
⎨
⎧CF1(H)+CF2(H)−CF1(H)×CF2(H)CF1(H)+CF2(H)+CF1(H)×CF2(H)1−min{∣CF1(H)∣,∣CF2(H)∣}CF1(H)+CF2(H)CF1(H)≥0,CF2(H)≥0CF1(H)<0,CF2(H)<0CF1(H),CF2(H)异号

4 计算智能
4.1 神经计算
神经网络三要素:
-
神经元
- 为一个简单的线性阈值单元(阈值逻辑单元TLU),简单的单层前馈网络,叫感知器
- 多个输入通过 f ( ∑ i = 1 n w i x i − θ ) f(\sum \limits_{i = 1}^n w_i x_i - \theta) f(i=1∑nwixi−θ)输出, f f f称为变换函数, θ \theta θ称为阈值或偏差。
-
网络拓扑结构
- 递归(反馈)网络(多个神经元之间组成一个互连神经网络)
- 前馈(多层)网络(神经元之间不存在互连)(代表:BP网络(梯度下降法))
-
学习算法
-
有师学习算法
-
无师学习算法(无需知道期望输出)
- 聚类算法
-
强化学习算法
- 遗传算法
-
感知器逻辑推理:
- 可以解决
AND, OR, NOT问题 - 不可解决线性不可分问题,例如
XOR问题 - 但XOR可以使用多层感知器网络(前馈网络)和递归网络实现
4.2 模糊计算
4.2.1 表示
A = { ( x , μ A ( x ) ) ∣ x ∈ U } A = \{ (x, \mu_A(x)) |x \in U \} A={(x,μA(x))∣x∈U}
μ A ( x ) \mu_A(x) μA(x) : x x x对 A A A的隶属度, μ A ( x ) ∈ [ 0 , 1 ] \mu_A(x) \in [0, 1] μA(x)∈[0,1]
表示:
-
X X X为离散域
F = ∑ i = 1 n μ F ( x ) / x A = 0 / 1 + 0.1 / 2 + 0.5 / 3 + 0.8 / 4 + 1 / 5 或 F = { μ F ( u 1 ) , μ F ( u 2 ) , ⋯ , μ F ( u n ) } A = { 0 , 0.1 , 0.5 , 0.8 , 1 } F = \sum \limits_{i = 1}^n \mu _F(x) / x \hspace{1em} A = 0/1 + 0.1/2 + 0.5/3 + 0.8 / 4 + 1/5 \\ \text{或} \\ F = \{\mu_F(u_1), \mu_F(u_2), \cdots, \mu_F(u_n) \} \hspace{1em} A = \{0, 0.1, 0.5, 0.8, 1 \} F=i=1∑nμF(x)/xA=0/1+0.1/2+0.5/3+0.8/4+1/5或F={μF(u1),μF(u2),⋯,μF(un)}A={0,0.1,0.5,0.8,1} -
X X X 为连续域
F = ∫ X μ F ( x ) / x F = \int_X \mu_F(x) / x F=∫XμF(x)/x
4.2.2 模糊运算

4.2.3 原理(求解过程)
- 模糊化
- 模糊计算:模糊统计法,对比排序法,专家评判法
- 模糊判决(解模糊):重心法,最大隶属度法,系统加权平均法,隶属度限幅元素平均法
4.3 ⭐️遗传算法
- 是一种模仿生物遗传学和自然选择机理的优化搜索算法,是进化计算的一种重要的形式。有选择算子,交叉算子,变异算子。
- 流程
- 初始化群体,群体中的每一个个体都是染色体,由二进制串组成,所以算法中会牵扯到编码和解码操作
- 计算所有个体的适应度(适应度函数由用户自定义,保证适应度大的个体质量更好)
- 选择:选择方法一般有赌轮选择和联赛选择。赌轮选择:每个个体有一个选择的概率,可以定为个体的适应度除以群体总的适应度,产生随机数选择一个个体。联赛选择:随机选择m个个体,选择适应度最大的个体。选择之后要进行解码操作。
- 以某一概率进行交叉。(交叉分为一点交叉和两点交叉)
- 以某一概率进行突变
- 直至满足某种停止条件,否则一直进行适应度计算往下的操作
- 输出适应度最优的染色体作为最优解
4.4 ⭐️粒群优化算法(? 什么东西,我们是没考,这个重点感觉就是烟雾弹)
迭代公式
速度更新公式:
v
(
t
+
1
)
=
w
v
(
t
)
+
c
1
r
a
n
d
(
)
(
p
i
−
x
(
t
)
)
+
c
2
r
a
n
d
(
)
(
p
g
−
x
(
t
)
)
v(t + 1) = wv(t) + c_1rand() (p_i - x(t)) + c_2rand()(p_g - x(t))
v(t+1)=wv(t)+c1rand()(pi−x(t))+c2rand()(pg−x(t))
w w w :惯性权重, c 1 , c 2 c_1,c_2 c1,c2 :加速常数, p i p_i pi :个体极值, p g p_g pg :全局极值
位置更新公式: x ( t + 1 ) = x ( t ) + v ( t + 1 ) x(t + 1) = x(t) + v(t + 1) x(t+1)=x(t)+v(t+1)
5 机器学习
5.1 归纳学习
分为:
- 有师学习(示例学习)
- 无师学习(观察发现学习)
5.2 神经网络学习
BP算法:反向传播算法
学习过程:正向传播 + 反向传播
5.3 深度学习
定义:将神经-中枢-大脑的工作原理设计成一个不断迭代、不断抽象的过程,以便得到最优数据特征表示的机器学习算法
卷积神经网络:
- 神经元之间非全连接
- 同一层神经元之间采用权值共享的方式
优点:
- 采用非线性处理单元组成的多层结构
- 分为有监督学习和无监督学习
- 学习无标签数据优势明显
常用模型:
- 自动编码器:无监督学习
- 受限玻尔兹曼机:学习概率分布的一个随机生成神经网络,限定模型必须为二分图
- 深度信念网络:靠近可视层部分使用贝叶斯信念网络
- 卷积神经网络:多个卷积层和全连接层组成
5.4 ⭐️决策树
可参考:https://wyqz.top/p/808139430.html#toc-heading-34
信息熵:
E
n
t
(
X
)
=
−
∑
p
i
l
o
g
2
p
i
i = 1, 2,
…
, n
Ent(X) = - \sum p_i log_2 p_i \hspace{2em} \text{i = 1, 2, …, n}
Ent(X)=−∑pilog2pii = 1, 2, …, n
信息增益: 表示特征
X
X
X使得类
Y
Y
Y的不确定性减少的程度(熵值减少),即当前划分对信息熵所造成的变化。
信息增益越大,表示特征a来划分所减少的熵最大,即提升最大,应当作为根节点。
G
a
i
n
(
S
,
A
)
=
E
n
t
(
S
)
−
∑
v
∈
v
a
l
u
e
s
(
A
)
∣
S
v
∣
∣
S
∣
E
n
t
(
S
v
)
Gain(S, A) = Ent(S) - \sum \limits_{v \in values(A)} \frac{|S_v|}{|S|} Ent(S_v)
Gain(S,A)=Ent(S)−v∈values(A)∑∣S∣∣Sv∣Ent(Sv)
基于信息增益的ID3算法的实例:
我们有14天的数据,4个特征条件:天气,温度,湿度,是否有风。最终结果是去玩不玩。


上面有四种划分方式,我们需要判断谁来当根节点,根据的主要就是信息增益这个指标。下面计算信息增益来判断根节点。
总的数据中,9天玩,5天不玩,熵值为:
−
9
14
l
o
g
2
9
14
−
5
14
l
o
g
2
5
14
=
0.940
-\frac{9}{14}log_2 \frac{9}{14} - \frac{5}{14}log_2 \frac{5}{14} = 0.940
−149log2149−145log2145=0.940
本例暂且以ent(a, b)代表以下含义:(只有两种结果的时候的熵值计算)
from math import log2
def ent(a, b):
tot = a + b
x, y = a / tot, b / tot
return -(x * log2(x) + y * log2(y))
然后对4个特征逐个分析:
-
outlook
-
outlook = sunny时,熵值为0.971,取值为sunny的概率为 5 14 \frac{5}{14} 145 -
outlook = overcast时,熵值为0,取值为overcast的概率为 4 14 \frac{4}{14} 144 -
outlook = rainy时,熵值为0.971,取值为rainy的概率为 5 14 \frac{5}{14} 145
熵值为:
5 14 × 0.971 + 4 14 × 0 + 5 14 × 0.971 = 0.693 \frac{5}{14} \times 0.971 + \frac{4}{14} \times 0 + \frac{5}{14} \times 0.971 = 0.693 145×0.971+144×0+145×0.971=0.693
信息增益:系统熵值从0.940下降到0.693,增益为0.247。 -
-
temperture
-
temperture = hot时,熵值为1.0(ent(2, 2)),取值为hot的概率为 4 14 \frac{4}{14} 144 -
temperture = mild时,熵值为0.918(ent(4, 2)),取值为mild的概率为 6 14 \frac{6}{14} 146 -
temperture = cool时,熵值为0.81(ent(3,1)),取值为cool的概率为 4 14 \frac{4}{14} 144
熵值为:
4 14 × 1.0 + 6 14 × 0.918 + 4 14 × 0.81 = 0.911 \frac{4}{14} \times 1.0 + \frac{6}{14} \times 0.918 + \frac{4}{14} \times 0.81 = 0.911 144×1.0+146×0.918+144×0.81=0.911
信息增益: G a i n ( S , t e m p e r t u r e ) = 0.940 − 0.911 = 0.029 Gain(S, temperture) = 0.940 - 0.911 = 0.029 Gain(S,temperture)=0.940−0.911=0.029 -
G a i n ( S , O u t l o o k ) = 0.247 G a i n ( S , H u m i d i t y ) = 0.151 G a i n ( S , W i n d ) = 0.048 G a i n ( S , T e m p e r a t u r e ) = 0.029 Gain(S,Outlook)=0.247 \\ Gain(S, Humidity)=0.151 \\ Gain(S, Wind)=0 .048 \\ Gain(S,Temperature)=0 .029 Gain(S,Outlook)=0.247Gain(S,Humidity)=0.151Gain(S,Wind)=0.048Gain(S,Temperature)=0.029
计算出所有的信息增益之后,选择有最大的信息增益的特征作为根节点。
下面找Sunny分支的决策树划分:
总的熵值
−
2
5
×
l
o
g
2
(
2
5
)
−
3
5
l
o
g
2
(
3
5
)
=
0.97
-\frac{2}{5} \times log_2(\frac{2}{5}) - \frac{3}{5}log_2(\frac{3}{5}) = 0.97
−52×log2(52)−53log2(53)=0.97
以剩下的三个特征进行分析:
-
temperture
- temperture=hot,熵值为0,概率为 2 5 \frac{2}{5} 52
- temperture=mild,熵值为1.0,概率为 2 5 \frac{2}{5} 52
- temperture=cool,熵值为0,概率为 1 5 \frac{1}{5} 51
熵值为 2 5 \frac{2}{5} 52
信息增益: 0.97 − 0.4 = 0.57 0.97-0.4 = 0.57 0.97−0.4=0.57
-
humidity
- high,熵值为0,概率为 3 5 \frac{3}{5} 53
- normal,熵值为1,概率为 2 5 \frac{2}{5} 52
熵值为 2 5 \frac{2}{5} 52
信息增益: 0.97 − 0.4 = 0.57 0.97 - 0.4 = 0.57 0.97−0.4=0.57
-
windy
- false,熵值为0.918,概率为 3 5 \frac{3}{5} 53
- true,熵值为1,概率为 2 5 \frac{2}{5} 52
熵值为 0.951 0.951 0.951
信息增益: 0.97 − 0.95 = 0.02 0.97 - 0.95 = 0.02 0.97−0.95=0.02
故选择humidy或temperture划分
剩下的划分同理
最终决策树:文章来源:https://www.toymoban.com/news/detail-469276.html
 文章来源地址https://www.toymoban.com/news/detail-469276.html
文章来源地址https://www.toymoban.com/news/detail-469276.html
到了这里,关于人工智能及其应用(蔡自兴)期末复习的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!