C语言完整代码实现：二叉树的先序遍历、中序遍历、后序遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了C语言完整代码实现：二叉树的先序遍历、中序遍历、后序遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、先序遍历原理

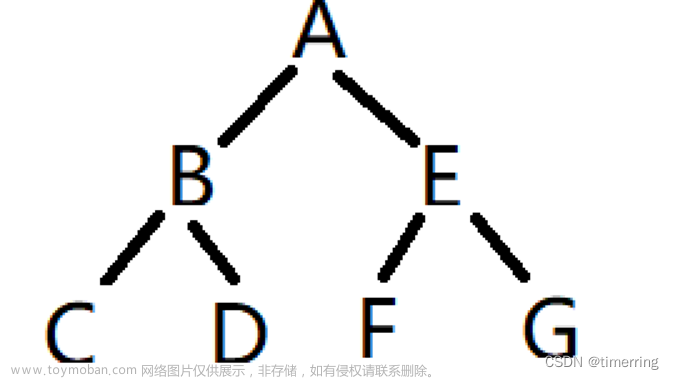
先序遍历就是：根、左、右，也就是先遍历根结点再遍历左结点最后再遍历右结点，注意：如果遍历到的结点不是叶子结点的话需要对该结点进行拆分，比如这棵二叉树：

C语言完整代码实现：二叉树的先序遍历、中序遍历、后序遍历

先遍历A，然后是B，然后再是C，但是由于B并不是叶子结点，他本身又是一棵子树的根结点，所以B可以拆分成B、D、E（根、左、右），同理因为C本身又是一棵子树的根结点根据先序遍历的原则C也可以拆分为C、F（根、左、右），然后再组合在一起便是A、B、D、E、C、F，此时D还不是叶子结点，同理再将D进行拆分为D、G（根左右），最后得到A、B、D、G、E、C、F。如下图所示

C语言完整代码实现：二叉树的先序遍历、中序遍历、后序遍历

二、代码实现

通过上面的分析我们可以通过递归来实现树的遍历

1、先序遍历

void preOrder(BiTree T){
    if(T != NULL){
        visit(T);//先访问根节点
        preOrder(T->lchild);//再访问左结点
        preOrder(T->rchild);//最后访问右结点
    }
    return;
}

2、中序遍历

void midOrder(BiTree T){
    if(T != NULL){
        midOrder(T->lchild);//先访问左结点
        visit(T);//再访问根结点
        midOrder(T->rchild);//最后访问右结点
    }
    return;
}

3、后序遍历

void lastOrder(BiTree T){
    if(T != NULL){
        lastOrder(T->lchild);//先访问左结点
        lastOrder(T->rchild);//再访问右结点
        visit(T);//最后访问根节点
    }
    return;
}

其中visit函数就是打印访问到的结点，xxxOrder函数就是一个递归函数，如果T已经是叶子结点了，那么就会返回，如果T是分支结点，也就是说还有左孩子或右孩子的话那么就访问对应的左孩子或右孩子，直到为叶子结点再返回，可以理解为上面讲的拆分（剥开）的原理，其实也就是递归的原理。

4、完整代码实现

#include <stdio.h>
#include <stdlib.h>
typedef struct BiTNode{
    char data;
    struct BiTNode *lchild, *rchild;
}BiTNode,*BiTree;
//初始化根节点
BiTree init_Tree(BiTree T){
      //创建根节点，让指针T指向根节点
      T = (BiTree)malloc(sizeof(struct BiTNode));
      T->data = 'A';
      T->lchild = NULL;
      T->rchild = NULL;
      return T;
}
BiTree insert_Tree_left(BiTree Tree,char ch){
     BiTree p = (BiTree) malloc(sizeof(struct BiTNode));
     p->lchild = NULL;
     p->rchild = NULL;
     p->data = ch;
     Tree->lchild = p;
     return p;
}
BiTree insert_Tree_right(BiTree Tree,char ch){
    BiTree p = (BiTree) malloc(sizeof(struct BiTNode));
    p->lchild = NULL;
    p->rchild = NULL;
    p->data = ch;
    Tree->rchild = p;
    return p;
}
//访问对应的结点的值
void visit(BiTree tree){
    printf("%c ",tree->data);
    return;
}

//树的先序遍历
void preOrder(BiTree T){
    if(T != NULL){
        visit(T);//先访问根节点
        preOrder(T->lchild);//再访问左结点
        preOrder(T->rchild);//最后访问右结点
    }
    return;
}
//中序遍历
void midOrder(BiTree T){
    if(T != NULL){
        midOrder(T->lchild);//先访问左结点
        visit(T);//再访问根结点
        midOrder(T->rchild);//最后访问右结点
    }
    return;
}
void lastOrder(BiTree T){
    if(T != NULL){
        lastOrder(T->lchild);//先访问左结点
        lastOrder(T->rchild);//再访问右结点
        visit(T);//最后访问根节点
    }
    return;
}
int main() {
    BiTree T = NULL;
    T = init_Tree(T);
    BiTree B = insert_Tree_left(T,'B');
    BiTree C = insert_Tree_right(T,'C');

    BiTree D = insert_Tree_left(B,'D');
    BiTree E = insert_Tree_right(B,'E');

    insert_Tree_right(D,'G');
    insert_Tree_left(C,'F');
    printf("先序遍历：");
    preOrder(T);
    printf("\n");
    printf("中序遍历：");
    midOrder(T);
    printf("\n");
    printf("后序遍历：");
    lastOrder(T);
    return 0;
}

5、运行结果

C语言完整代码实现：二叉树的先序遍历、中序遍历、后序遍历