最小生成树是一个连通图。什么是连通图,(强)连通图详解前面介绍了《图存储结构》,本节继续讲解什么是 连通图 。 前面讲过,图中从一个顶点到达另一顶点,若存在至少一条路径,则称这两个顶点是连通着的。例如图 1 中,虽然 V1 和 V3http://c.biancheng.net/view/3405.html
Kruskal算法的图形分析:
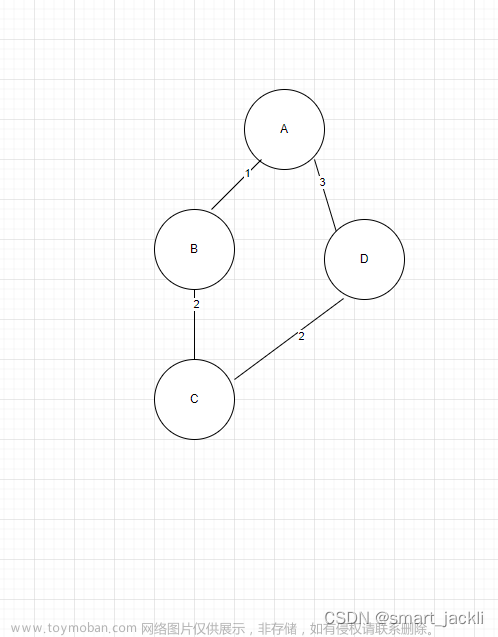
从下面的有权图中找出最小生成树:Kruskal算法是一种贪心算法,也是取边法,首先取出权值最小的边AC,再在剩下的边中依次取出权值最小却不会形成环的边。

①取出AC

②取出AB或者AD

③取出AB或者AD剩下的一个,上面取了AB,则取AD

④再下来最下的权值是边BC或者CD的权值为3,但当加入其中一条边回形成环,不满足,舍去,接着往下找剩下权值最小的边

⑤取出AE或者BE其中一条(直到这里就完成了,边数n为顶点数减1),这里你把AE边换成BE边也是可以的,所以说最小长生树不唯一

Kruskal算法的核心步骤:
①、权值从小到大进行排序
②、比较根结点是否相同(判断是否形成环)
对第②点进行解释一下,用辅助数组来记录每个顶点的根结点,一开始他们都是独立的一棵树,根结点是自己本身,初始值如下

当加入第一条权值最小边AC时,将终点顶点C看成时开始点顶点A的孩子,也就是C的根结点由原来指向自己到现在指向A,值由原来的2更新为0

加入第二条权值最小的边AB,B的根结点值更新为0

加入第三条权值最小的边AD,D的根结点值更新为0

在加入第四条权值最小的边BC或者CD时,其中B和C的根结点都是0,或者C和D的根结点值都是0,形成了环,所以舍去,依次下去,直到形成最小生成树为止。

接下来就是代码了:
红色方框时核心的算法

排序前的边集数组:(根据输入的顺序)

进行排序后的边集数组:

文章来源地址https://www.toymoban.com/news/detail-469851.html文章来源:https://www.toymoban.com/news/detail-469851.html
到了这里,关于Kruskal算法求解最小生成树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!