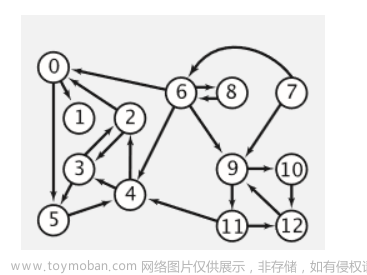
拓扑序一定是有向无环图。
拓扑排序不唯一


拓扑排序方法一:
利用入度为零进行排序
思路:谁的入度为0,谁就是开始节点,将开始节点打印完之后,将开始节点的直接邻居的入度减1,然后重复。

package algorithmbasic.class17;
import java.util.*;
//图的拓扑排序
public class TopologySort {
public static List<Node> sortedTopology(Graph graph) {
//result用来盛放排序结果。
List<Node> result = new ArrayList<>();
//inmap存放节点与入度的对应值。
//key ——> 某个节点, value ——> 剩余入度
HashMap<Node, Integer> inmap = new HashMap<>();
//只有节点的入度为0才可以进入此队列。
Queue<Node> inZeroQueue = new LinkedList<>();
for (Node node : graph.nodes.values()) {
inmap.put(node, node.in);
if (node.in == 0) {
inZeroQueue.add(node);
}
}
Node cur = inZeroQueue.poll();
result.add(cur);
for (Node next : cur.nexts) {
//剩余入度减1.
inmap.put(next, inmap.get(next) - 1);
if (inmap.get(next) == 0) {
inZeroQueue.add(next);
}
}
return result;
}
}
拓扑排序方法二:
利用点次进行排序。

点次越大的,排序位置越靠前。
而且我发现可以使用递归进行求点次。我们要求0的点次,那就需要求他的直接邻居1,2,3的点次,然后对邻居的点次求和再加1,就是0的点次。我们可以将每个点的点次放在一个表里面,这个表记录着哪个节点的点次对应着多少。这样我们再求其他节点点次时直接从表里拿就行,减少重复性工作。
思路:
1:创建一个表 HashMap<DirectedGraphNode, Record> order = new HashMap<>() 用来记录每个节点对应的点次是多少。2:遍历整个图中的每一个节点,记录其点次。
3:创建一个有序表ArrayList records = new ArrayList<>() 用来记录点次。
4:根据点次进行由大到小的排序。records.sort(new MyComparator());
5:然后再创建一个有序表ArrayList dnodes = new ArrayList<>() 根据点次的顺序记录节点。
注意为什么要创建Record这个内部类。因为在 “ 根据点次的顺序记录节点” 时,我们需要根据点次找到对应的节点,使用map是不可以的,因为点次大小有重复的。所以我们采用内部类的方法,这样每个点次都会有一一对应的节点。
package algorithmbasic.class17;
//图的拓扑排序方法二
import java.util.*;
// OJ链接:https://www.lintcode.com/problem/topological-sorting
public class TopologicalOrderDFS2 {
/**
* 节点内部类
*/
// 不要提交这个类
public static class DirectedGraphNode {
public int label;
public ArrayList<DirectedGraphNode> neighbors;
public DirectedGraphNode(int x) {
label = x;
neighbors = new ArrayList<DirectedGraphNode>();
}
}
/**
* 点次内部类。
*/
//记录某个节点的点次。
public static class Record {
public DirectedGraphNode node;
//点次。
public long nodes;
public Record(DirectedGraphNode node, long nodes) {
this.node = node;
this.nodes = nodes;
}
}
/**
* topSort方法
* 传入一张图的所有节点,返回排序好后的所有节点。
*/
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
//采用计算每个节点点次的方法。
//建立一张表用来记录每个节点对应的点次是多少。
HashMap<DirectedGraphNode, Record> order = new HashMap<>();
ArrayList<Record> records = new ArrayList<>();
ArrayList<DirectedGraphNode> dnodes = new ArrayList<>();
//遍历图中每个节点,并记录每个节点出现的点次。
for (DirectedGraphNode cur : graph) {
Record record = process(cur, order);
records.add(record);
//order.put(cur, record);
}
//Arrays.sort(records,new MyComparator());
records.sort(new MyComparator());
for (Record r : records) {
dnodes.add(r.node);//这就是为什么要建立Record这个内部类的原因。
}
return dnodes;
}
/**
* 求点次的方法。
*/
//传入一个节点返回这个节点的点次。在递归的过程当中每个节点的点次其实都已经记录好了。
public static Record process(DirectedGraphNode node, HashMap<DirectedGraphNode, Record> order) {
if (order.containsKey(node)) {
return order.get(node);
}
//order中没有该点。
long count = 0;
for (DirectedGraphNode n : node.neighbors) {
Record r = process(n, order);
count += r.nodes;
}
Record record = new Record(node, count + 1);
//先把当前节点及其点次放入map中然后再返回。这样我们再求其他节点点次时直接从表里拿就行,减少重复性工作。
order.put(node, record);
return record;
}
/**
* 比较器
*/
public static class MyComparator implements Comparator<Record> {
@Override
public int compare(Record o1, Record o2) {
//不要将long类型数据强制转换成int类型,会出现溢出和截断的风险,导致数据出现错误。
//例如2147483648L -> int:-2147483648
//它超过了int类型的最大值 2147483647。当将其强制转换为int类型时,结果被截断为int类型的最小值 -2147483648。
//return (int)(o2.nodes - o1.nodes);
return o1.nodes == o2.nodes ? 0 : (o1.nodes > o2.nodes ? -1 : 1);
}
}
}
拓扑排序方法三:
根据深度进行排序
 文章来源:https://www.toymoban.com/news/detail-469899.html
文章来源:https://www.toymoban.com/news/detail-469899.html
package algorithmbasic.class17;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.HashMap;
public class TopologicalOrderDFS1 {
/**
* 节点内部类
*/
public static class DirectedGraphNode {
public int label;
public ArrayList<DirectedGraphNode> neighbors;
public DirectedGraphNode(int x) {
label = x;
neighbors = new ArrayList<DirectedGraphNode>();
}
}
/**
* 深度内部类。
*/
public static class Deep {
public long deep;
public DirectedGraphNode node;
public Deep(long deep, DirectedGraphNode node) {
this.deep = deep;
this.node = node;
}
}
/**
* topSort方法
*/
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
HashMap<DirectedGraphNode, Deep> order = new HashMap<>();
ArrayList<Deep> deeps = new ArrayList<>();
ArrayList<DirectedGraphNode> dNodes = new ArrayList<>();
for (DirectedGraphNode node : graph) {
Deep d = process(node, order);
deeps.add(d);
}
deeps.sort(new MyComparator());
for (Deep d : deeps) {
dNodes.add(d.node);
}
return dNodes;
}
public static Deep process(DirectedGraphNode node, HashMap<DirectedGraphNode, Deep> order) {
if (order.containsKey(node)) {
return order.get(node);
}
long max = Long.MIN_VALUE;
for (DirectedGraphNode n : node.neighbors) {
Deep d = process(n, order);
max = Math.max(max, d.deep);
}
Deep deep = new Deep(max + 1, node);
order.put(node, deep);
return deep;
}
public static class MyComparator implements Comparator<Deep> {
@Override
public int compare(Deep o1, Deep o2) {
return o1.deep == o2.deep ? 0 : (o1.deep > o2.deep ? -1 : 1);
}
}
}
文章来源地址https://www.toymoban.com/news/detail-469899.html
到了这里,关于17.4:图的拓扑排序的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!