- 博主简介：一个爱打游戏的计算机专业学生
- 博主主页： @夏驰和徐策
- 所属专栏：算法设计与分析
5.1.1 树的定义
我的理解：
在计算机科学中，树是一种非线性数据结构，由节点（或称为顶点）和边组成。它是一种层次结构，具有根节点、子节点和父节点的概念。树的定义如下：
1. 根节点（Root）：树的顶部节点，没有父节点，是树的起始点。
2. 节点（Node）：树中的元素，包含一个或多个子节点和一个父节点。
3. 边（Edge）：节点之间的连接线，表示节点之间的关系。
4. 子节点（Children）：一个节点的直接下属节点。
5. 父节点（Parent）：一个节点的直接上属节点。
6. 叶节点（Leaf）：没有子节点的节点，也称为终端节点。
7. 子树（Subtree）：树中的任意节点及其所有后代节点构成的树。
8. 深度（Depth）：从根节点到某个节点的唯一路径的长度，根节点的深度为0。
9. 高度（Height）：树中节点的最大深度。
树的特点是没有环路（无回路），即任意两个节点之间只有一条简单路径。根据节点的连接方式和属性的不同，树可以有不同的类型，例如二叉树、平衡树、二叉搜索树等。
树的应用非常广泛，它在算法、数据结构、图形学、人工智能等领域都有重要的作用。通过树的结构，我们可以组织和管理数据，进行搜索、插入、删除等操作，并且可以表示层次关系和分层结构。
文章来源地址https://www.toymoban.com/news/detail-470544.html
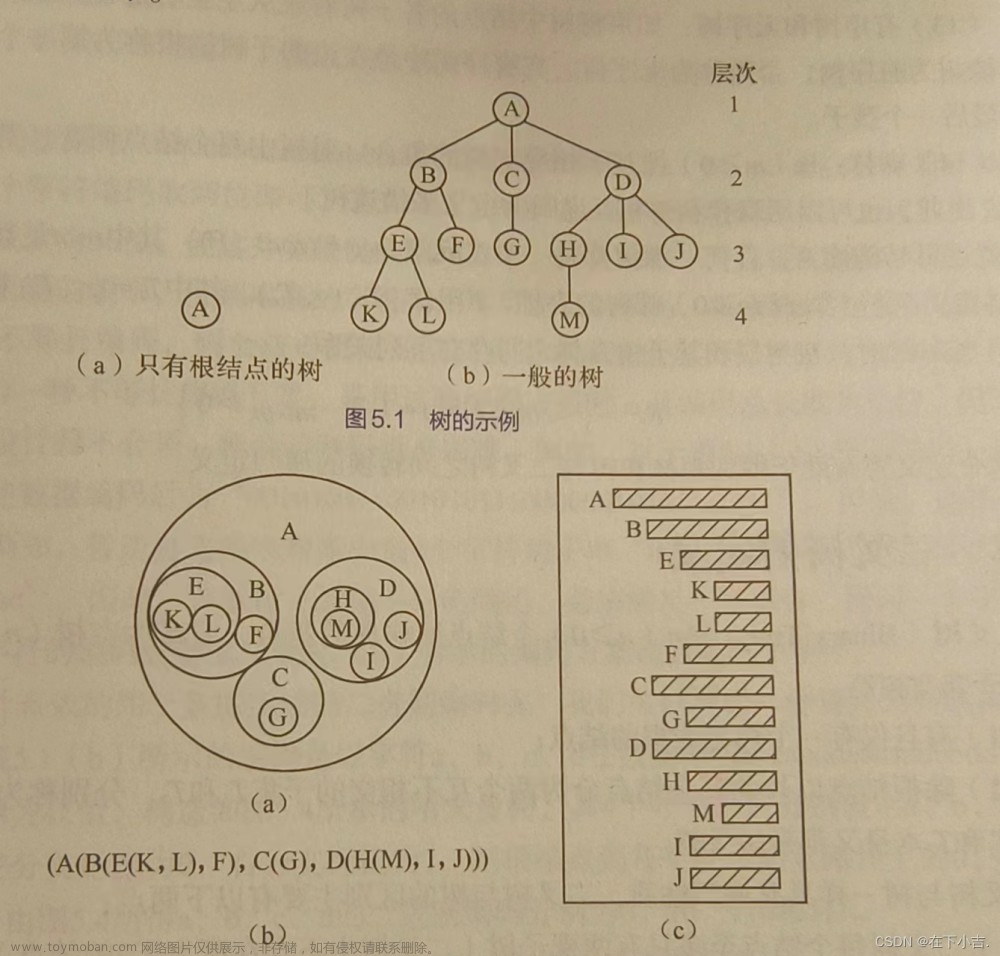
5.1.2 树的基本术语
当涉及到树的讨论时，有一些基本术语被广泛使用。以下是树的基本术语的解释：
1. 节点（Node）：树的基本单元，表示树中的一个元素。每个节点可以包含一个值或其他相关信息。
2. 根节点（Root）：树的顶部节点，它是树的起点，没有父节点。树中只有一个根节点。
3. 叶节点（Leaf）：树中没有子节点的节点，也称为终端节点。叶节点位于树的末端。
4. 父节点（Parent）：一个节点的直接上属节点，位于该节点上方的节点。
5. 子节点（Child）：一个节点的直接下属节点，位于该节点下方的节点。
6. 兄弟节点（Sibling）：具有相同父节点的节点称为兄弟节点。
7. 子树（Subtree）：树中的任意节点及其所有后代节点所构成的子结构被称为子树。子树本身也是一棵树。
8. 祖先节点（Ancestor）：一个节点的所有上属节点，包括父节点、爷爷节点等。
9. 后代节点（Descendant）：一个节点的所有下属节点，包括子节点、孙子节点等。
10. 深度（Depth）：从根节点到某个节点的路径长度，表示该节点在树中的层级关系。根节点的深度为0。
11. 高度（Height）：树中节点的最大深度，表示树的层数。叶节点的高度为0。
12. 森林（Forest）：由多棵树组成的集合称为森林，每棵树都是独立的。
这些基本术语提供了描述树结构的词汇和概念，帮助我们准确地描述树中节点之间的关系和层次结构。理解这些术语将有助于我们在树的操作和应用中进行准确的交流和理解。
5.1.3 二叉树的定义
二叉树是一种特殊的树结构，其中每个节点最多有两个子节点，称为左子节点和右子节点。二叉树的定义如下：
二叉树是由节点集合构成的有限集合，其中每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树可以为空树，即没有节点的情况。
在二叉树中，每个节点最多有两个子节点，可以有零个、一个或两个子节点。这两个子节点的位置是有序的，左子节点位于其父节点的左侧，右子节点位于其父节点的右侧。
二叉树的定义允许节点具有空子节点。当节点没有左子节点或右子节点时，对应的子节点被视为空。如果一个节点既没有左子节点也没有右子节点，那么它就是一个叶节点（叶子）。
需要注意的是，二叉树的定义并没有限定节点的值或其他特定属性，它仅关注节点之间的连接关系和层次结构。二叉树的节点可以携带任意类型的值或附加信息。
二叉树可以具有不同的形状和结构，包括平衡二叉树、完全二叉树、满二叉树等。这些特殊类型的二叉树具有特定的性质和约束条件，可以用于特定的应用场景。
总结：
树是由节点集合构成的一种非线性数据结构，它具有层次结构和分支关系。树的定义如下：
1. 树是一个由节点组成的有限集合。
2. 树中有一个特殊的节点，称为根节点。根节点没有父节点，是树的起始点。
3. 树中的其他节点可以有一个或多个子节点。子节点与父节点之间通过边连接。
4. 每个节点除了根节点外，都有一个唯一的父节点。节点之间通过边相互连接，形成树的结构。
5. 在树中，任意两个节点之间都有唯一的路径连接。
二叉树是一种特殊的树结构，其中每个节点最多有两个子节点，称为左子节点和右子节点。二叉树的定义如下：
1. 二叉树是由节点组成的有限集合。
2. 每个节点最多有两个子节点，分别称为左子节点和右子节点。如果一个节点没有某个子节点，则该子节点被视为空。
3. 二叉树可以为空树，即没有节点的情况。
4. 在二叉树中，节点的左子节点位于其父节点的左侧，右子节点位于其父节点的右侧。
5. 二叉树的节点之间的连接关系是有序的，节点之间没有兄弟关系。
需要注意的是，树和二叉树的定义并没有限定节点的值或其他特定属性，它们仅关注节点之间的连接关系和层次结构。树和二叉树是非常常见且重要的数据结构，在计算机科学和算法设计中有广泛的应用。
文章来源：https://www.toymoban.com/news/detail-470544.html
到了这里，关于5.1 树和二叉树的定义的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
