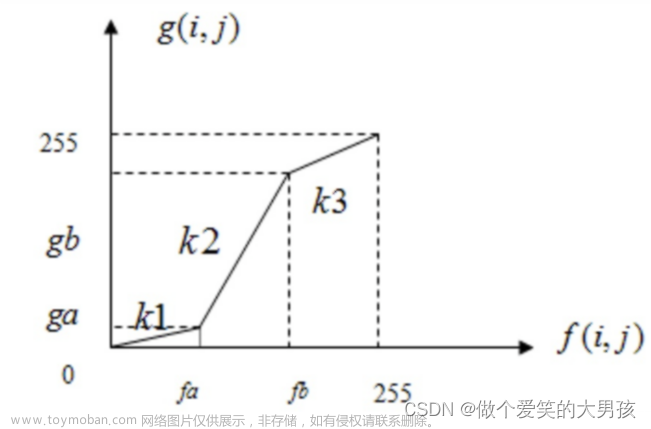
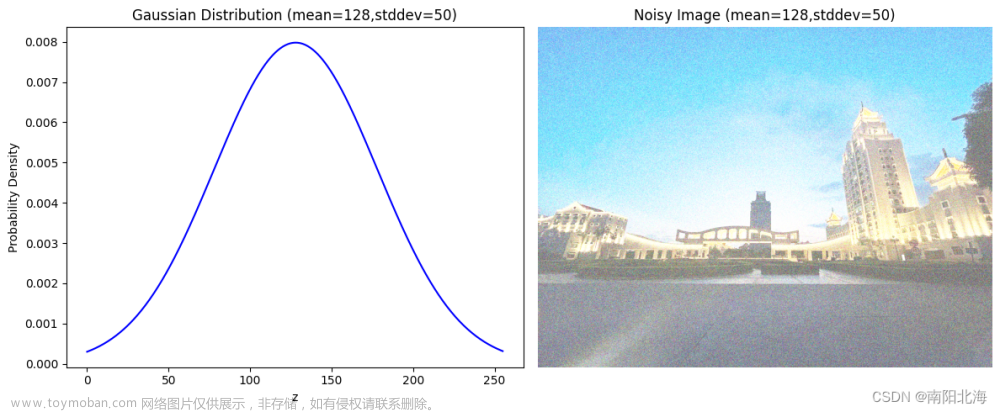
上一篇:数字图像处理考点分析(五) 介绍了图像的形态学处理方法,这一篇我们介绍图像压缩!
图像压缩
1.概念
是什么?
图像压缩:减少表示数字图像所需要的数据量。
为什么图像可以压缩?
- 图像像素之间、⾏之间、帧之间有较 强的相关性
- 从统计的观点,某点像素的灰度与其 邻域灰度有密切关系
- 从信息论关系,减少图像信息中冗余 信息
- 图像数据之所以能被压缩,就是因为数据中存在着冗余,数据压缩的目的就是通过去除这些数据冗余来减少表示数据所需的比特数。
三种数据冗余类型:
1、编码冗余:(编码是用于表示信息实体或事件集合的符号系统(字母、数字、比特和类似的符号等)。每个信息或事件被赋予一个编码符号的序列,称之为码字。每个码字中的符号数量就是该码字的长度。在多数二维灰度阵列中,用于表示灰度的8比特编码所包含的比特数要比表示该灰度所需要的比特数多。 如果编码的码字数大于最佳编码的码字数则就会产生编码冗余
2、空间和时间冗余:因为多数二维灰度阵列的像素是空间相关的(即每一个像素类似于或取决于相邻像素),在相关像素的表示中,信息被没有必要地重复了.在视频序列中,时间相关的像素(即类似于或取决于相邻帧中的那些像素)也是重复的信息。
3、不相关的信息:多数二维灰度阵列中包含有一些被人类视觉系统忽略或与用途无关的信息。从没有被利用的意义上看,它是冗余的。
图像压缩有什么用?
- 节省图像存储容量
- 减少传输信道容量
- 缩短图像加⼯处理时
压缩编码可分为两大类:
-
无损压缩编码
又称为可逆编码(reversible coding),这种方法的目标是在图像没有任何失真的前提下使码率达到最小。
要求编码—解码过程中 能够⽆误差的重建图像。如在医学图像应⽤中。
-
有损压缩编码
又称不可逆压缩(non-reversible coding),这种方法的目标是在给定码率下使图像获得最逼真的视觉效果,或者是在给定的允许图像失真度的条件下使码率到达最小。
常⽤在图像的信宿为⼈ 眼的应⽤中,如数字电视、可视电话等。
特征抽取编码也是一种有损编码,常⽤在图像的信宿为计算机 的应⽤中,这是只需要保留计算机处理的信息 特征。如图像识别。
2. 无损压缩技术
2.1 一些基本概念



熵编码
首先,熵的概念很早就有,在物理学,热力学中早有应用。
后来信息论中,Shannon他老人家发明了信息熵。
公式如下,它代表了信源S的熵:

单位:Bit/字符
**那信息熵到底是什么呢?**它是信息量的度量单位。它的实际意义有两个:
① 信源S的平均信息量
②编码所有符号S平均所需要的位数
为什么要编码? 编码的一个重要目的是压缩 (当然还有其他目的,比如加密)。举个例子就是把100MB的原始数据,压缩成10MB的数据,这个过程就需要编码。
**那么怎么编码才能不失真呢?**就是说解码后可以完全恢复原始数据。用信息熵来计算数据压缩的理论极限呀!
**那什么是熵编码?**在信息熵的极限范围内进行编码就是熵编码。例如信息熵算出来是3bit/字符,你用4bit/字符来编码,就是熵编码,你用2bit/字符来编码,就不叫熵编码,因为这种情况下,就失真了嘛。
从这里也看以看出,信源熵是编码这个信源平均所需要的最小位数。
所以,熵编码是无损压缩。
熵编码有很多种:
-
霍夫曼编码 (Huffman)
-
算术编码
-
行程编码 (RLE)
-
基于上下文的自适应变长编码(CAVLC)
-
基于上下文的自适应二进制算术编码(CABAC)
2.2 Huffman编码
Huffman 压缩编码步骤:
Step1: 把概率按大小从上到下排序;
Step2: 把最下面两个概率相加,再重新排序;
Step3: 重复Step2: ,直到只有两个概率为止;
Step4: 从右向左开始编码。每遇到分叉则在后补位;上叉补0, 下叉补1。(根据题意来看,也有可能是上叉补1,下叉补0)
举例:

计算信息熵H和平均编码长度R:

Huffman编码的特点
- Huffman编码是唯⼀可译码。短的码 不会成为更⻓码的启始部分;
- Huffman编码的平均码⻓接近于熵;
- 缺点:与计算机的数据结构不匹配;
- 缺点:需要多次排序,耗费时间
2.3 香农编码法(Fano-Shannon)
香农编码法步骤

举例:同上题

香农编码的特点
- Fano-Shannon编码是唯⼀可译码。短 的码不会成为更⻓码的启始部分;
- Fano-Shannon编码的平均码⻓接近于 熵;编码效率略低于Huffman编码。
2.4算术编码
思想
-
将被编码的信源消息表示成0~1之间的一个间隔,即小数区间,消息越长,编码表示他的间隔就越小
-
以小数表示间隔,表示的间隔越小所需的二进制位数就越多,码字就越长。反之,间隔越大,码字就短
两种模式
-
基于信源概率统计特性的固定编码模式
-
针对未知信源概率模型的自适应模式
方法
①新子区间的起始位置=前子区间的起始位置+当前符号的区间左端*前子区间长度
②新子区间的结束位置=前子区间的起始位置+当前符号的区间右端*前子区间长度
③将最后的区间化为二进制,去0,把相同部分取出再在末尾加1,即为该数据序列的算术编码
特点
-
算术编码是信息保持型编码,他不像哈夫曼编码,无需为一个符号设定一个码字
-
自适应算术编码的方式,无需先定义概率模型,适合于无法知道信源字符概率分布的情况
-
实现算数编码算法的硬件比哈夫曼编码复杂
举例
一个四符号信源的五符号序列或消息a1,a2,a3,a3,a4进行编码。如下表所示,该区间开始时根据每个信源符号出现的概率被分为4个区域

在编码处理的开始,假设消息占据整个半开区间【0.1)。例如:
符号 a1与子区间【O.0.2)相联系。因为它是被编码的消息的第一个符号,所以该消息间隔开始时被缩窄为【0,0.2)。这样,在下图中,区间【0,0.2)就被扩展到该图形的全高度,且其端点用该窄区间的值来标注。
然后,这个缩窄的区间根据原始信源符号的概率进行细分,并继续对下一个消息符号进行这种处理。采用这种方式,符号 a2将该子区间变窄为【0.04,0.08)。
符号a3进一步将该子区间变窄为【0.056,0.072),依次类推。
必须保留最后的消息符号,以作为特定的消息结束指示符,它将子区间变窄为【0.06752,0.0688)。当然,在这个子区间内的任何数字(如 0.068)都可以用来表示该消息。
感谢CSDN博主【萌萌小刀剑】 的优质文章《数字图像处理》题库5:计算题 ②,使我受益匪浅!文章来源:https://www.toymoban.com/news/detail-470771.html
下一篇:数字图像处理考点分析(七) 我们来介绍图像分割技术!文章来源地址https://www.toymoban.com/news/detail-470771.html
到了这里,关于数字图像处理考点分析(六)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!