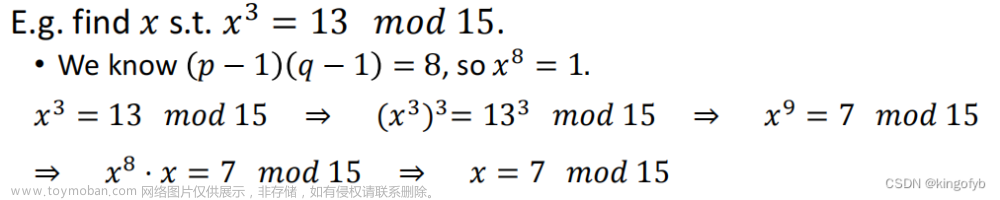文章来源：https://www.toymoban.com/news/detail-471523.html
1. 加密的目的就是传输秘密
2. 分块密码（Block Cipher）的现代加密技术使用了相加把戏的变体
2.1. 加法得出的结果能用于统计分析，这意味着一些人能通过分析你的大量加密消息来得到密钥
2.2. 任何知道密钥的人都能用相反的步骤运行所有操作，以获得最初的、解密的消息
2.3. 最流行的分块密码是高级加密标准（Advanced Encryption Standard）
2.3.1. AES能配合多种不同配置使用，但标准配置是使用16个字母的“块”，配备128位密钥，进行10轮混合操作
3. 单向操作
3.1. One-way Action
3.2. 颜料混合把戏中的单向操作是“混合颜料”
3.3. 可以做一些事情，但不能取消做过的事
4. 混合操作就是离散指数
4.1. Discrete Exponentiation
5. 分离操作被称为离散对数
5.1. Discrete Logarithm
6. 幂函数
6.1. Power Notation
6.2. 写下许多相同数字相乘的快捷方法
6.2.1. 6×6×6×6=6^4
7. 钟算
7.1. Clock Arithmetic
7.2. 钟的大小可以是任何数
7.2.1. 非一座普通的钟上熟悉的12个数字
7.3. 数字从0而不是从1开始计数
7.4. 只能使用比钟大小小的私人数字
7.4.1. 现实中运用时通常会使用几百个数位长的钟大小
7.5. 钟大小必须是一个素数
7.5.1. 只有1和其自身两个除数
7.6. 基数必须是钟大小的本原根（primitive root）
7.6.1. 基数的幂最终将循环遍钟上每个可能的值
7.7. 示例
7.7.1. 用大小为7的钟做钟算，只要像平常一样将数字相加再相除即可，不过不管结果如何，你只要取除以7所得的余数即可
8. 迪菲–赫尔曼密钥交换
8.1. Diffie-Hellman Key Exchange
8.2. 1976年首次发表了这一算法
8.3. 怀特菲德·迪菲（Whitfield Diffie）
8.4. 马丁·赫尔曼（Martin Hellman）
8.5. https:使用的方法是迪菲–赫尔曼机制或工作原理类似的替代方法之一
8.6. 颜料混合把戏（Paint-mixing Trick）
8.6.1. 你和阿诺德各自选择一种“私人颜色”
8.6.2. 选择一种新的不同的颜色成分并公开宣布，我们称这种颜色为“公开颜色”
8.6.3. 你和阿诺德各用一桶公开颜色和一桶私人颜色制造一种混合颜色。这就是你的“公开 – 私人混合颜色”
8.6.4. 你选取一批阿诺德的公开–私人混合颜色，拿回自己的角落。现在加入一桶私人颜色
8.6.5. 阿诺德选取一批你的公开 – 私人混合颜色，拿回他的角落，在那里，他再加入一桶他的私人颜色
8.6.6. 你和阿诺德制作了同样的混合颜色
8.7. 用数字进行颜料混合把戏
8.7.1. 机密信息和公开信息用一种在数学上不可逆的方式“混合”在一起，就像混合在一起的颜料一样，再也分不开
8.8. 共享密钥
8.8.1. 示例
8.8.1.1.
文章来源地址https://www.toymoban.com/news/detail-471523.html
8.8.1.2. 你和阿诺德各自单独选择一个私人数字
8.8.1.2.1. 你选择8作为私人数字，而阿诺德选择9
8.8.1.3. 你和阿诺德公开就两个公开数字达成一致——钟大小（11）和另一个被称为基数的数字（选2为基数）
8.8.1.4. 通过使用幂符号和钟算，你和阿诺德各自将自己的私人数字和公开数字相混，分别得到一个公开–私人数字（public–private number，PPN）
8.8.1.4.1. PPN=base^私人数字（钟大小）
8.8.1.4.2. 你的PPN=（2^8=256，256 mod 11）=3（钟大小为11）
8.8.1.4.3. 阿诺德的PPN=（2^9=512,512 mod 11）= 6（钟大小为11）
8.8.1.5. 你和阿诺德各自单独获得对方的公开–私人数字，再将其与自己的私人数字相混合
8.8.1.5.1. 共享密钥=其他人的PPN^私人数字 （钟大小）
8.8.1.5.2. 你的共享密钥=(6^8=1679616,1679616 mod 11)=4（钟大小为11）
8.8.1.5.3. 阿诺德的共享密钥=(3^9=19683,19683 mod 11)=4（钟大小为11）
8.8.1.6. 尽管你按照不同的顺序混合了各种成分，但你和阿诺德都使用了相同的成分，因此也得到了相同的共享密钥
9. RSA
9.1. 1978年
9.2. 罗纳德·李维斯特（Ronald Rivest）
9.3. 阿迪·沙米尔（Adi Shamir）
9.4. 雷奥纳德·阿德尔曼（Leonard M.Adlemen）
9.5. 20世纪70年代为自己的系统申请了专利，而他们的专利直到2000年年末才失效
10. 背后的故事
10.1. 英国政府在数年前就已经知道类似迪菲–赫尔曼密钥交换和RSA系统
10.2. 那些发明迪菲–赫尔曼机制和RSA的先驱是英国政府通信实验室GCHQ的数学家
10.3. 他们工作的结果被记录在内部机密文件中，直到1997年才被解密
到了这里，关于读改变未来的九大算法笔记04_公钥加密的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
![[XJTU计算机网络安全与管理]——第五讲公钥加密算法](https://imgs.yssmx.com/Uploads/2024/02/426597-1.png)
