前言:基变换在做图像压缩等计算的时候,经常用到。基变换和相似矩阵的定义也有非常密切的联系:基变换的本质就是变换了基向量的一个关联计算,在最小二乘的算法里面,通过选择正确的基可以将计算进行简化。
而正确的的特征向量和特征值的确定,又和本节的基变换互为相互印证的关系。
基变换的标准定义:
基变换的实质是, 将某向量空间中的元素v 由有序基 F[w1,w2...vn] v=x1w1+x2w2 +...xnwn的线性组合,表示成另一有序基E[v1,v2,...vn]即v=y1v1+y2v2+...ynvn的线性组合
文章来源地址https://www.toymoban.com/news/detail-471731.html
1基向量的来源
在二维向量空间有一个向量如下:

用单位基向量的缩放表示如下:【^i】和【^j】是单位基向量


我们可以隐含假设认为:

【案,坐标2,表示向右运动,坐标3表述向上运动,基向量的单位表征运动的快慢】
由此,我们有如下定义:

[3,2]被称为标准的坐标系下的向量,而【^i】和【^j】是这个标准坐标系的基向量
2 不同的基向量的由来
如果我们定义一组不同的单位基向量作为构成向量空间的基础,看看会发生什么?
例如:
我们在原来的向量空间,定义任意两个向量,b1,b2,并把它作为单位基向量:

【案,记住这个新的基向量在原有基向量空间的坐标后面要用到】
那么在这个新定义的坐标向量坐标系统里面,b1,b2变成了单位向量。
也就是原来的基向量[1,0]由[-1,1]代替了,而原来的基向量[1,0]由[2,1]这两个新的基向量分别代替了。
【我们先称呼这两个变换后的基向量简称为斜的基向量,变换后向量空间为斜的向量空间,以便于简化描述,这个斜向的向量空间,在参考视频里面又叫做詹妮弗的向量空间】


在这个新定义的斜坐标系统里面,隐含假设发生了变化:
方向和单位长度都变化了。
【案,注意为了对比向量坐标系统已经发生了变化,我们用平行四边形的网格背景表述新的向量坐标系统空间】
两个坐标系统,唯一相同的是可以拥有同一个原点:

这样,我们就构建了一个新的基向量的斜的坐标系统
3 基变换:
既然,构建了新的基向量坐标空间,那么,不同的坐标空间内,某一个空间内的向量如何在另外一个变换后的空间内找到位置呢?
比如:这个斜的基向量空间的[-1,2]向量,在我们原来标准的向量空间是哪个向量对应呢?


在斜的基向量空间,向量[-1,2]大致可以表述为下面这个图:

现在,我们加上斜的基向量在原向量空间的坐标位置:


【案,注意,关键的联系表述出现了,如下:】
我们在斜向变化后的向量空间取的任意向量[-1,2],他在原来的向量空间的坐标,应该是通过这样一个变换得到:
【案,解释一下为啥是下面这个计算公式:1 向量在向量空间的张成位置,就是通过他的坐标长度*单位向量所得。 2 我们现在乘的单位向量的值,是已经经过转变后到原来的正方形单位向量的向量空间的值,所以,出来的结果也是原来的向量空间的值,而不是斜的的向量空间】

【也就是通过上面这个乘积的变换,我们搞成了原来的坐标系】
【案,这里原视频解释不够细致,我们可以理解为向量之间的一种线性变化的关系和联系,而,这有点像点积的表达??】
也就是:我们得到了斜向坐标系下[-1,2]变成了我们坐标系下[-4,1]的对应向量。

这里就是用某个向量的特定坐标与他的基向量数乘然后相加:
而这就是矩阵的向量乘法:

矩阵的向量乘法,可以理解为应用一个特定的线性变换【矩阵的列,就是变化后的新的基向量,他乘以新的坐标系下的某个特定向量,得到,我们原来变换前的向量的位置和值】
再仔细考虑上面这个思想:
1 首先-特定向量是基向量的特点线性组合:

2 变换后的向量仍然是线性组合的,不过使用的是新的基向量
3 然后思考,这个变换是在两个不同的基空间进行:

并且,其实只是表述不同【类似于语言不同,表达的意思一样】
也就是【-1,2】在斜网格空间等价于【-4,1】在我们【原始】的空间的表述。
以上,我们完成了一个斜向空间【基向量不是单位向量的变更空间】内的一个矢量变换到之前我们的元素单位空间的例子。
====================================================================
那么,现在我们反过来呢?如果从一个原始的坐标系的向量坐标变换到斜向的坐标系下的坐标呢?
在第一节里面,我们有如下的一个向量:
用单位基向量的缩放表示如下:【^i】和【^j】是单位基向量


步骤1:变换后的基向量是什么?
我们设定,变换后我们的两个基向量分别是[2,1],[-1,1]
步骤2:原始 --》斜向的变化矩阵
于是从这两个基向量构成的,我们称为斜的向量空间,变换到之前元素的坐标用的变换矩阵:就是

步骤3:斜向的变化矩阵 --》原始
这个显然是步骤2的逆变换,而,一个变换的逆变换是一个新的变换,他是什么呢?

经过计算应该是右边这个矩阵:
步骤4,现在我们把元素坐标下的向量,逆变换到斜向的向量空间。

【逆变换的矩阵乘法如上】

这就是斜向向量空间里面和之前的[3,2]对应的那个向量。
推而广之:

右边的式子,也可以用逆变换,或者说逆矩阵表述为:



举例:
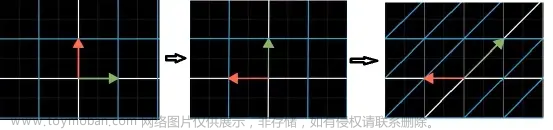
1 一个90度的选择的坐标变换:
1.1 从原始坐标系统来理解:

用坐标变换,跟踪一下,变换后的坐标:

并把这个坐标作为矩阵的列:
这里我们理解为:

1.2 从斜的坐标空间来理解:
在斜向坐标系下有一个任意的向量:

我们通过基变换矩阵把他变换从我们原始的坐标系下的向量:

然后,我们再左乘,【90度旋转的变换矩阵】


【注意,这样变换的结果就是我们原来坐标系下,变化后的向量了】
如果我们闲着蛋疼,想把这个向量再边到斜向坐标系里面去,那么,只需要再左乘一个原来变换的逆矩阵,就可以了。


【OK,如果我们把这些变换都放到一起,如上,我们就实现了一个在斜向的向量空间下,对任意给定的斜向坐标系下的向量的一个90度的翻转变换】
然后,我们可以计算和化简这个变换,最后得到,

【注意,这里变换的矩阵分别出现了两次,一次是左乘的逆矩阵,一次是右乘的矩阵】

于是可以拿来和任意一个想要翻转的向量来相乘,实现变换【在斜向向量空间下】
本例,这个给出的要变换的向量是[1,2]
于是有:如下的左乘计算完成了这个变换,

推而广之:

M就是你要的变换,A则表示你的数学上或者说空间上的转移作用的转移矩阵。
【案,转移矩阵必定为非奇异的(满秩)的】
推而广之,上面的式子其实也是一个相似变化的定义很像:

再推而广之,
矩阵的化简,可以通过对角化来实现矩阵化简。而能否对角化,又是通过判断和特征向量有关。这一个概念的联系,应该在下一节会介绍。
2 基变换公式
【案,这里从数学角度再推导一下】
【基变换公式,就是基向量变换公式】
在说明之前,先预备一下知识:就是向量的线性表出的三种形式记号:

【案,形式3 ,和形式1都是向量的线性表述的写法】
如果推而广之到一个多维的向量组,那么有,


3 坐标变换公式
例题1:
理解了上述概念后,我们来做一道实际的例题,加深一下印象:

【案,这里有序基就是可以看出是一个基向量】

【这个例子,将两个有序基的转换表述出来,这里表述了用有序基[1,x,x^2]来表述有序基[1,2x,4x^2-2],这里基向量就是有序基,而这样就可以写出他对应的系数矩阵,注意这里是按照行的方式写,不影响结果】
【也就是完成了一个从[1,2x,4x^2-2], 到 [1,x,x^2]的转换】

而,反过来,

计算得到他的逆矩阵为:

然后,我们给的P3任意一个p(x),【也就是我们前面讨论的,一个向量空间的某一个任意向量】

【案,注意这里这个通用方程的系数[a,b,c],就是我们要给出的任意向量的值】
求他对应于:【基向量】 的坐标,
的坐标,
按照之前讨论,我们只需要用变换矩阵去左乘给出的任意向量,就可以完成这个向量的空间变换,也就是,


这个就是基于新的基向量的方程形式。
例题2,

上面推导如下:


由此,


由此

所以,

所以,

如果,换成基向量的变化,也就有:





词汇:
1implicit assumptions 隐含假设
2change of basis matrix 基变换矩阵
参考:
【官方双语/合集】线性代数的本质 - 系列合集_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1ys411472E?p=13
(46条消息) 关于基变换_weixin_33725807的博客-CSDN博客https://blog.csdn.net/weixin_33725807/article/details/86252992?spm=1001.2101.3001.6650.5&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-5.no_search_link&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-5.no_search_link(57条消息) 线性代数【10】 相似矩阵_山云的专栏-CSDN博客https://dimensionspacex.blog.csdn.net/article/details/121491943
(46条消息) 基变换和坐标变换_大哉数学之为用-CSDN博客_基变换和坐标变换https://blog.csdn.net/Daniel_tanxz/article/details/89135594?spm=1001.2101.3001.6650.9&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-9.no_search_link&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-9.no_search_link
旋转矩阵(Rotation Matrix)的推导及其应用 - meteoric_cry - 博客园 (cnblogs.com)https://www.cnblogs.com/meteoric_cry/p/7987548.html文章来源:https://www.toymoban.com/news/detail-471731.html
到了这里,关于【线性代数】20 基变换,基变换公式,坐标变换公式的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!