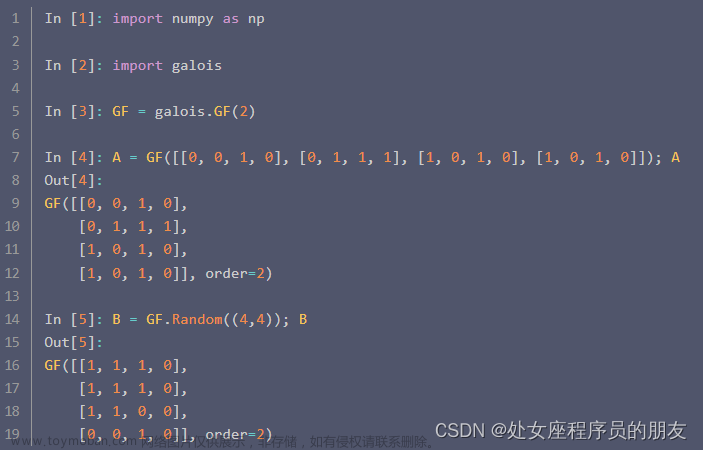
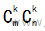1.行秩与列秩
前序:
所以,行秩与列秩的关系为,一般情况下总是相等,这也是为什么,
我们既可以:
通过行变换也可以通过列变换求秩。
通过对行的初等列变换,以及对列的初等行变换求极大无关组,都是可以的。文章来源:https://www.toymoban.com/news/detail-472109.html
2.行满秩与列满秩
①行满秩与列满秩。
若矩阵秩等于列数,称为列满秩。
若矩阵秩等于行数,称为行满秩。
②即是行满秩又是列满秩一定是方阵。
既是行满秩,又是列满秩则为n阶矩阵即方阵,所以如果是方阵,则行满秩与列满秩是等价的。
③行满秩与列满秩没有必要联系。
行满秩与列满秩是两个基本概念,两者不具有严格关系。
在一个矩阵中,虽然行向量的极大线性无关组数等于行数,但是列向量的极大无关线性组却不等于列向量数。只有行列式不为0的方阵,二者才相等。
④注意与行秩列秩区分。
在一个矩阵中行秩一般等于列秩=秩,但是我这里说的是行秩,列秩,而不是行满秩,列满秩不要弄混了。文章来源地址https://www.toymoban.com/news/detail-472109.html
到了这里,关于矩阵行秩与列秩的关系。的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!