文章目录
- 一、动态规划简介
- 二、动态规划求解步骤
-
三、动态规划典型应用
- 数字三角形问题
- 最大子段和问题
- 0-1背包问题
-
四、最长公共子序列问题
- 动态规划求解
- 五、总结
前言
算法语言--java语言
一、动态规划简介
动态规划算法通常用于求解具有某种最优性质的问题。动态规划与分治算法类似,其基本思想也是将待求解的问题分解成若干个子问题,再把子问题合成一个最优解。
动态规划与分治法的区别:
分治法子问题相互独立,动态规划子问题不相互独立。
动态规划问题应具备两个基本要素:
1、最优子结构性质,2、子问题重叠性质
二、动态规划求解步骤
动态规划算法适合用于求解最优化问题,通常可按以下步骤来设计:
(1)分析最优子结构性质
(2)递归地定义最优值
(3)以自底向上的方式计算出最优值
(4)根据计算最优值时得到的信息,构造最优解
三、动态规划典型应用
1、数字三角形问题
有一个群岛,共分为若干层,第1层有一个岛屿,第2层有2个岛屿,......第n层有n个岛屿。每个岛上都有一块宝,其价值是一个正整数(图中圆圈中的整数)。
寻宝者只允许从第一层的岛屿进入,从第i层的岛屿退出,不能后退,他能收集他所经过的所有岛屿上的宝贝。但是,从第i层的岛屿进入第i+1层的岛屿时,有且仅有有2条路径。你的任务是:对于给定的群岛和岛上宝贝的价值,计算一个寻宝者行走一趟所能收集宝贝的最大价值。

问题分析:
这个问题抽象成三角形问题,从顶部出发,从顶至底选一条路径,使该路径经过的数字总和最大。
本题采用贪心算法就无法找到真正的最大和。当从顶部向下,使用贪心算法时,路径上的数字和为:9+15+8+9+10=51。而真正的最大和为9+12+10+18+10=59。因此本题不能使用贪心算法求最大和。

视频讲解如下链接:
https://www.bilibili.com/video/BV1Z94y1D7CA/?spm_id_from=333.337.search-card.all.click&vd_source=4db006022c06ce1bdafdbea04cd95cb0
动态规划法求解:
public class Main {
public static void main(String[] args) {
int n = 3;
Scanner in = new Scanner(System.in);
int[][] data = new int[n+2][n+2];
for (int i=1;i<=n;i++){
for (int j =1;j<=i;j++){
int temp = in.nextInt();
data[i][j] = MaxNum(data[i-1][j-1],data[i-1][j])+temp;//本层数加上一层两者最大的数
}
}
//最底层的列比较大小
int result = 0;
for (int i=1;i<=n;i++){
if (result<data[n][i]){
result = data[n][i];
}
}
System.out.println("最大结果为:"+result);
}
static int MaxNum(int a,int b){
if (a>b){
return a;
}else {
return b;
}
}
} 运行如下:
2、最大子段和问题
最大子段和问题:给定n个元素的整数列(可能为负整数)a1,a2......an。求其和的最大值。
例如当(a1,a2,a3,a4,a5,a6)= (-2,11,-4,13,-5,-2),最大子段和为11-4+13=20
现在求当(a1,a2,a3,a4,a5,a6)=(11,-2,-4,13,-5,-2),最大子段和为多少?
问题分析:
动态规划求最大子段和比分治算法要简单得多!
如子段和是大于0,则加上下一个数,如果小于0,则直接舍弃前面,加下一个数。
代码如下:
public class Main {
public static void main(String[] args) {
int data[] = {11,-2,-4,13,-5,-2};
int max = MaxSum(data,6);
System.out.println("最大子段和为:"+max);
}
static int MaxSum(int data[],int n){
int a = 0;
int max = 0;
for (int i = 0; i < n; i++) {
if(a>0){
a = a+data[i];//做累加
}else{
a = data[i];//直接舍弃前面
}
if(a>max){
max = a;
}
}
return max;
}
}运行如下:

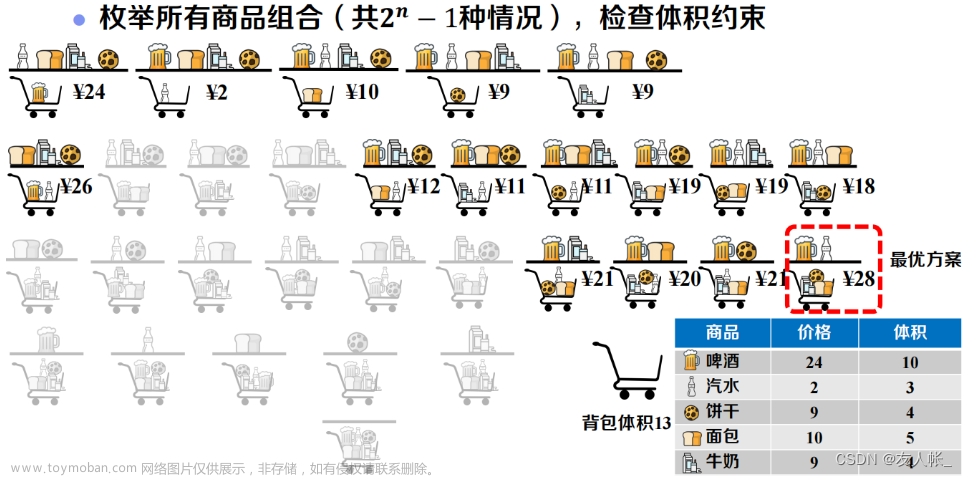
3、 0-1背包问题
给定一个物品集合S = {1,2,3...,n},物品i的重量是wi,其价值是vi,背包的容量为W,即最大载重量不能超过W。在限定的总重量W内,我们如何选择物品,才能使物品的总价值最大。
| W=5 | 物品1 | 物品2 | 物品3 | 物品4 |
| 重量w | 2 | 1 | 3 | 2 |
| 价值v | 12 | 10 | 20 | 15 |
填写最优值解析:
解法归纳:
一、如果装不下当前物品,那么前n个物品的最佳组合和前n-1个物品的最佳组合是一样的。
二、如果装得下当前物品。
假设1:装当前物品,在给当前物品预留了相应空间的情况下,前n-1个物品的最佳组合加上当前物品的价值就是总价值。
假设2:不装当前物品,那么前n个物品的最佳组合和前n-1个物品的最佳组合是一样的。
选取假设1和假设2中较大的价值,为当前最佳组合的价值。
| 物品\背包容量 | 0 | 1 | 2 | 3 | 4 | 5 |
| 物品1:w=2 | 0 | 0 | 12 | 12 | 12 | 12 |
| 物品2:w=1 | 0 | 10 | 12 | 22 | 22 | 22 |
| 物品3:w=3 | 0 | 10 | 12 | 22 | 30 | 32 |
| 物品4:w=2 | 0 | 10 | 15 | 25 | 30 | 37 |
讲解视频:
【动态规划】背包问题_哔哩哔哩_bilibili
代码实现:
public class Text {
public static void main(String[] args) {
int w[] = {0,2,1,3,2};//物品重量
int v[] = {0,12,10,20,15};//物品价值
int bagMax = 5;//背包大小
int dp[][] = new int[5][6];//背包问题表格
for (int i=1;i<=4;i++){
for (int j=1;j<=bagMax;j++){
if(j<w[i]){
dp[i][j] = dp[i-1][j];
}else {
dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
}
}
}
//表格的打印
for (int i = 0;i<5;i++) {
for (int j =0;j<6;j++){
System.out.print(dp[i][j]+"\t\t");
}
System.out.println();
}
}
static int max(int x,int y){
if (x>y){
return x;
}else {
return y;
}
}
}运行如下:

四、最长公共子序列问题
1、问题描述:
著名的最长公共子序列问题,即寻找序列间最大或最多公共点的问题。最长公共子序列算法的主要作用是找出两个序列中最长的公共子序列,是一种非常基础的算法,被广泛应用于程序相似性对比、图形相似处理解、计算生物学等方面。
生物学家常常利用该算法进行基因序列对比,由此推测序列的结构、功能和演化过程。
最长公共子序列问题的定义为:设有两个序列X[1:m]和Y[1:n],需要寻找它们之间的一个最长公共子序列。
例如,假设我们有如下两个序列:
X:A B C B D A B
Y: B D C A B A
则X和Y的最长公共子序列的长度为:4
则X和Y的一个最长公共子序列为:B C B A
2、动态规划求解
利用动态规划寻找最长公共子序列的步骤如下:
(1)先寻找最长公共子序列的长度。
(2)再通过算法从而获得最长公共子序列
根据题目得到的递推公式为:

3、代码实现
public class Text {
static final int max = 100;
static int[][] c = new int[max][max];
static int[][] b = new int[max][max];
//长度的动态规划算法
public static int LCSLength(int m,int n,char x[],char y[]){
for (int i=1;i<=m;i++){
c[i][0] = 0;
}
for (int i=1;i<=n;i++){
c[0][i] = 0;
}
for (int i = 1; i <=m; i++) {
for (int j = 1; j <=n; j++) {
if(x[i]==y[j]){
c[i][j] = c[i-1][j-1]+1;
b[i][j] = 1;
}else if(c[i-1][j]>=c[i][j-1]){
c[i][j] = c[i-1][j];
b[i][j] = 2;
}else if(c[i-1][j]<c[i][j-1]){
c[i][j] = c[i][j-1];
b[i][j] = 3;
}
}
}
return c[m][n];
}
//打印最长子序列
public static void LCSL(int i,int j,char x[]) {
if(i==0||j==0) {
return;
}
if (b[i][j]==1) {
LCSL(i - 1, j - 1, x);
System.out.print(x[i]);
}else if (b[i][j]==2){
LCSL(i-1,j,x);
}else{
LCSL(i,j-1,x);
}
}
public static void main(String[] args) {
char x[] = {'0','A','B','C','B','D','A','B'};
char y[] = {'0','B','D','C','A','B','A'};
int max = LCSLength(x.length-1,y.length-1,x,y);
System.out.println("最长公共子序列的长度为:"+max);
System.out.print("最长公共子序列为:");
LCSL(x.length-1,y.length-1, x);
}
}
五、总结
动态规划和分治法十分类似,主要区别为:
分治法子问题相互独立,动态规划子问题不独立。
可以使用一个表来记录所有已解的子问题的答案。
拥有最优子结构性质和子问题重叠性质的题考虑用动态规划求解。文章来源:https://www.toymoban.com/news/detail-472199.html
动态规划问题需要多思考多做题才能熟能生巧,得慢慢看视频慢慢懂。文章来源地址https://www.toymoban.com/news/detail-472199.html
到了这里,关于算法分析与设计--动态规划的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!