泊松分布



连续性随机变量概率密度
概率密度积分求分布函数,概率密度函数积分求概率,分布函数端点值相减为概率






均匀分布




正太分布标准化

例题

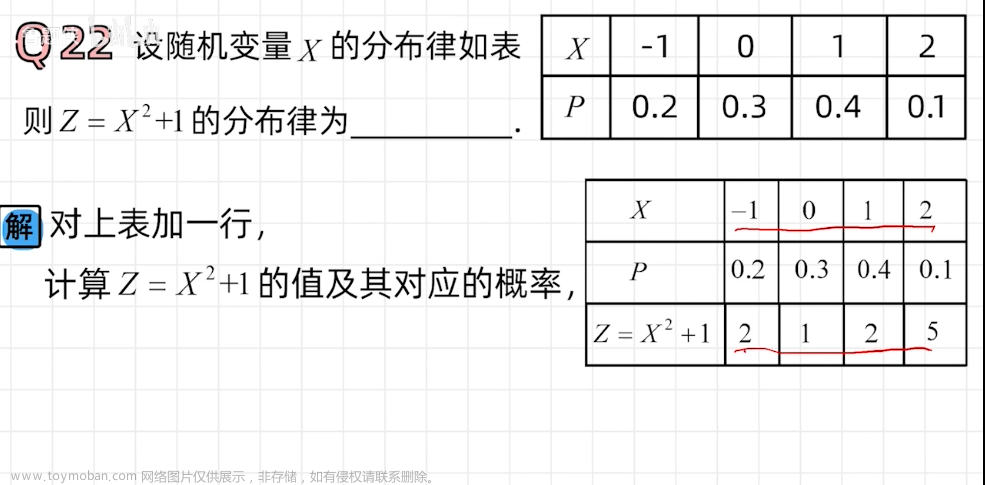
离散型随机变量函数的分布


概率密度求概率密度
先积分,再求导


例题




二维离散型随机变量的分布
联合分布律

离散型用枚举法



二维随机变量的的分布

例题



例题2:



离散型随机变量函数的分布





连续性随机变量函数的分布



正太分布可加性



例题2


数学期望



方差和标准差



例题2



常见的随机变量的期望和方差




协方差和相关系数






二维离散型随机变量期望与方差的计算






中心极限定理

将二项分布近似为正太分布
先根据二项分布求出期望和方差,然后根据期望与方差求u和C塔的平方



三大分布

例题




矩估计





极大似然估计
离散型




连续性

假设检验




-kOqQth5a-1640708495514)]
连续性
假设检验



 文章来源:https://www.toymoban.com/news/detail-472688.html
文章来源:https://www.toymoban.com/news/detail-472688.html
 文章来源地址https://www.toymoban.com/news/detail-472688.html
文章来源地址https://www.toymoban.com/news/detail-472688.html
到了这里,关于概率论与数理统计期末复习的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!