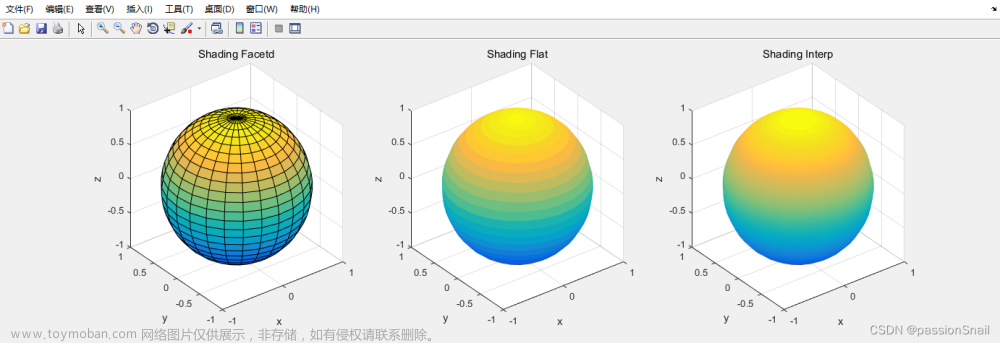
matlab绘制三维图中，最常见的是三维曲线图和三维曲面图
三维曲线图比较简单函数命令为plot3，已经详细介绍过，具体请见Matlab三维绘图------三维曲线图
三维曲面图的不同类型及对比
三维曲面图又分为三维网面和三维网格面图，其原理相似只是调用格式不同而已。总结如下：
plot3(x,y,z);%绘制数据的三维曲线图
mesh(x,y,z); %绘制数据的三维网格面图
surf(x,y,z); %绘制数据的三维网面图
meshc(x,y,z);%绘制数据的三维网格面图，并添加等值线
surfc(x,y,z);%绘制数据的三维网面图，并添加等值线
meshz(x,y,z);%绘制数据的三维网格面图，并添加等值线
[X,Y]=meshgrid(x,y);分别产生两个1、以向量x为行，向量y为列的矩阵，2、并且向量x的长度为新矩阵的列数，y的长度为新矩阵的行数 的新矩阵X和Y.
上面：[X,Y]=meshgrid(x,y)在绘制三维曲面图中非常重要，在用方程绘制曲面图中常用。在这里不赘述，详细介绍可见前文，请点击下面超链接。
比如向量x=[1,2,3],向量y=[4,5],[X,Y]=meshgrid指令的作用是分别产生两个1、以向量x为行，向量y为列的矩阵，2、并且向量x的长度为新矩阵的列数，y的长度为新矩阵的行数 的新矩阵X和Y.
在这里即为两行三列。所以：
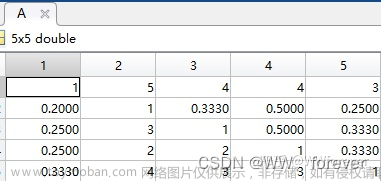
X=
1 2 3
1 2 3
Y=
4 4 4
5 5 5
关于[X,Y]=meshgrid指令的作用已详细讲过，具体可见Meshgrid用法简介
关于mesh(x,y,z)、surf(x,y,z)、meshc(x,y,z)、surfc(x,y,z)、meshz(x,y,z);这几个函数的区别，通过绘制高斯矩阵的曲面来看看
z=peaks(40);
mesh(z)
surf(z)
meshc(z)
surfc(z)
meshz(z)
将这些图分别绘制在一张figure上也非常简单，仍然是用到多重子图subplot指令：
z=peaks(40);
subplot(2,3,1);
mesh(z);
subplot(2,3,2);
surf(z);
subplot(2,3,3);
meshc(z);
subplot(2,3,4);
surfc(z)
subplot(2,3,5);
meshz(z)
总结：mesh是网格，surf是网面。网格绘出的三维图就像是渔网一般一格一格的。网面绘出的三维图是曲面的，上面没有格，至于线是辅助线。mesh(z)和surf(z)则是加了等值线，相当于那些值相等，就用圈圈做以标记。meshz(z)是加了一个零平面作为参考。
用方程绘制三维曲面图
举几个不同的例子来说明
例1:
x在[0,2pi],y在[0,2pi],作三维曲面图z=cos(x)+sin(y)
x=(0:0.01:2*pi);
y=x;
[X,Y]=meshgrid(x,y);
z=cos(X)+sin(Y);
mesh(X,Y,z)
注：通常在确定向量x,y的基础上，使用命令meshgrid生成新的矩阵数据[X,Y]，再输入函数z=f(x,y,z)，最后用mesh或surf指令生成三维曲面图。
如果不用meshgrid生成矩阵的话会有如下错误：
例2：
绘制如下方程的三维曲面图:
x=(-7.5:0.01:7.5);
y=x;
[X,Y]=meshgrid(x,y);
R=sqrt(X.^2+Y.^2);
Z=sin(R)./R;
mesh(X,Y,Z)
通过meshgrid指令将向量x和y，分别生成了矩阵X、Y.那么在以上代码中
R=sqrt(X. ^2+ Y.^2)以及Z=sin（R)./R中的加了.的原因是什么呢？
这是因为在变量运算里有以下几个基本规则：
a.*b %矩阵a和矩阵b中各个元素相乘
a.*b.*c %矩阵a,矩阵b和矩阵c中各个元素相乘
a.^2 %求取矩阵a中各个元素的平方
a./b %矩阵a中各个元素除以矩阵b中的各个元素
a.\b %矩阵b中各个元素除以矩阵a中的各个元素
因而先通过meshgrid指令将向量变成矩阵X和Y，再通过上述指令：
x的平方就是a.^2 即：X.^2，以及y的平方： Y.^2 ，而sin（R)/R即a./b ， 即：sin（R)./R
以上了解了之后用方程绘制三维曲面图就非常简单了，再来一个例子：
x=(-3:0.01:3);
y=(-4:0.01:3);
[X,Y]=meshgrid(x,y);
Z=X.*exp(-(X.^2+Y.^2));
mesh(X,Y,Z)
文章来源：https://www.toymoban.com/news/detail-472853.html
theta=(-pi:0.05:4*pi);
x=cos(theta);
y=sin(theta);
[X,Y]=meshgrid(x,y);
z=abs(cos(X.*3)).*exp(-abs(theta/3));
mesh(X,Y,z)
文章来源地址https://www.toymoban.com/news/detail-472853.html
到了这里，关于MATLAB三维绘图---三维曲面图的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
