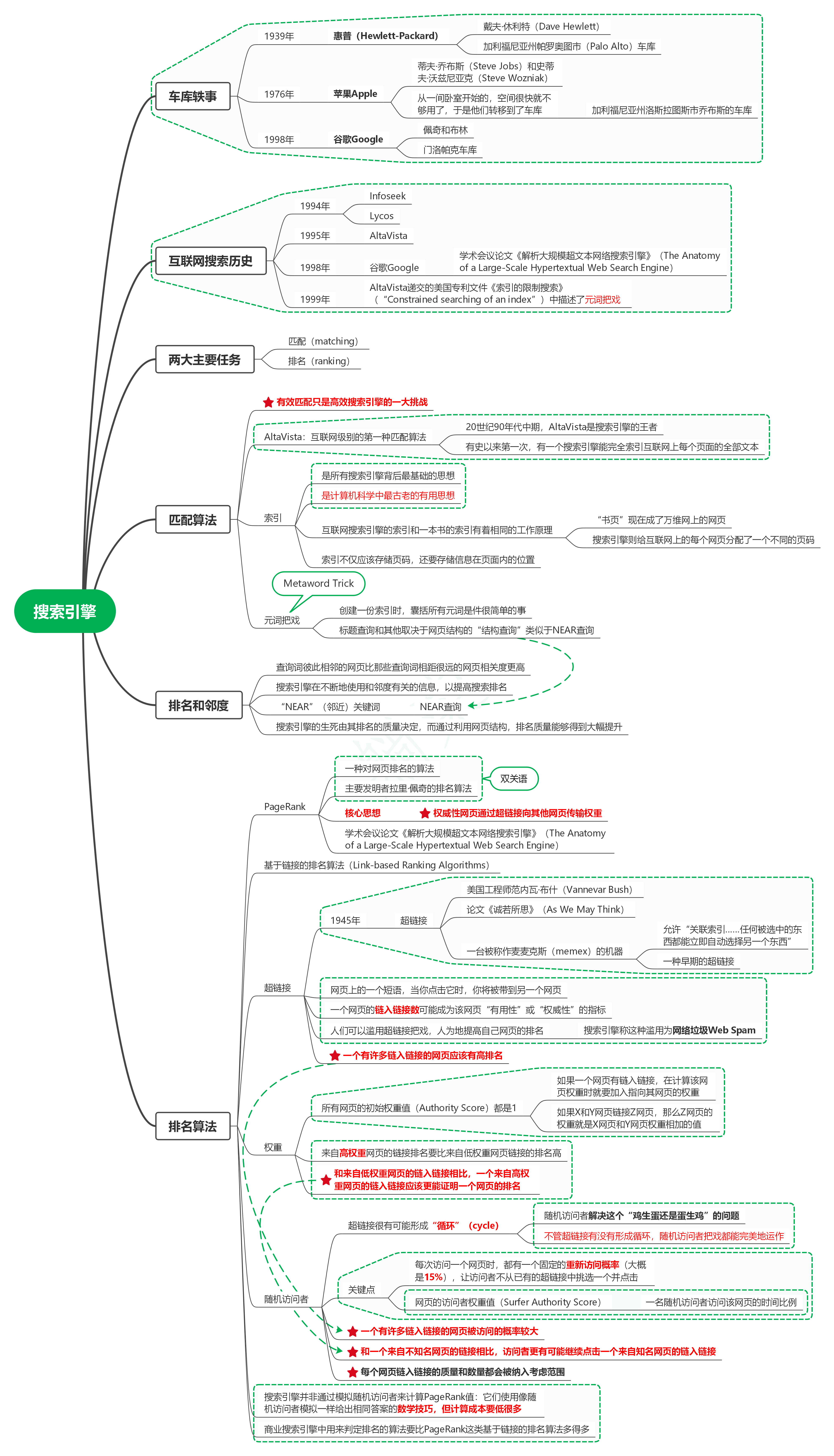
1. 数字签名”（Digital Signature）
1.1. 单词数字化（digital）意味着其“由数字字符串组成”
1.2. 任何数字化的东西都能被拷贝
1.3. “签名”的全部意义在于能被读取，但不能被除了作者的任何人拷贝（也就是伪造）
1.4. 软件签名是数字签名最明显的应用
1.5. 一个数字签名同时依赖一个只有签名者知道的秘密和被签署的消息
1.6. 没有数字签名，我们所知的互联网就不会存在
2. 用挂锁签名
2.1. 上锁的箱子就是文件的签名
2.1.1. 加锁的箱子透明，这一机制的效果就会更好
2.1.2. 数字签名提供的是可靠性，而非隐秘性
2.2. 一个受信第三方
2.2.1. 参与者不是给银行一份签名，而是给银行一把能打开自己挂锁的实体钥匙
2.3. 如果弗朗索瓦丝需要证明拉维写了欠条，她只要和一些目击证人把锁箱带到银行，在银行用拉维的钥匙打开箱子即可。
2.4. 挂锁能打开就证明只有拉维能对箱中内容负责，而箱中正好是弗朗索瓦丝能试图验证的那份文件
3. 用乘法挂锁签名
3.1. 上锁或开锁动作将由钟算乘法（Multiplication in Clock Arithmetic）代表
3.2. 计算机使用的钟大小非常大——钟大小长度基本在数十或数百位数
3.3. 示例
3.3.1.
文章来源：https://www.toymoban.com/news/detail-473049.html
3.3.1.1. 钟大小为11的乘法表
3.3.2. 拉维选择11作为钟大小，选择6作为挂锁
3.3.3. 拉维的消息是“5”
3.3.4. “上锁”消息会是6×5，通过钟算得到结果为8
3.3.5. 最终结果“8”就是拉维给原始消息的数字签名
3.3.6. 欧几里得算法得到钥匙为2
3.3.7. 将8用钟算乘以钥匙2，就能得到结果5
3.3.8. 拉维可以公开宣布自己选择的钟大小和钥匙值
3.4. 数字挂锁是私有的，而数字钥匙和钟大小则是公开的
3.4.1. 挂锁值是私有的（或秘密的）
3.5. 乘法方法的缺陷
3.5.1. 用于从挂锁生成钥匙的同样把戏——基本上是指欧几里得算法——能非常完美地逆向运行：同样的技术能让计算机生成与已有钥匙值对应的挂锁值
3.5.2. 敌人无须依靠暴力破解就能逆转过程
3.5.2.1. 欧几里得算法也能根据钥匙值计算出挂锁值，而这一算法要比暴力破解高效得多。这也是乘法方法被认为不安全的原因
4. 用指数挂锁签名
4.1. 著名数字签名机制RSA
4.2. 示例
4.2.1.
文章来源地址https://www.toymoban.com/news/detail-473049.html
4.2.1.1. 钟大小为22时n的三次方和七次方的值
4.2.2. 拉维选择3作为挂锁值
4.2.3. 消息是“4”，签名是“20”
4.2.4. 钥匙值为7
4.2.5. 20^7钟算结果为4，为原始消息
4.3. 通过试错总有可能算出某人的挂锁值
4.3.1. 暴力破解（Brute Force）
4.3.2. 我们知道挂锁值要小于钟大小，因此我们可以简单地逐一尝试所有可能的挂锁值，直到找到一个能生成正确签名的挂锁值
4.4. 诀窍是RSA机制使用绝对大的钟大小
4.4.1. 数千位数长
4.4.2. 现存最快的超级计算机，也要花数万亿年才能尝试所有可能的挂锁值
4.5. 对敌人是否能用某种方法计算出挂锁值不感兴趣
4.5.1. 想知道敌人是否能足够高效地这么做，从而造成实际威胁
4.5.1.1. 发明一种高效的分解因子算法只会破坏类RSA机制
4.6. 钟大小的两个素数因子仍然保密
到了这里，关于读改变未来的九大算法笔记05_数字签名的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
