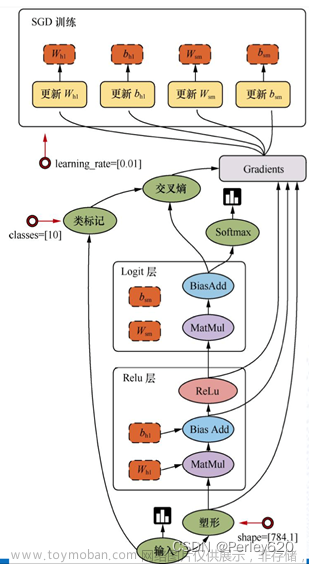
这里用比较简单的语言和思路(自认为)为大家介绍一下BP神经网络的基础架构和流程。不会写数学推导以及一些绕来绕去的概念,尽可能让大家一看就懂怎么回事。因此这篇文章适合初学者,帮助顺清整个流程。
有一点点基础的同学直接看最后一张图,看看最后那两个式子应该就懂了!
首先看个图,以下讲解以这个神经网络结构为例。

我们应该明确构建神经网络的目的是: 通过输入X1与X2,经过一些操作得到一个y。
中间这些神经元构成的结构就是神经网络。
首先明确一下这个流程里有哪些东西。请看下图。

第一列两个神经元称为输入层i,中间三个神经元称为中间层j,最后一个神经元称为输出层k。
除了输入层,每个神经元都自带一个偏置b,且自带一个激活函数f。每个神经元之间的连线称为权重w,图中加粗的三根线表示输入层第一个神经元与中间层三个神经元之间的权重w。其他没写的线也同理。
总结一下,目前所有出现的东西有:
输入值X,神经元之间的权重w,每个神经元自带的b,每个神经元自带的激活函数f。
后面还会出现u、y。
我们用一个最简单的结构来梳理流程:

首先X1给到输入层神经元,然后用得到一个u,这个u经过激活函数f会变成y。此时中间层神经元就有值了,值为y。

输出层的值也这样算。算得到一个u,u经过激活函数f得到y,这个y就是最终结果Y。注意这里的b和f不一定和上一个神经元的b、f一样,每一个神经元的b、f都是可以不一样的。
通式为:
所有神经元都按照这个流程算,输入层神经元获取x就可以往后算,中间层神经元的x就是上一层神经元算出来的y,输出层神经元的x就是中间层神经元算出来的y。
我们看这个红色的神经元,想要算这个神经元的值怎么算?

文章来源:https://www.toymoban.com/news/detail-473100.html
这样就算出来红色神经元的值为y,其他神经元同理。文章来源地址https://www.toymoban.com/news/detail-473100.html
到了这里,关于BP神经网络基础架构及流程(简单易懂版)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!