引入：曲边梯形面积
a和b中两点插入n个点，a=x0<x1<x2...xn=b，产生n-1个小片段x1-x0， x2-x1......
取n个区间内某点的函数值，y0，y1，y2...yn
产生多个小长方形面积，s=x*y
取
为x1-x0到xn-xn-1的最大值
曲边梯形面积=长方形的面积求和和当
趋近于0时，又叫从a到b的f（x）定积分
定积分：
定义：在有界函数在[a,b]插入任意分点,分成任意区间，在区间内任意一点的函数值
a为下限，b为上限，从下限到上限定积分
只和f（x），[a,b]有关，与积分变量无关
可积的条件：只有连续，或者有界有限个间断点
几何意义：在区间ab函数图像与x轴的形成的面积
定积分的正负：
f（x）大于0，定积分结果大于0
小于0，结果小于0
有正有负， 结果未知
理解：
对一个表达式就极限，结果为一个常数。
注意：1.积分上下限就是积分变量的范围
2.与积分变量无关的变量的数可以往外提
定积分近似计算：
1.用矩形的面积来近似：关键就是矩形的高度即某点的函数值
2.用梯形近似：无数个梯形面积求和
3.抛物线方法：取高度y1，y2，y3.....模拟出一个抛物线的方程，再用积分求出抛物线和x轴形成的阴影面积（这不就是用抛物线直接拟合原曲线吗，再对抛物线求定积分吗？）
定积分性质：
性质1，2
（1）直线的空间为0
性质3
和不定积分性质相同
性质4
与b，c大小无关，a<b,a<c，画图理解
函数是y=1，围成的面积就是（b-a）*1
推论1
f（x）围成的面积大于g（x）
推论2
左项围成的面积正负抵消，使得总使得左项小于等于右项
M，m为某个函数值的y值，就是以b-a的底，不同函数值为高的长方形和实际面积比较
定积分中值定理：
以b-a为底的长方形，面积等于曲线梯形，由上一个定理可知，曲线的面积在m*（a-b）和M*（a-b）之间，必然存在一点的
*（a-b）刚好等于面积
此时
为平均值
微积分的基本公式：
从T1到T2的行驶的距离（速度是变化的）
积分上限函数：固定下限，上限是变的
对积分上限函数求导：
就是定积分式子，定积分的导数是被积的函数。
理解：把f（x）看成速度，x看成时间，路程对时间求导就是瞬时速度，就是f（x）
积分下限函数求导：将它变成上限是x的函数乘-1
定积分复合函数求导：
上限是符号函数：
上下限都是复合函数：
先把上限代进去，对上限求导，再把下限代进去对下限求导
牛顿-布莱公式：
F（x）是f（x）原函数即F'(x)是f（x）。
x的范围[a,b]
从不定积分角度来看，就是在时间a到b中，某个函数的导数是速度，
这个函数就是以时间为自变量，行走的路程为应变量F（x）
由时间a到b的路程就等于F（b）-F(a)
作用：求定积分可以用不定积分，先代上限，再代下限
定积分换元法：
1.引入换元函数
2.上下限也改变
3.考虑奇偶性
周期函数：
反常积分：
无穷限的反常积分：
上，下，上下限取无穷
依然用牛顿原则，把a代成无穷
无界函数的反常积分：
趋于无穷的点：瑕点
有瑕点的函数叫无界函数
b为瑕点，函数在的右侧有定义
总结：实际上就是改一种形式
计算出来的结果可能为无穷
瑕积分的欺骗性：
忽略原函数的瑕点，只看上下限
如果有瑕点要注上下限分开
瑕积分换元：单调函数
伽马函数:
定义：
1. 
2.
定积分应用：
元素法：举了几个列子
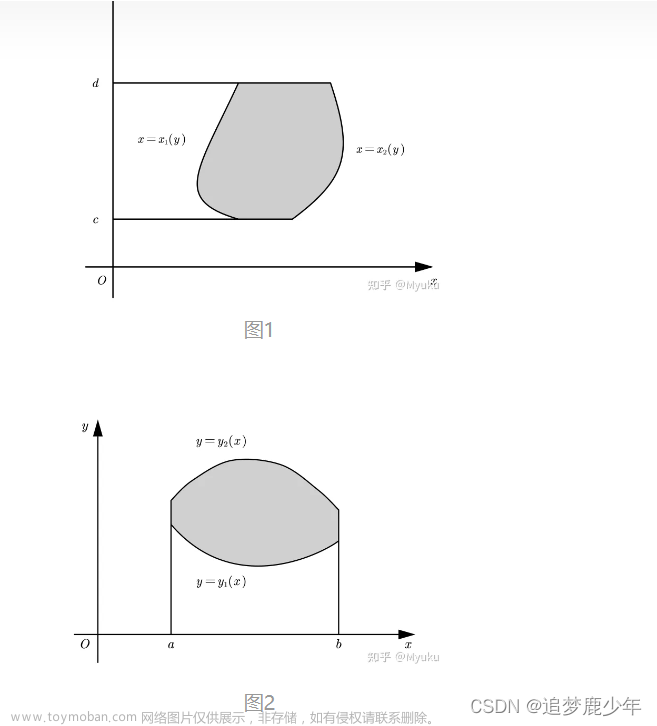
平面图形面积：
理解：把f（x）为一条线，许多条线密密麻麻凑成图形（更准确说是宽趋近于0），上面公式表示x从a到b的面积求和
1.x型区域：以x自变量
2.y型区域：以y为自变量
1.面积是不变的，以谁为自变量都可以
2.两函数有交点会有抵消要，分开求
3.减出来是负的也无所谓，取绝对值就行
实际上：应为四条线，两条圈定图型，两条限定范围
极坐标求面积：
p为弧线长，a为半径
大体和求平面图型一个思路。
取一小部分近似看成扇形，半径为p
求旋转体体积:
体积等于可以分为高趋近于0的许多给薄面（积分存在某个东西可以突破线性相关的原则）
求出很多个横截面的面积求和，横截面面积随着高变化而不断变化
1.绕x轴旋转，绕y轴旋转
定积分求弧长：
用弧上两点的连线来表示：
取极小的x加和极小的y
文章来源地址https://www.toymoban.com/news/detail-473179.html
极坐标：
文章来源：https://www.toymoban.com/news/detail-473179.html
定积分：物理应用……
到了这里，关于高数：定积分的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
